(答案)如皋市2024届高三1月诊断测试数学参考答案(1)_2024年4月_01按日期_6号_2024届新结构高考数学合集_新高考19题（九省联考模式）数学合集140套

如皋市 届高三 月诊断测试
2024 1
数学参考答案
2024.01
一、选择题：本题共8小题，每小题5分，共40分.
题号 1 2 3 4 5 6 7 8
答案 D B B A D A A A
二、选择题：本题共3小题，每小题6分，共18分.全部选对得6分，部分选对得3分，有选错得0分.
题号 9 10 11
答案 ACD BCD ABC
三、填空题：本题共3小题，每小题5分，共15分.
题号 12 13① 13② 14
答案 9 6 16 3 49
a 0或a 
8 3 27 13
四、解答题：本题共5小题，共77分.解答时应写出文字说明、证明过程或演算步骤.
15. （13分）
1 3 a 1 3
（1） f(x) alnx  x1，则 f(x)   ，
2x 2 x 2x2 2
又 f(1) 0，故可得a20，解得a 2；
1 3 (3x1)(x1)
（2）由(1)可知， f(x)2lnx  x1， f(x)  ，
2x 2 2x2
1
令 f(x) 0，解得x  ，x 1，
1 3 2
1 1
又函数定义域为(0,)，故可得 f(x)在区间(0, )和(1,)单调递减，在区间( ,1)单调递增.
3 3
1
故 f(x)的极大值为 f (1)  0， f(x)的极小值为 f( ) 22ln3.
3
16. （15分）
3 23 3 213 1
（1） X 的可能取值为1，2，3，P(X 1) ，P(X  2)  ，P(X 3)  ，
5 54 10 543 10
故抽取次数X的概率分布为：
X 1 2 3
3 3 1
P
5 10 10
3 3 1 3
E(X)1 2 3  .
5 10 10 2
3  3 3
（2）每次检验取到新球的概率均为 ，故 X ~ B5, ，所以E(X)5 3.
5  5 5
高三1月诊断测试 数学参考答案 第 1 页 共 4 页
{#{QQABSQQQgggIAAJAAAgCAw1YCAGQkAAAAKoOhAAAIAAAiAFABAA=}#}17. （15分）
（1）证明：因为 AC 2BC 2，所以BC 1，
 
因为2CAB  ，所以CAB  .
3 6
1 2
BC AC 
在ABC中，  ，即  sinB ，
sin A sinB sin
6
所以sinB 1，即 AB  BC.
又因为平面ABC  平面BCCB，平面 ABC 平面BCCB  BC，AB  平面ABC，
1 1 1 1
所以 AB 平面BCCB.
1 1
又BC 平面BCCB，所以AB  BC ，
1 1 1 1

在BBC 中，BB2，BC 1，CBB  ，
1 1 1 3

所以BC2 BB2 BC2 2BBBCcos 3，即BC  3，
1 1 1 3 1
所以BC  BC.
1
而AB  BC ， AB  平面ABC，BC 平面ABC， ABBC  B ，
1
所以BC 平面 ABC.
1
又BC 平面 ACB ，所以平面 ABC  平面 ACB.
1 1 1
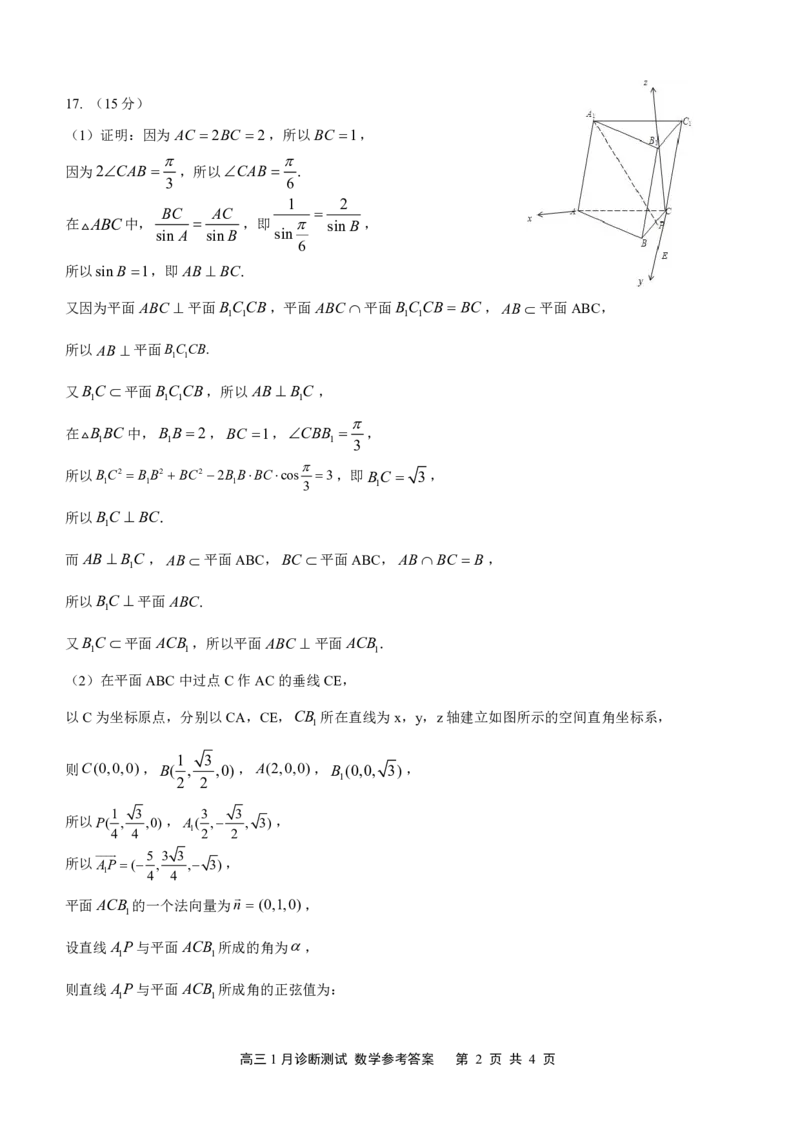
（2）在平面ABC中过点C作AC的垂线CE，
以C为坐标原点，分别以CA，CE，CB 所在直线为x，y，z轴建立如图所示的空间直角坐标系，
1
1 3
则C(0,0,0)，B( , ,0)，A(2,0,0)，B (0,0, 3)，
2 2 1
1 3 3 3
所以P( , ,0)，A( , , 3)，
4 4 1 2 2
 5 3 3
所以AP( , , 3)，
1 4 4

平面 ACB 的一个法向量为n  (0,1,0)，
1
设直线AP与平面 ACB 所成的角为，
1 1
则直线AP与平面 ACB 所成角的正弦值为：
1 1
高三1月诊断测试 数学参考答案 第 2 页 共 4 页
{#{QQABSQQQgggIAAJAAAgCAw1YCAGQkAAAAKoOhAAAIAAAiAFABAA=}#}3 3
 
  |APn| 4 3 3
sin|cos AP，n| 1    .
1 |AP||n| 25 27 10
1  3
16 16
18. （17分）
1
（1）解：设直线AB的方程为 y 2xt ，与 y2  4x联立得 y2 2y2t 0，  48t 0，得t  ，
2
设 A(x ,y )，B(x ,y )，C(x ,y )，则 y  y 2， y y 2t，
1 1 2 2 3 3 1 2 1 2
1
所以x x  (y  y 2t)1t，
1 2 2 1 2
      
由题意知F(1,0)，因为FA FB FC 0，FA(x 1,y )，FB (x 1,y )，FC (x 1,y )，
1 1 2 2 3 3
所以(x x x 3,y  y  y )(0,0)，
1 2 3 1 2 3
所以x x x 3,y  y  y 0, ，
1 2 3 1 2 3
所以x 2t,y 2,，即点C的坐标为(2t,2)， 代入抛物线E的方程得：44(2t)，解得t 1，满
3 3
1
足条件t  ，
2
所以直线AB的方程为2x y10.
（2）证明：设直线BC的方程为xmyn，与 y2  4x联立得 y2 4my4n 0，
16(m2 n)0，所以nm2， y  y 4m， y y 4n，
2 3 2 3
所以x x m(y  y )2n4m2 2n.
2 3 2 3
由(1)知x x x 3,y  y  y 0,，所以  x 34m2 2n,y 4m.，
1 2 3 1 2 3 1 1
即点A的坐标为(34m2 2n,4m).
3
又点A在抛物线 y2  4x上，所以16m2 4(34m2 2n)，所以n 4m2，
2
1
又nm2，所以m2  ，所以点A的横坐标34m2 2n4m2 2 ，
2
同理可证，B，C两点的横坐标也小于2.
所以ABC三个顶点的横坐标均小于2.
19. （17分）
    
（1）解：对于①，设kk 0，则可得k 2k 0，所以,线性相关；
1 2 1 2
高三1月诊断测试 数学参考答案 第 3 页 共 4 页
{#{QQABSQQQgggIAAJAAAgCAw1YCAGQkAAAAKoOhAAAIAAAiAFABAA=}#}对于②，设k  k   k  0  ，则可得k 2k 5k 0k 2k k 0k 2k 4k 0，所以k 2k 0，
1 2 3 1 2 3 1 2 3 1 2 3 1 2
  
k 0，所以,,线性相关；
3
对 于 ③ ， 设 k  k   k  k  0  ， 则 可 得 k k k 0k k k 0k k k 0 ， 解 得
1 2 3 4 1 2 4 1 3 4 2 3 4
1    
k k k  k ，所以,,,线性相关；
1 2 3 2 4
      
（2）解：设k ()k ()k ()0，
1 2 3
   
则(k k )(k k )(k k )0，
1 3 1 2 2 3
因为向量  ，  ，  线性无关，所以k k 0k k 0k k 0，解得k k k 0，
1 3 1 2 2 3 1 2 3
     
所以向量，，线性无关，
   
（3）①k k  k  0，如果某个k 0，i 1，2，⋯ ，m，
1 1 2 2 m m i
     
则k k  k  k  k   0，
1 1 2 2 i1 i1 i1 i1 m m
因为任意m1个都线性无关，所以k ，k ，⋯ k ，k ，⋅ ⋅ ⋅ ，k 都等于0，
1 2 i1 i1 m
所以这些系数k ，k ，⋅ ⋅ ⋅ ，k 或者全为零，或者全不为零，
1 2 m
②因为l 0，所以l ，l ，⋅ ⋅ ⋅ ，l 全不为零，
1 1 2 m
     l  l 
所以由l l l   0可得  2  m ，
1 1 2 2 m m 1 l 2 l m
1 1
    l  l    
代入k k  k   0可得k ( 2  m )k  k  0 ，
1 1 2 2 m m 1 l 2 l m 2 2 m m
1 1
l  l  
所以( 2 k k ) ( mk k ) 0 ，
l 1 2 2 l 1 m m
1 1
l l
所以 2 k k 0，⋯ ， m k k 0，
l 1 2 l 1 m
1 1
k k k
所以 1  2  m.
l l l
1 2 m
高三1月诊断测试 数学参考答案 第 4 页 共 4 页
{#{QQABSQQQgggIAAJAAAgCAw1YCAGQkAAAAKoOhAAAIAAAiAFABAA=}#}