文档内容
绝密★使用前
东北育才学校科学高中部 2023-2024 学年度高考适应性测试(一)
高 三 数 学
考生注意:
1.本试卷共150分,考试时间120分钟。分四大题,22小题,共6页
2.请将各题答案填写在答题卡上。
3.本试卷主要考试内容:高考全部内容
一、单选题(每题只有一个选项是正确答案,每题5分,共40分)
1.欧拉公式 (其中 , 为虚数单位)是由瑞士著名数学家欧拉创立,该公式建立了三
角函数与指数函数的关系,在复变函数论中占有非常重要的地位,被誉为“数学中的天桥”根据欧拉公式,下列
结论中正确的是( )
A. 的实部为 B. 在复平面内对应的点在第一象限
C. D. 的共轭复数为
2.在 中,角A,B,C对边分别为a,b,c.命题 ,命题 为等腰三角
形.则p是q的( )
A.充分不必要条件 B.必要不充分条件
C.充要条件 D.既不充分也不必要条件
3.“阿基米德多面体”也称为半正多面体,半正多面体是由两种或多种正多边形面组成,而又不属于正多面体的
凸多面体.如图,某广场的一张石凳就是一个阿基米德多面体,它是由正方体截去八个一样的四面体得到的.若
被截正方体的棱长为 ,则该阿基米德多面体的表面积为( )
A. B.
C. D.
4.公元 年,唐代李淳风注《九章》时提到祖暅的开立圆术.祖暅在求球体积时,使用一个原理:“幂势既同,
则积不容异”,意思是两个同高的立体,如在等高处的截面积恒相等,则体积相等.上述原理在中国被称为祖暅原
理,我们可以应用此原理将一些复杂几何体转化为常见几何体的组合体来计算体积.如图,将双曲线
与直线 所围成的平面图形绕双曲线的实轴所在直线旋转一周得到几何体 ,下列平面图形绕其对称轴(虚线
所示)旋转一周所得几何体与 的体积相同的是( )
高三数学 第 1 页
学科网(北京)股份有限公司A.图①,长为 、宽为 的矩形的两端去掉两个弦长为 、半径为 的弓形
B.图②,长为 、宽为 的矩形的两端补上两个弦长为 、半径为 的弓形
C.图③,长为 、宽为 的矩形的两端去掉两个底边长为 、腰长为 的等腰三角形
D.图④,长为 、宽为 的矩形的两端补上两个底边长为 、腰长为 的等腰三角形
5.已知正实数a,b满足 ,则 的最小值为( )
A. B.3 C. D.
6.英国物理学家牛顿用“作切线”的方法求函数的零点时,给出的“牛顿数列”在航空航天中应用广泛,若数列
满足 ,则称数列 为牛顿数列,如果 ,数列 为牛顿数列,设
且 , ,数列 的前 项和为 ,则 ( )
A. B. C. D.
7.在 中, , , , 为线段 上的动点,且 ,则
的最小值为( )
A. B. C. D.
8.设正实数 , , 分别满足 ,则 , , 的大小关系为( )
A. B. C. D.
二、多选题(每题至少有一个选项为正确答案,少选且正确得3分,每题5分,共20分)
9.“世界杂交水稻之父”袁隆平发明了“三系法”籼型杂交水稻,成功研究出“两系法”杂交水稻,创建了超级
高三数学 第 2 页
学科网(北京)股份有限公司杂交稻技术体系.某水稻种植研究所调查某地杂交水稻的株高,得出株高(单位:cm)服从正态分布,其分布密
度函数 , ,则( )
A.该地杂交水稻的平均株高为100cm
B.该地杂交水稻株高的方差为10
C.该地杂交水稻株高在120cm以上的数量和株高在80cm以下的数量一样多
D.随机测量该地的一株杂交水稻,其株高在 和在 的概率一样大
10.对于正弦函数 ,当 时, 关于 的函数称为“反正弦函数”,记作 ,
如: ;同样的,对于余弦函数 ,当 时, 关于 的函数称为“反余弦函数”,记
作 ,如 ,则下列说法正确的是( )
A.“反正弦函数”与“反余弦函数”的定义域均为
B.“反正弦函数”与“反余弦函数”的单调性相同
C.“反正弦函数”是奇函数,“反余弦函数”是偶函数
D.若 , ,且 ,则
11.在 中,P,Q分别为边AC,BC上一点,BP,AQ交于点D,且满足 , ,
, ,则下列结论正确的为( )
A.若 且 时,则 ,
B.若 且 时,则 ,
C.若 时,则
D.
12.一般地,若函数 的定义域为 ,值域为 ,则称 为 的“ 倍跟随区间”;特别地,若
函数 的定义域为 ,值域也为 ,则称 为 的“跟随区间”.下列结论正确的是( )
A.若 为 的跟随区间,则
高三数学 第 3 页
学科网(北京)股份有限公司B.函数 不存在跟随区间
C.若函数 存在跟随区间,则
D.二次函数 存在“3倍跟随区间”
三、填空题(每题5分,共20分)
13.科拉茨是德国数学家,他在1937年提出了一个著名的猜想:任给一个正整数 ,如果 是偶数,就将它减半
(即 );如果 是奇数,则将它乘3加1(即 ),不断重复这样的运算,经过有限步后,一定可以得到1.
这是一个很有趣的猜想,但目前还没有证明或否定.如果对正整数 (首项)按照上述规则施行变换后的第8项为1
(注:1可以多次出现),则满足条件的 的所有不同值的和为___________.
14.已知 ,则 _____________.
15.已知 ,过点 倾斜角为 的直线 交 于 、 两点( 在第一象限内),过点 作
轴,垂足为 ,现将 所在平面以 轴为翻折轴向纸面外翻折,使得 ,则几何体 外接球
的表面积为______.
16.“一尺之棰,日取其半,万世不竭”出自我国古代典籍《庄子·天下》,其中蕴含着等比数列的相关知识.已知
长度为4的线段 ,取 的中点 ,以 为边作等边三角形(如图①),该等边三角形的面积为 ,在图①
中取 的中点 ,以 为边作等边三角形(如图②),图②中所有的等边三角形的面积之和为 ,以此类推,
则 ___________; ___________.
四、解答题(17题10分,其余每题12分,共70分)
17.如图,已知曲线 及曲线 .从 上的点 作直线平行于 轴,交曲线
于点 ,再从点 作直线平行于 轴,交曲线 于点 ,点 的横坐标构成数列 .
高三数学 第 4 页
学科网(北京)股份有限公司(1)试求 与 之间的关系,并证明: ;
(2)若 ,求 的通项公式.
18.已知 的内角 所对的边分别为 .
(1)求 ;
(2) 为 内一点, 的延长线交 于点 ,___________,求 的面积.
请在下列两个条件中选择一个作为已知条件补充在横线上,并解决问题.
① 的三个顶点都在以 为圆心的圆上,且 ;
② 的三条边都与以 为圆心的圆相切,且 .
注:如果选择多个条件分别解答,按第一个解答记分.
19.中国共产党第二十次全国代表大会上的报告中提到,新时代十年我国经济实力实现历史性跃升,国内生产总
值从54万亿元增长到114万亿元,我国经济总量稳居世界第二位.建立年份编号为解释变量,地区生产总值为响应
变量的一元线性回归模型,现就2012-2016某市的地区生产总值统计如下:
201
年份 2013 2014 2015 2016
2
年份编号 1 2 3 4 5
地区生产总值(亿元) 2.8 3.1 3.9 4.6 5.6
(1)求出回归方程,并计算2016年地区生产总值的残差;
(2)随着我国打赢了人类历史上规模最大的脱贫攻坚战,该市2017-2022的地区生产总值持续增长,现对这11年的
数据有三种经验回归模型 、 、 ,它们的 分别为0.976、
0.880和0.985,请根据 的数值选择最好的回归模型预测一下2023年该市的地区生产总值;
高三数学 第 5 页
学科网(北京)股份有限公司(3)若2012-2022该市的人口数(单位:百万)与年份编号的回归模型为 ,结合(2)问中的最佳模型,
预测一下在2023年以后,该市人均地区生产总值的变化趋势.
参考公式: , ;
20.蜂房是自然界最神奇的“建筑”之一,如图1所示.蜂房结构是由正六棱柱截去三个相等的三棱锥 ,
, ,再分别以 , , 为轴将 , , 分别向上翻转 ,使 , ,
三点重合为点 所围成的曲顶多面体(下底面开口),如图2所示.蜂房曲顶空间的弯曲度可用曲率来刻画,定义
其度量值等于蜂房顶端三个菱形的各个顶点的曲率之和,而每一顶点的曲率规定等于 减去蜂房多面体在该点的
各个面角之和(多面体的面角是多面体的面的内角,用弧度制表示).例如:正四面体在每个顶点有3个面角,每
个面角是 ,所以正四面体在各顶点的曲率为 .
(1)求蜂房曲顶空间的弯曲度;
(2)若正六棱柱底面边长为1,侧棱长为2,设
(i)用 表示蜂房(图2右侧多面体)的表面积 ;
(ii)当蜂房表面积最小时,求其顶点 的曲率的余弦值.
21.已知双曲线 : 的右焦点为 ,渐近线方程为 ,过 的直线与 的两条
渐近线分别交于 两点.
(1)求 的方程;
(2)若直线 的斜率为1,求线段 的中点坐标;
高三数学 第 6 页
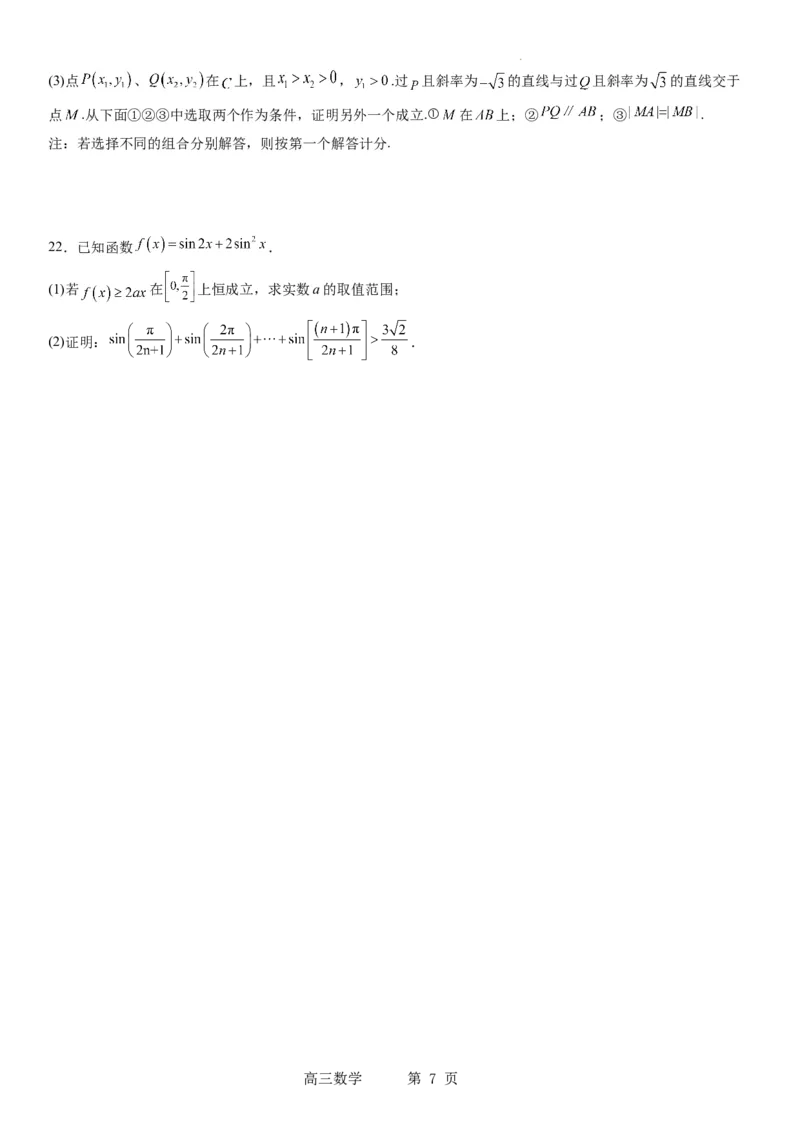
学科网(北京)股份有限公司(3)点 、 在 上,且 , .过 且斜率为 的直线与过 且斜率为 的直线交于
点 .从下面①②③中选取两个作为条件,证明另外一个成立.① 在 上;② ;③ .
注:若选择不同的组合分别解答,则按第一个解答计分.
22.已知函数 .
(1)若 在 上恒成立,求实数a的取值范围;
(2)证明: .
高三数学 第 7 页
学科网(北京)股份有限公司