文档内容
数学参考答案
一、单项选择题(本大题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只
有一项符合题目要求)
题号 1 2 3 4 5 6 7 8
答案 A B B A D C C D
【解析】
1.因为 ,所以 的虚部为2,故选A.
2. , ,所以 ,故选B.
3. 展开式的通项公式为 ,令 ,得 ,则 的
系数为 ,故选B.
4 . 设 等 比 数 列 的 公 比 为 , 由 题 知 , 所 以 . 又
,故选A.
5.易知焦点三角形 的面积为1,故 ,所以 ,则
,故选D.
6.据题意, 应是 的一个变号零点,由于 ,故 ,故选C.
7.所有对局中,恰有一组对局是不公平对局的情况为:2名外挂玩家都分到了同一组对局,
记该事件为事件 ,则 ,故选C.
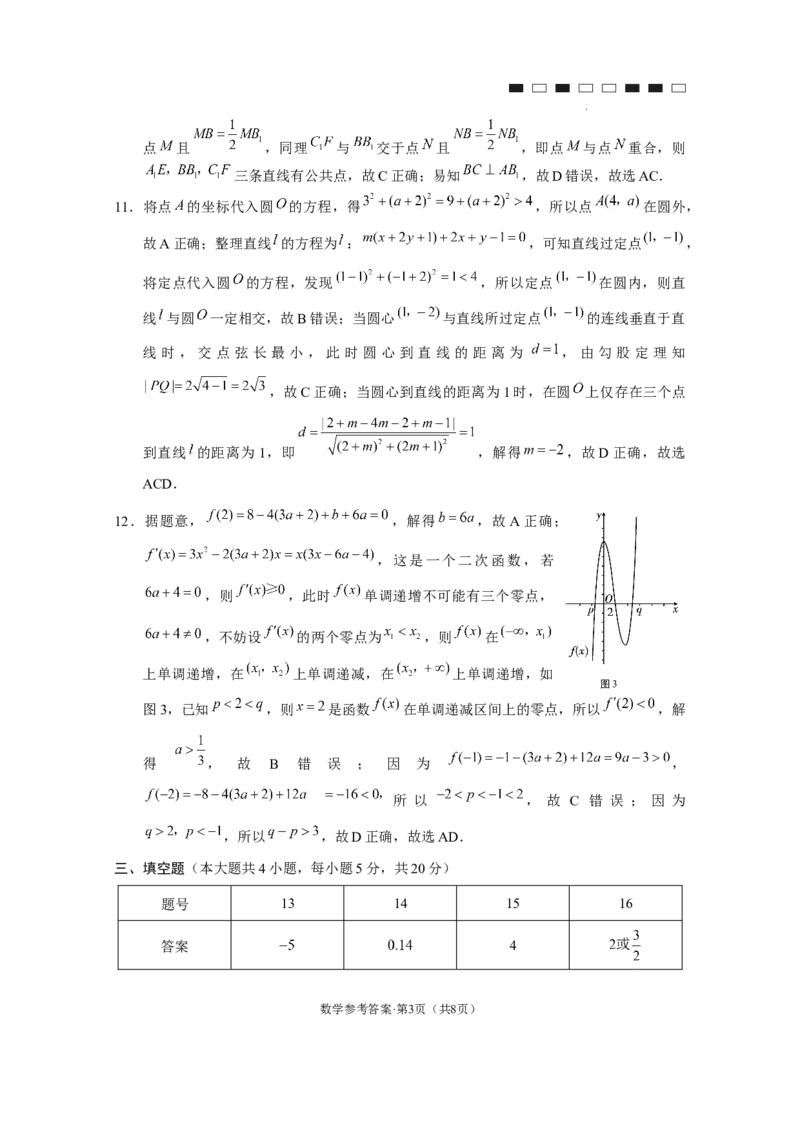
8.如图1,设 的外接圆圆心为 ,半径为 , 的外接
圆圆心为 ,半径为 ,记 所在平面为 , 所在平
面为 ,连接 ,则 .在 中,
,则 ,平面 与球面的交线为圆,
图1
数学参考答案·第1页(共8页)
学科网(北京)股份有限公司该圆就是 的外接圆,由正弦定理知 ;取 的中点为
,根据垂径定理知 ,则 平面 ,故 为二面
角的平面角,即 ;在 中, ,由勾股定理得
,易知 四点共面,在 中, ,
由 勾 股 定 理 得 , 如 图 在 四 边 形 中 ,
,知 四点共圆,记该圆为圆 ,则
为圆 的直径,在 中,由正弦定理得 ,解得 ,由余
弦 定 理 得 , 解 得 , 在
中, ,由勾股定理得 ,即圆 的半径
为 ,故交线长为 ,故选D.
二、多项选择题(本大题共4小题,每小题5分,共20分.在每小题给出的四个选项中,有
多项符合题目要求,全部选对的得5分,选对但不全的得2分,有选错的得0分)
题号 9 10 11 12
ABD
答案 AC ACD AD
【解析】
9.由题知, 的周期为 ,故 ,所以A正确; ,故 的
最大值为 ,所以B正确;当 时, ,显然 不单调,
故C错误;当 时, ,故 是 的一个对称中心,所以D正确,
故选ABD.
10. 平面 , 平面 , ,故
A正确;如图2,显然 与 是异面直线,故B错误;在
平面 中, ,且 ,则 与 交于
图2
数学参考答案·第2页(共8页)
学科网(北京)股份有限公司点 且 ,同理 与 交于点 且 ,即点 与点 重合,则
三条直线有公共点,故C正确;易知 ,故D错误,故选AC.
11.将点 的坐标代入圆 的方程,得 ,所以点 在圆外,
故A正确;整理直线 的方程为 : ,可知直线过定点 ,
将定点代入圆 的方程,发现 ,所以定点 在圆内,则直
线 与圆 一定相交,故B错误;当圆心 与直线所过定点 的连线垂直于直
线 时 , 交 点 弦 长 最 小 , 此 时 圆 心 到 直 线 的 距 离 为 , 由 勾 股 定 理 知
,故C正确;当圆心到直线的距离为1时,在圆 上仅存在三个点
到直线 的距离为1,即 ,解得 ,故D正确,故选
ACD.
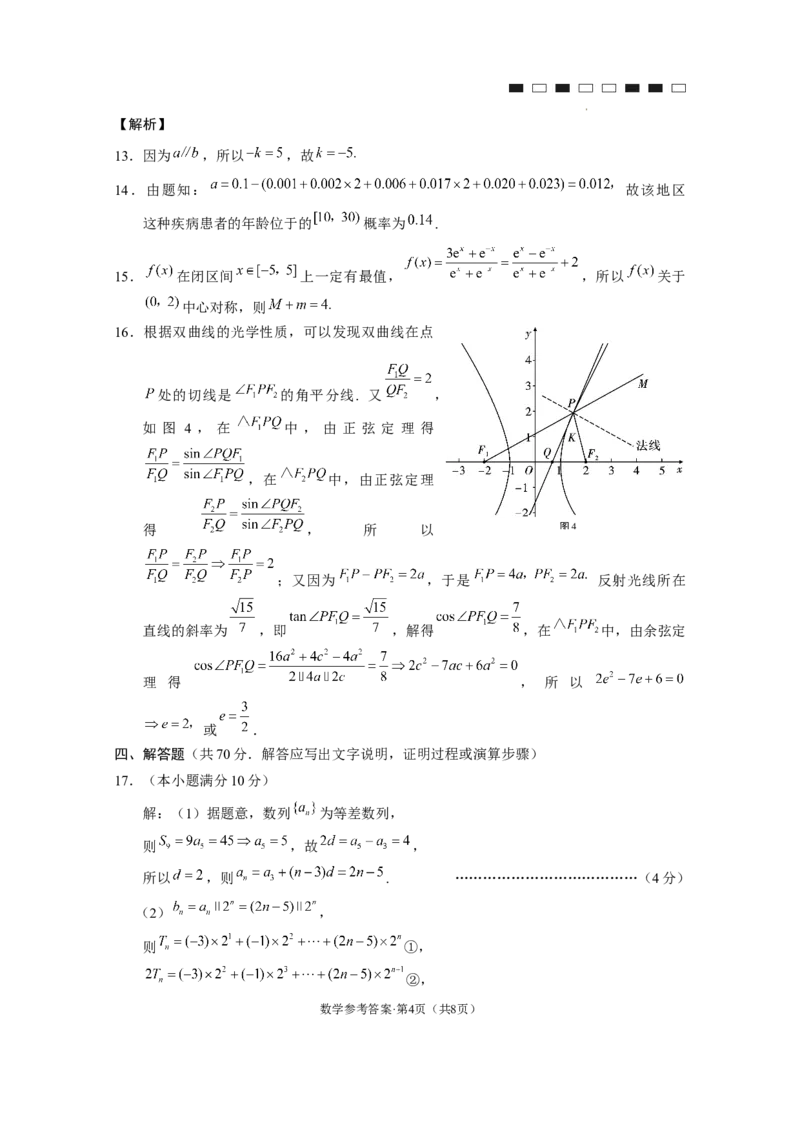
12.据题意, ,解得 ,故A正确;
,这是一个二次函数,若
,则 ,此时 单调递增不可能有三个零点,
,不妨设 的两个零点为 ,则 在
上单调递增,在 上单调递减,在 上单调递增,如
图3
图3,已知 ,则 是函数 在单调递减区间上的零点,所以 ,解
得 , 故 B 错 误 ; 因 为 ,
所 以 , 故 C 错 误 ; 因 为
,所以 ,故D正确,故选AD.
三、填空题(本大题共4小题,每小题5分,共20分)
题号 13 14 15 16
答案 4
数学参考答案·第3页(共8页)
学科网(北京)股份有限公司【解析】
13.因为 ,所以 ,故
14.由题知: 故该地区
这种疾病患者的年龄位于的 概率为 .
15. 在闭区间 上一定有最值, ,所以 关于
中心对称,则
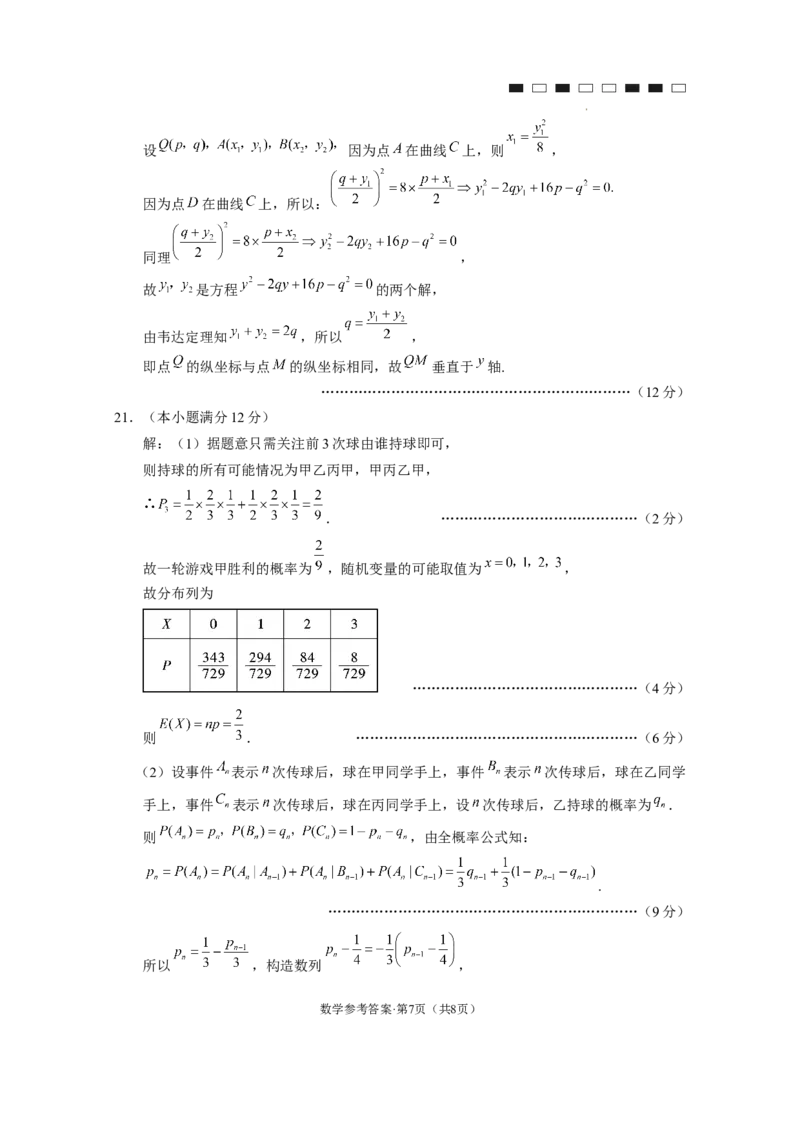
16.根据双曲线的光学性质,可以发现双曲线在点
处的切线是 的角平分线. 又 ,
如 图 4 , 在 中 , 由 正 弦 定 理 得
,在 中,由正弦定理
得 , 所 以 图4
;又因为 ,于是 反射光线所在
直线的斜率为 ,即 ,解得 ,在 中,由余弦定
理 得 , 所 以
或 .
四、解答题(共70分.解答应写出文字说明,证明过程或演算步骤)
17.(本小题满分10分)
解:(1)据题意,数列 为等差数列,
则 ,故 ,
所以 ,则 . …………………………………(4分)
(2) ,
则 ①,
②,
数学参考答案·第4页(共8页)
学科网(北京)股份有限公司由① ②得 ,
则 …………………………………(10分)
18.(本小题满分12分)
解:(1)因为 ,又 ,
所以 .
又 ,由勾股定理得 ,
又 ,
所以 ,故 .
因为 ,
所以 ,则 为点 到平面 的距离,
故点 到平面 的距离为2. ……………………………………………(5分)
(2)在平面 内过点 作 的平行线 ,则 ,以
为坐标原点,以 所在直线为 轴, 所在直线为 轴, 所在直线为 轴建立空
间直角坐标系.
由勾股定理得:
5,则
如图
,
图5
设平面 的法向量为 ,
则 即 取 ,则
设平面 的法向量为 ,
则 即 取 ,则
数学参考答案·第5页(共8页)
学科网(北京)股份有限公司所以
记二面角 的大小为 ,则 ,
故二面角的正弦值为 . ………………………………………………(12分)
19.(本小题满分12分)
解:(1)在 中,因为 ,
所以 ,
则 ,
解得 …………………………………………………………(6分)
(2)如图6,设 与 交于点 ,连接 并延长交 于
点 ,
由 于 , 知 , 且 点 满 足
,
则在 中,由余弦定理得
图6
,
又 ,
故 ,
所以 …………………………………………………………(12分)
20.(本小题满分12分)
(1)解:设点 ,据题意 ,解得
由于点 不在一条射线上,
故点 的轨迹方程为 : . ……………………………………………(5分)
(2)证明:设线段 的中点分别为 ,
数学参考答案·第6页(共8页)
学科网(北京)股份有限公司设 因为点 在曲线 上,则 ,
因为点 在曲线 上,所以:
同理 ,
故 是方程 的两个解,
由韦达定理知 ,所以 ,
即点 的纵坐标与点 的纵坐标相同,故 垂直于 轴.
…………………………………………………………(12分)
21.(本小题满分12分)
解:(1)据题意只需关注前3次球由谁持球即可,
则持球的所有可能情况为甲乙丙甲,甲丙乙甲,
. ……………………………………(2分)
故一轮游戏甲胜利的概率为 ,随机变量的可能取值为 ,
故分布列为
…………………………………………(4分)
则 . ……………………………………………………(6分)
(2)设事件 表示 次传球后,球在甲同学手上,事件 表示 次传球后,球在乙同学
手上,事件 表示 次传球后,球在丙同学手上,设 次传球后,乙持球的概率为 .
则 ,由全概率公式知:
.
…………………………………………………………(9分)
所以 ,构造数列 ,
数学参考答案·第7页(共8页)
学科网(北京)股份有限公司解得 …………………………………………………………(12分)
22.(本小题满分12分)
解:(1)设定义域为 , ,
当 时, , 在定义域上单调递增;
当 时, 在 上单调递增,在 上单调递减.
…………………………………………………………(5分)
(2)已知不等式等价为 ,
即 .
记 ,
的定义域为 , ,
观察知 ,
故 的表达式可以因式分解,
当 时,在 上, ,即 在 上单调递增, ,则
,解得 ,故 ;
当 时,在 上, ,即 在 上单调递减, ,
则 ,解得 ,此时 无解;
当 时 , 在 上 单 调 递 增 , 在 上 单 调 递 减 ,
,解得 ,此时 无解;
综上, 的取值范围为 …………………………………………………………(12分)
数学参考答案·第8页(共8页)
学科网(北京)股份有限公司数学参考答案·第9页(共8页)
学科网(北京)股份有限公司