(答案)如皋市2024届高三2月诊断测试数学参考答案_2024年3月_013月合集_2024届新高考19题（九省联考模式）数学合集140套_江苏南通市如皋市2024届高三下学期2月诊断测试数学试题+答案

如皋市 届高三 月诊断测试 2024 2 数学参考答案 2024.02 一、选择题：本题共8小题，每小题5分，共40分. 题号 1 2 3 4 5 6 7 8 答案 B C D D C C C B 二、选择题：本题共3小题，每小题6分，共18分.全部选对得6分，部分选对得3分，有选错得0分. 题号 9 10 11 答案 BC AD ACD 三、填空题：本题共3小题，每小题5分，共15分. 题号 12 13 14 答案 18 10 3 2 3 3 3 2 ( , )( , ) 2 2 2 2 四、解答题：本题共5小题，共77分.解答时应写出文字说明、证明过程或演算步骤. 15. （13分） 1 2x2 x1 (2x1)(x1) （1）函数的定义域为(0,)，当a 1时， f(x)2x1   ， x x x 当x(0,1), f(x) 0，函数单调递减；当x(1,), f(x)  0，函数单调递增， x1是函数的极小值点，函数的极小值为 f(1)1100 （2）若函数 y  f(x) 在(0,1)内单调递增， 1 1 1 1 则 f(x)2ax1 0在(0,1)恒成立，即a   在(0,1)恒成立. x 2x2 x 1 1 1 11 1 2 1 因为        (1,)，所以使得函数 y  f(x) 在(0,1)内单调递增的a不存在， 2x2 x 2x 2 4 1 若函数 y  f(x) 在(0,1)内单调递减，则 f(x)2ax1 „0在(0,1)恒成立， x 1 1 1 1 1 1 11 1 2 1 即a„   在(0,1)恒成立.即a„        在(0,1)恒成立. 2x2 x 2x2 x 2x 2 4 1 1 1 11 1 2 1 又因为        (1,)， 2x2 x 2x 2 4 所以a„1时，函数 y  f(x) 在(0,1)内单调递减. 综上，当a„1时，使得函数 y  f(x) 在(0,1)内单调递减. 高三2月诊断测试 数学参考答案 第 1 页 共 4 页 {#{QQABDYqAogAIAAJAAAhCAwXYCkAQkAAAAAoGREAIIAAByBFABAA=}#}16. 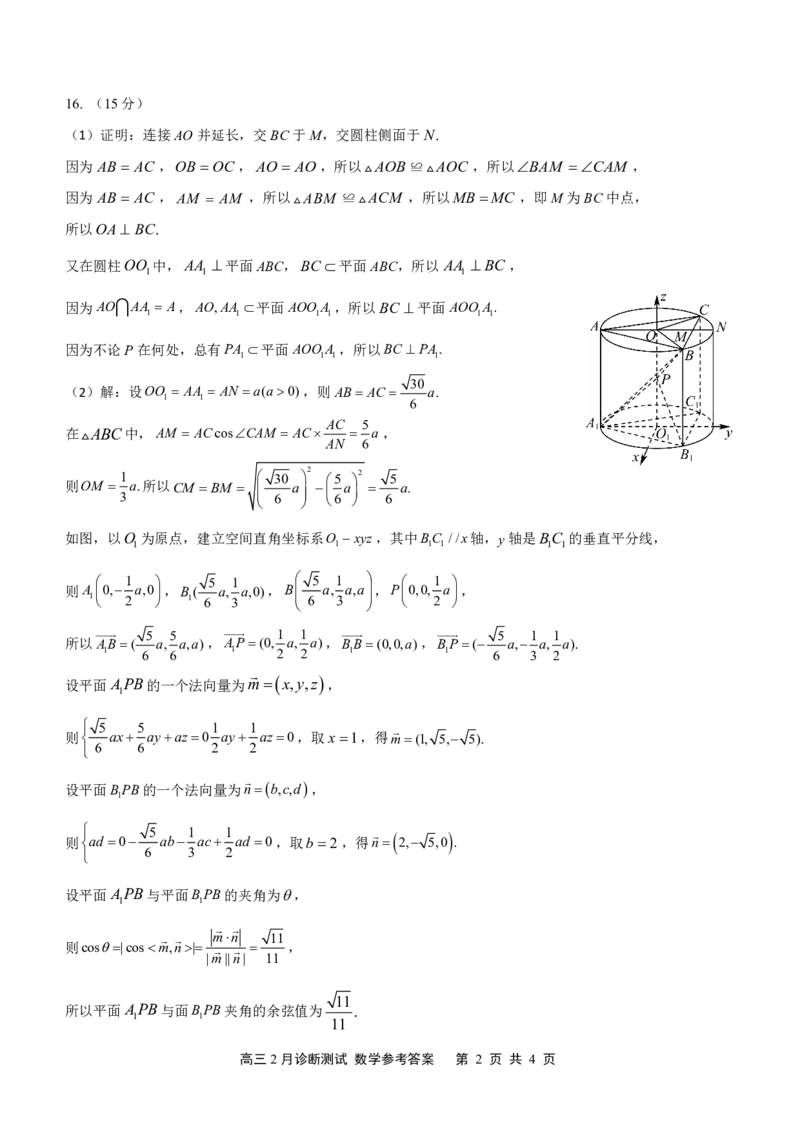（15分） （1）证明：连接AO并延长，交BC于M，交圆柱侧面于N. 因为 AB  AC ，OB OC ，AO AO ，所以AOB≌AOC ，所以BAM CAM ， 因为 AB  AC ，AM  AM ，所以ABM ≌ACM ，所以MB MC ，即M为BC中点， 所以OA BC. 又在圆柱OO 中， AA 平面ABC，BC 平面ABC，所以 AA  BC ， 1 1 1 因为AOAA  A，AO,AA 平面AOOA ，所以BC 平面AOO A. 1 1 1 1 1 1 因为不论P在何处，总有PA 平面AOOA ，所以BC PA. 1 1 1 1 30 （2）解：设OO  AA  AN a(a0)，则AB AC  a. 1 1 6 AC 5 在ABC中，AM  ACcosCAM  AC  a， AN 6 1  30  2 5  2 5 则OM  3 a.所以CM BM     6 a    6 a   6 a. 如图，以O 为原点，建立空间直角坐标系O xyz，其中BC //x轴，y轴是BC 的垂直平分线， 1 1 1 1 1 1  1  5 1  5 1   1  则A 1   0, 2 a,0  ，B 1 ( 6 a, 3 a,0)，B   6 a, 3 a,a   ，P  0,0, 2 a  ，  5 5  1 1   5 1 1 所以AB( a, a,a)，AP(0, a, a)，BB(0,0,a)，BP( a, a, a). 1 6 6 1 2 2 1 1 6 3 2  设平面APB的一个法向量为m x,y,z  ， 1  5 5 1 1  则 ax ayaz0 ay az0，取x 1，得m(1, 5, 5).  6 6 2 2  设平面BPB的一个法向量为nb,c,d， 1  5 1 1    则ad 0 ab ac ad 0，取b2，得n 2, 5,0 .  6 3 2 设平面APB与平面BPB的夹角为， 1 1     mn 11 则cos|cosm,n|    ， |m||n| 11 11 所以平面APB与面BPB夹角的余弦值为 . 1 1 11 高三2月诊断测试 数学参考答案 第 2 页 共 4 页 {#{QQABDYqAogAIAAJAAAhCAwXYCkAQkAAAAAoGREAIIAAByBFABAA=}#}17. （15分） （1）易知对于每次划拳比赛基本事件共有 339 个， 其中小华赢(或输)包含三种可能情况，他们平局也有三种可能情况， 不妨设事件“第 i(iN) 次划拳小华赢”为A；事件“第i次划拳小华平”为B ；事件“第i次划拳小华输”为C ， i i i 3 1 所以P(A)P(B)P(C )  . i i i 9 3 因为游戏结束时小华在第2个台阶，所以这包含两种可能的情况： 第一种：小华在第1个台阶，并且小明在第2个台阶，最后一次划拳小华平； 7 其概率为 p  A2P(B)P(C )P(B )P(C )P(A )P(C )P(B ) ， 1 2 1 2 3 1 2 3 4 81 第二种：小华在第2个台阶，并且小明也在第2个台阶，最后一次划拳小华输， 29 其概率为 p P(B)P(B )P(C )A3P(A)P(B )P(C )P(C ) A2P(A)P(C )P(A )P(C )P(C ) ， 2 1 2 3 3 1 2 3 4 2 1 2 3 4 5 243 7 29 50 所以游戏结束时小华在第2个台阶的概率为 p p  p    . 1 2 81 243 243 （2）依题可知X的可能取值为2、3、4、5， 1 2 P(X 5)2P(A)P(C )P(A )P(C )2( )4  ， 1 2 3 4 3 81 1 2 P(X 2)2P(A)P(A )2( )2  ， 1 2 3 9 P(X 3)2P(A)P(B )P(A )2P(B)P(A )P(A )P(B)P(B )P(B ) 1 2 3 1 2 3 1 2 3 13 2P(A)P(B )P(B )2P(B)P(A )P(B )2P(B)P(B )P(A ) 2P(C )P(A )P(A ) 1 2 3 1 2 3 1 2 3 1 2 3 27 22 P(X 4)1P(X 5)P(X 2)P(X 3) ， 81 所以X的分布列为： X 2 3 4 5 2 13 22 2 P 9 27 81 81 2 13 22 2 251 所以X的数学期望为：E(X)2 3 4 5  . 9 27 81 81 81 18. （17分） （1）由已知，设椭圆C 方程为 y2  x2 1，  t 0  ， 2 2t t y2 x2 且经过点(1, 2)，则t 2，故椭圆C 的标准方程为  1; 2 4 2 （2）根据题意，直线AP、AQ的斜率存在且不为0，A(0,2)， 高三2月诊断测试 数学参考答案 第 3 页 共 4 页 {#{QQABDYqAogAIAAJAAAhCAwXYCkAQkAAAAAoGREAIIAAByBFABAA=}#}设直线AP的斜率为k ，直线AQ的斜率为k ，设P(x ,y )，则Q(x ,y )， 1 2 0 0 0 0 y2 x2 y 2 y 2 y24 因为 0  0 1，所以y2 42x2，所以kk  0  0  0 2，即k k 2， 4 2 0 0 1 2 x x x2 1 2 0 0 0 直线AP:yk x2与x2 2y2 8，联立得(12k2)x2 8k x 0， 1 1 1 8k 8k 解得x  1 ，同理可得x  2 ， M 12k2 N 12k2 1 2 直线AP:yk x2与2x2  y2  4，联立得(2k2)x2 4k x0， 1 1 1 4k 4k 解得x  1 ，同理可得x  2 ， P 2k2 Q 2k2 1 2 S |AM ||AN| x x |64kk | (2k2)(2k2) 4(42k2 2k2 4) 328(k2 k2) 1   M  N  1 2  1 2  1 2  1 2 S |AP||AQ| x x (12k2)(12k2) |16kk | 2k2 2k2 17 172(k2 k2) 2 P Q 1 2 1 2 1 2 1 2 36 4 4 ，因为k2 k2 k2  4， 172(k2 k2) 1 2 1 k2 1 2 1 4 S 64 当且仅当k2  ，即k  2时，等号成立，故 1 的取值范围为[ ,4). 1 k2 1 S 25 1 2 19. （17分） 1 3 3 1 2 13 13 （1）①S  1  ,S     ，所以，S S ； 1 2 2 4 2 6 3 6 54 1 2 1 5 ②{ ,1, };(答案不唯一) 3 3 （2）S S； 证明：不妨设i1, j2，则a 1a ； 1 2 则aa a 1,a 1,a a ,a a ； 1 1 2 2 3 3 4 4 所以SSaa a a aa a a aa a a 1a a a 1a 1a a 0； 1 2 3 4 1 2 3 4 1 2 1 2 3 4 1 2 3 4 所以S S； （3） S的最大值为1，当且仅当a a a 1时，取到最大值. 1 2 n 证明：因为a 0(i1,2,,n)，且a a a n； i 1 2 n a a a  n 所以，S a a a „ 1 2 n  1； 1 2 n  n  当且仅当a a a 1时，等号成立. 1 2 n 高三2月诊断测试 数学参考答案 第 4 页 共 4 页 {#{QQABDYqAogAIAAJAAAhCAwXYCkAQkAAAAAoGREAIIAAByBFABAA=}#}