文档内容
开远市第一中学校 2023 年秋季学期高三年级开学考试
数学
考生注意:
1.本试满分150分,考试时间120分钟.
2.回答选择题时,选出每小题答案后,用2B铅笔把答题卡上对应题目的答案标号涂黑.如需改
动,用橡皮擦干净后,再选涂其他答案标号.回答非选择题时,将答案写在答题卡上,写在本
试卷上无效.超出答题区域书写的答案无效,在试卷、草稿纸上作答无效.
一、选择题:本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是
符合题目要求的.
1. 已知i为虚数单位,若复数 ( )为纯虚数,则复数 在复平面上对应的点( )
A. 第一象限 B. 第二象限 C. 第三象限 D. 第四象限
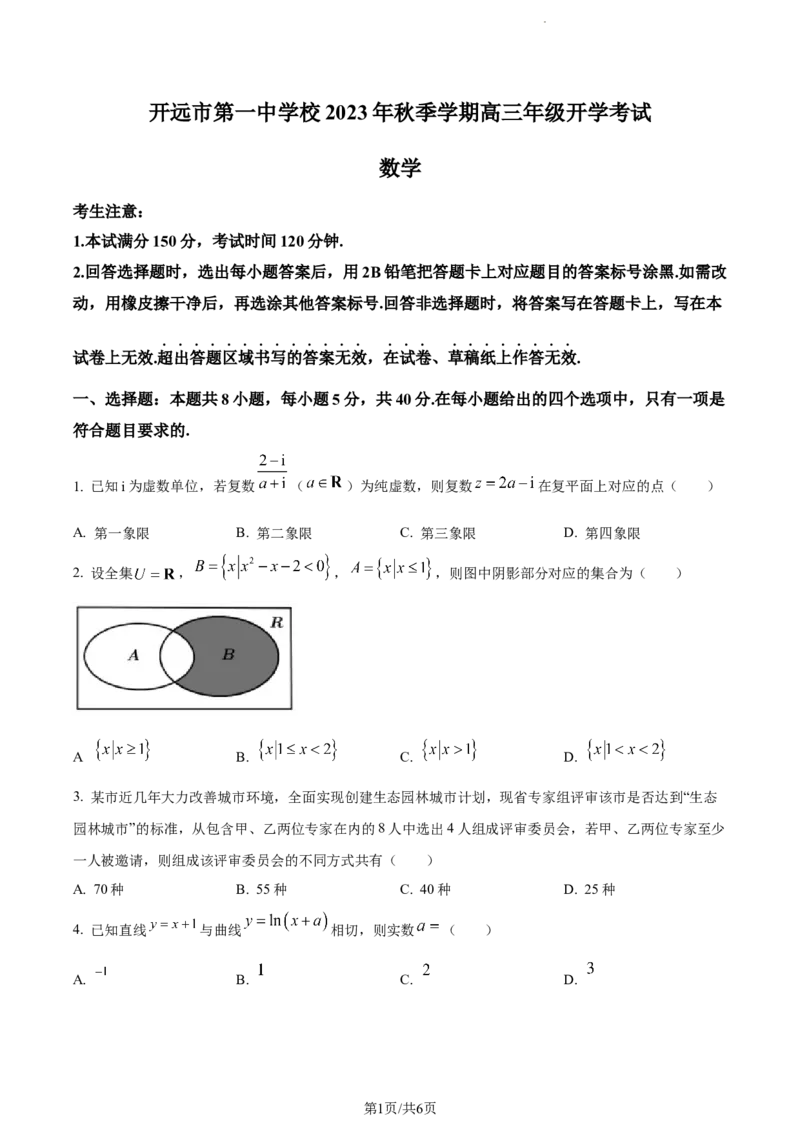
2. 设全集 , , ,则图中阴影部分对应的集合为( )
.
A B. C. D.
3. 某市近几年大力改善城市环境,全面实现创建生态园林城市计划,现省专家组评审该市是否达到“生态
园林城市”的标准,从包含甲、乙两位专家在内的8人中选出4人组成评审委员会,若甲、乙两位专家至少
一人被邀请,则组成该评审委员会的不同方式共有( )
A. 70种 B. 55种 C. 40种 D. 25种
4. 已知直线 与曲线 相切,则实数 ( )
A. B. C. D.
第1页/共6页
学科网(北京)股份有限公司5. 已知抛物线 : 的焦点为 ,抛物线 上有一动点 , ,则 的最小
值为( )
.
A 5 B. 6 C. 7 D. 8
6. 若函数 在区间( , )内存在最小值,则实数 的取值范围是( )
A. [-5,1) B. (-5,1)
C. [-2,1) D. (-2,1)
7. 在等差数列 中, ,其前n项和 为,若 ,则 ( )
A. B. C. D.
8. 在平面直角坐标系中,已知点 为角 终边上一点,若 , ,则
( )
A. B.
C. D.
二、多选题:本题共4小题,每小题5分,共20分.在每小题给出的选项中,有多项符合题目
要求.全部选对的得5分,部分选对的得2分,有选错的得0分.
9. 下列说法正确的有( )
A. 若一组样本数据 线性相关,则用最小二乘法得到的经验回归直线必经过样本中
心点
的
B. 根据分类变量 与 成对样本数据,计算得到 ,依据 的独立性检验
,则推断 与 无关不成立,即认为 与 有关联,此推断犯错误的概率不大于0.05
第2页/共6页
学科网(北京)股份有限公司C. 若随机变量 和 满足 ,则 ,
D. 若随机变量 ,且 ,则
10. 已知三棱锥 的各顶点都在球O上,点M,N分别是AC,CD的中点, 平面BCD,
, ,则下列说法正确的是( )
A. 三棱锥 的四个面均为直角三角形
B. 球O的表面积为
C. 直线BD与平面ABC所成角的正切值是
D. 点O到平面BMN的距离是
11. 已知圆 ,点 为圆 上一动点, 为坐标原点,则下列说法中正确的是(
)
的
A. 最大值为
B. 的最小值为
C. 直线 的斜率范围为
D. 以线段 为直径的圆与圆 的公共弦方程为
12. 若 ,则下列不等式对一切满足条件的 恒成立的是( )
A. B. C. D.
三、填空题:本题共4小题,每小题5分,共20分.
第3页/共6页
学科网(北京)股份有限公司13. 已知向量 与 的夹角为 ,且 ,则 在 方向上的投影向量的坐标为
__________.
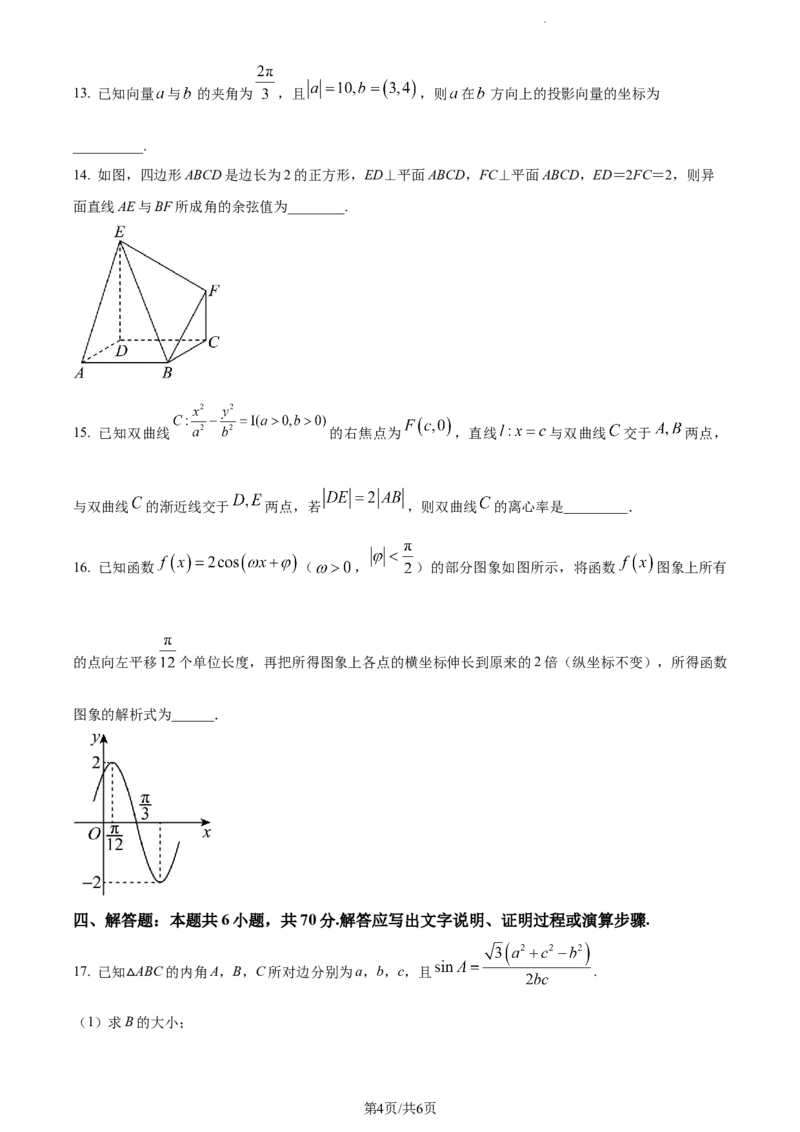
14. 如图,四边形ABCD是边长为2的正方形,ED⊥平面ABCD,FC⊥平面ABCD,ED=2FC=2,则异
面直线AE与BF所成角的余弦值为________.
15. 已知双曲线 的右焦点为 ,直线 与双曲线 交于 两点,
与双曲线 的渐近线交于 两点,若 ,则双曲线 的离心率是_________.
16. 已知函数 ( , )的部分图象如图所示,将函数 图象上所有
的点向左平移 个单位长度,再把所得图象上各点的横坐标伸长到原来的2倍(纵坐标不变),所得函数
图象的解析式为______.
四、解答题:本题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤.
17. 已知 ABC的内角A,B,C所对边分别为a,b,c,且 .
△
(1)求B的大小;
第4页/共6页
学科网(北京)股份有限公司(2)若 ABC为钝角三角形,且 ,求 ABC的周长的取值范围.
△ △
18. 已知 为数列 的前n项和, .
(1)证明:数列 为等比数列;
(2)设数列 的前n项和为 ,证明: .
19. 新能源汽车是指除汽油、柴油发动机之外的所有其他能源汽车,被认为能减少空气污染和缓解能源短
缺的压力.在当今提倡全球环保的前提下,新能源汽车越来越受到消费者的青睐,新能源汽车产业也必将成
为未来汽车产业发展的导向与目标.某机构从某地区抽取了500名近期购买新能源汽车的车主,调查他们的
年龄情况,其中购买甲车型的有200人.
(1)估计购买新能源汽车的车主年龄的平均数和中位数.
(2)将年龄不低于45岁的人称为中年,低于45岁的人称为青年,购买其他车型的车主青年人数与中年人
数之比为 .完成下列 列联表,依据 的独立性检验,能否认为购买甲车型新能源汽车与年
龄有关?
青年 中年 合计
甲车型
其他车型
合计
(3)用分层抽样的方法从购买甲车型的样本中抽取8人,再从中随机抽取4人,记青年有 人,求 的
分布列和数学期望.
第5页/共6页
学科网(北京)股份有限公司附: .
2.706 3.841 6.635 7.879
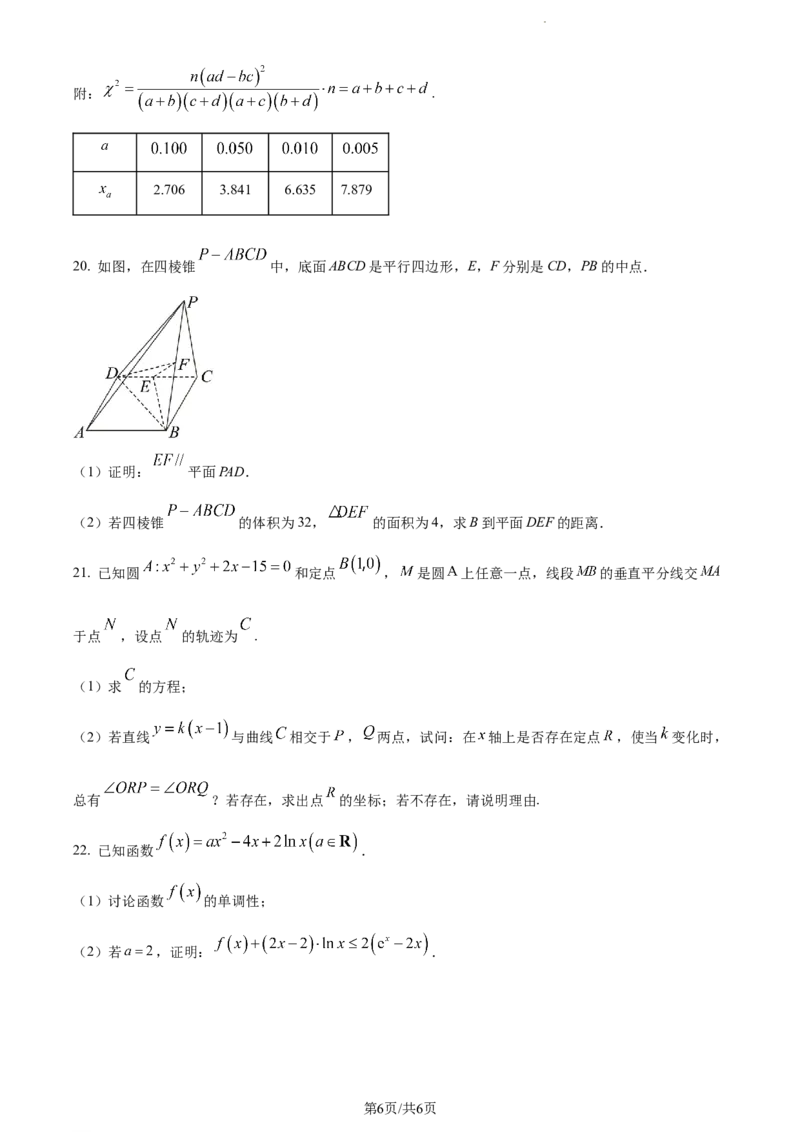
20. 如图,在四棱锥 中,底面ABCD是平行四边形,E,F分别是CD,PB的中点.
(1)证明: 平面PAD.
(2)若四棱锥 的体积为32, 的面积为4,求B到平面DEF的距离.
21. 已知圆 和定点 , 是圆 上任意一点,线段 的垂直平分线交
于点 ,设点 的轨迹为 .
(1)求 的方程;
(2)若直线 与曲线 相交于 , 两点,试问:在 轴上是否存在定点 ,使当 变化时,
总有 ?若存在,求出点 的坐标;若不存在,请说明理由.
22. 已知函数 .
(1)讨论函数 的单调性;
(2)若 ,证明: .
第6页/共6页
学科网(北京)股份有限公司