文档内容
2023-2024 学年度(上)阶段性考试(一)
高 2021 级数学(理科)
一、选择题(每个小题都有4个选项,其中只有1个正确选项,请把正确选项直接填涂在答
题卡相应位置上.每小题5分,共60分.)
1. 某同学计划2023年高考结束后,在A,B,C,D,E五所大学中随机选两所去参观,则 大学恰好被选
中的概率为( )
A. B. C. D.
2. 设集合 ,集合 , ,则 ( )
A. B.
C. D.
3. 已知复数 (x, )对应的点在第一象限,z的实部和虚部分别是双曲线C的实轴长和虚
轴长,若 ,则双曲线C的焦距为( )
A. 8 B. 4 C. D. 2
4. 展开式中 的系数为( )
A. B. C. D.
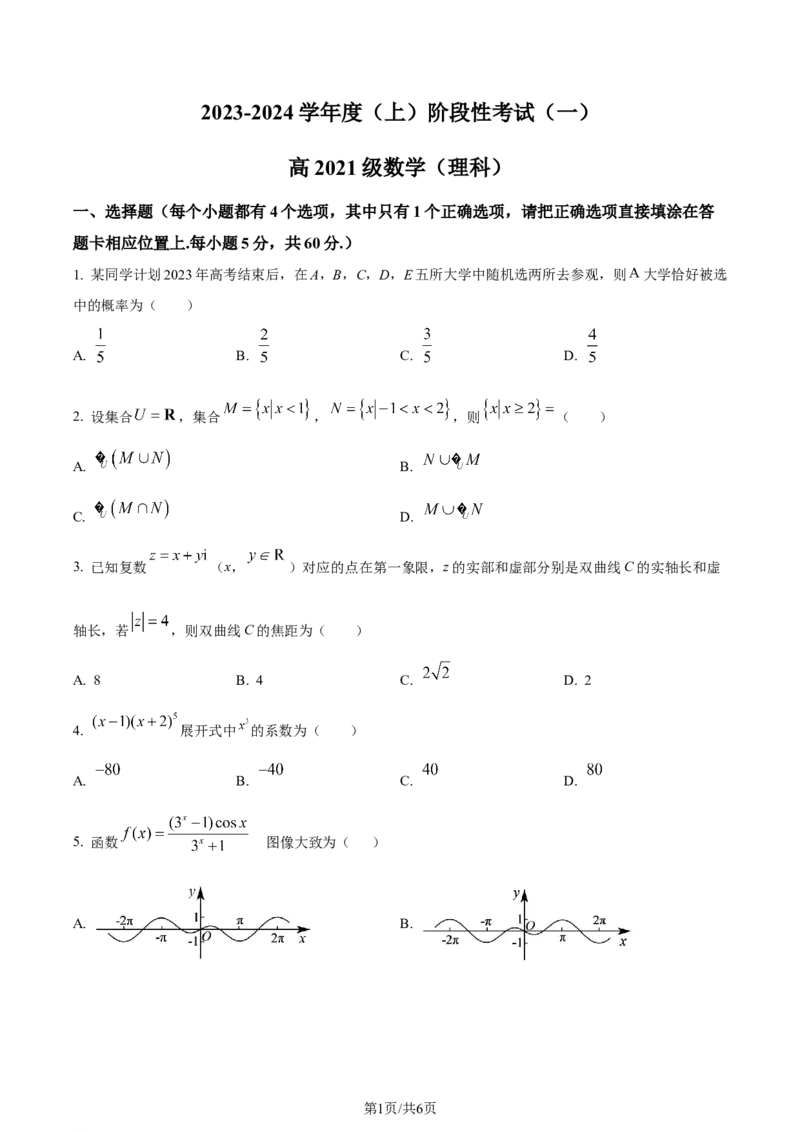
5. 函数 的图像大致为( )
A. B.
第1页/共6页
学科网(北京)股份有限公司C. D.
6. 将六位数“ ”重新排列后得到不同的六位偶数的个数为 ( )
A. B. C. 216 D.
7. 设 ,则 ( )
A. B. C. D.
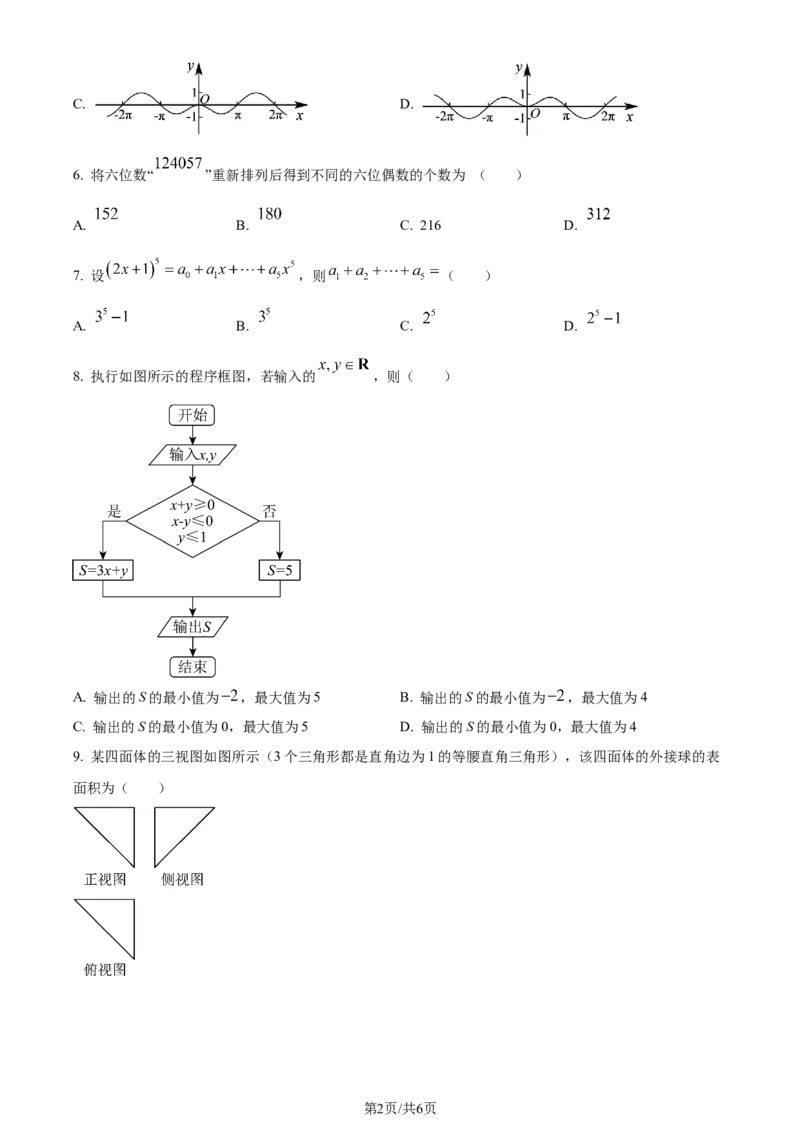
8. 执行如图所示的程序框图,若输入的 ,则( )
A. 输出的S的最小值为 ,最大值为5 B. 输出的S的最小值为 ,最大值为4
C. 输出的S的最小值为0,最大值为5 D. 输出的S的最小值为0,最大值为4
9. 某四面体的三视图如图所示(3个三角形都是直角边为1的等腰直角三角形),该四面体的外接球的表
面积为( )
第2页/共6页
学科网(北京)股份有限公司.
A B. C. D.
10. 2021年是巩固脱贫攻坚成果的重要一年,某县为响应国家政策,选派了6名工作人员到A 、B、C三
个村调研脱贫后的产业规划,每个村至少去1人,不同的安排方式共有( )种.
A. 540 B. 480 C. 360 D. 240
11. 设 是定义在 上的偶函数,且当 时, ,若对任意的 ,不等式
恒成立,则正数 的取值范围为( )
A. B. C. D.
12. 如图,一个棱长1分米的正方体形封闭容器中盛有V升的水,若将该容器任意放置均不能使水平面呈
三角形,则V的取值范围是( )
A. B. C. D.
二、填空题(请把每个小题的答案直接填写在答题卡相应位置上,每小题5分,共20分.)
13. 已知随机变量 ,若 ,则 ___________.
.
14 已知向量 , .若向量 与 垂直,则 ________.
15. 已知双曲线 的左、右焦点分别为 ,过 作一条直线与双曲线右支交于
两点,坐标原点为 ,若 ,则该双曲线的离心率为___________.
16. 若函数 在 上单减,则实数 的取值范围为______.
三、解答题(解答须写出必要的文字说明,推理过程和演算步骤)
第3页/共6页
学科网(北京)股份有限公司17. 为了有针对性地提高学生体育锻炼的积极性,某校需要了解学生是否经常锻炼与性别因素有关,为此
随机对该校100名学生进行问卷调查,得到如下列联表.
经常锻
不经常锻炼 总计
炼
男 35
女 25
总计 100
已知从这100名学生中任选1人,经常锻炼的学生被选中的概率为 .
附: .
0.1 0.05 0.01 0.001
.
2.706 3.841 6635 10.828
(1)完成上面的列联表;
(2)根据列联表中的数据,判断能否有90%的把握认为该校学生是否经常锻炼与性别因素有关.
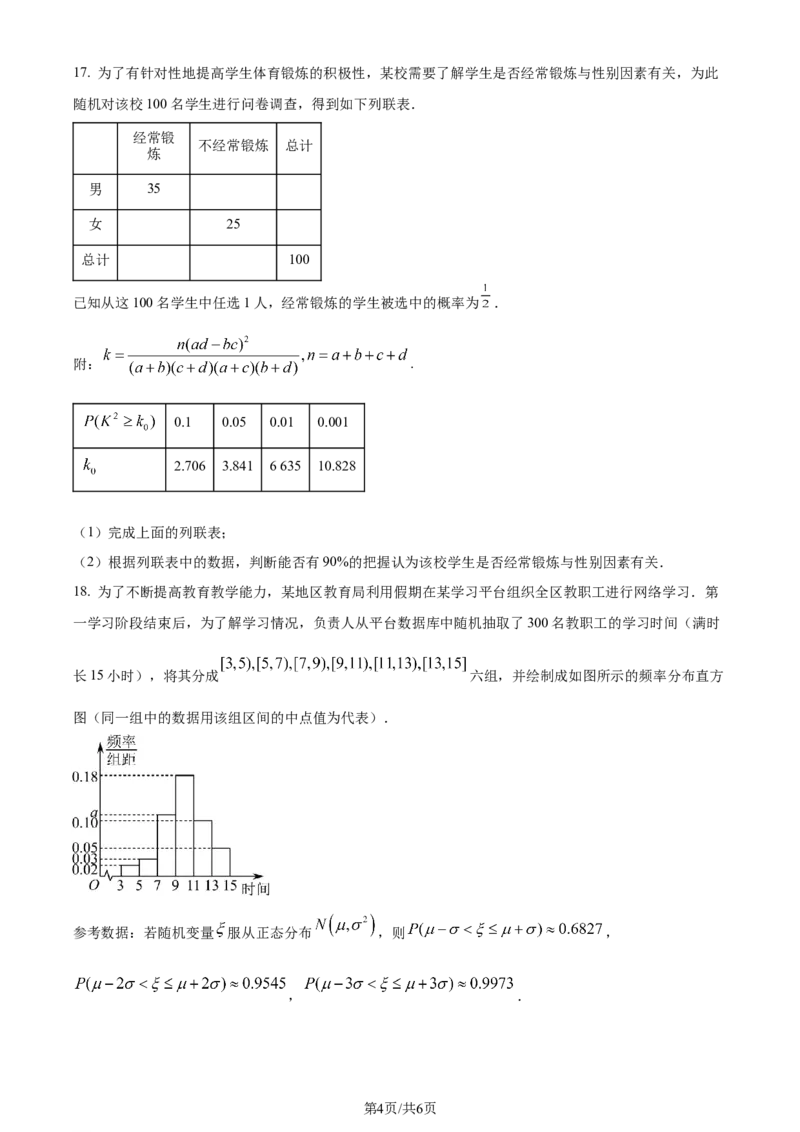
18. 为了不断提高教育教学能力,某地区教育局利用假期在某学习平台组织全区教职工进行网络学习.第
一学习阶段结束后,为了解学习情况,负责人从平台数据库中随机抽取了300名教职工的学习时间(满时
长15小时),将其分成 六组,并绘制成如图所示的频率分布直方
图(同一组中的数据用该组区间的中点值为代表).
参考数据:若随机变量 服从正态分布 ,则 ,
, .
第4页/共6页
学科网(北京)股份有限公司(1)求a的值;
(2)以样本估计总体,该地区教职工学习时间 近似服从正态分布 ,其中 近似为样本的平均
数,经计算知 .若该地区有5000名教职工,试估计该地区教职工中学习时间在 内
的人数;
(3)现采用分层抽样的方法从样本中学习时间在 内的教职工中随机抽取5人,并从中随机抽
取3人作进一步分析,分别求这3人中学习时间在 内的教职工平均人数.(四舍五入取整数)
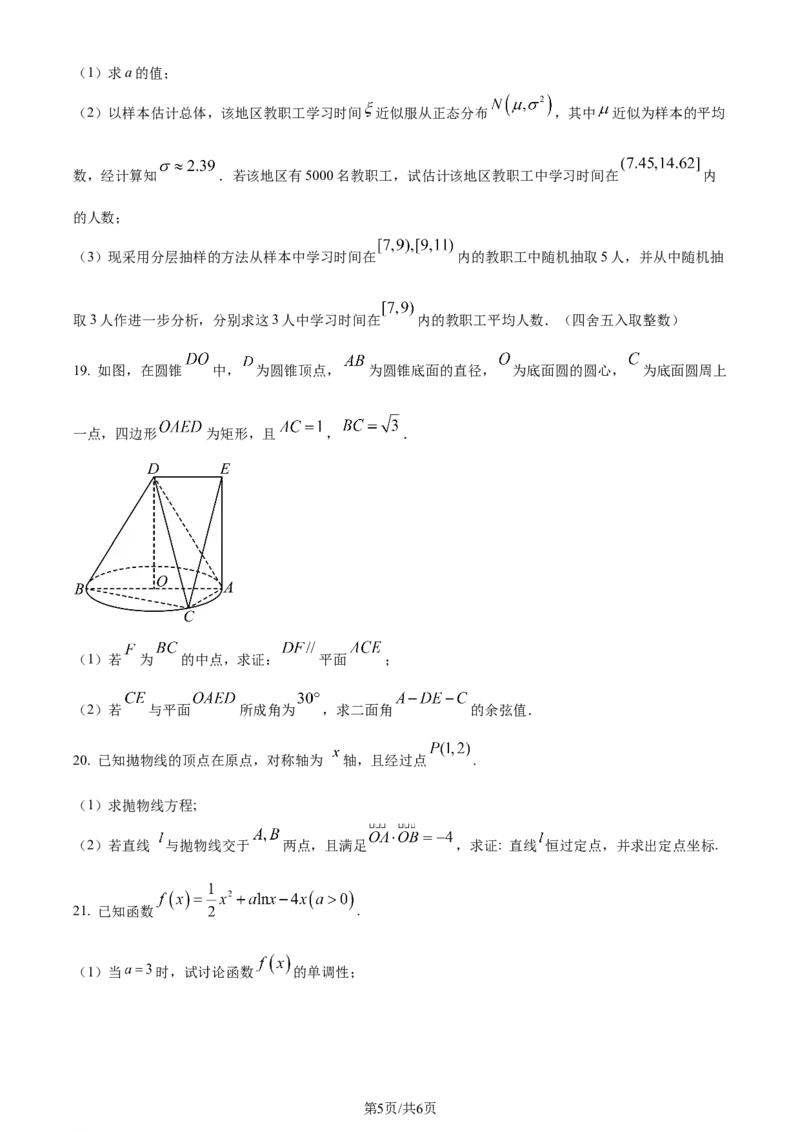
19. 如图,在圆锥 中, 为圆锥顶点, 为圆锥底面的直径, 为底面圆的圆心, 为底面圆周上
一点,四边形 为矩形,且 , .
(1)若 为 的中点,求证: 平面 ;
(2)若 与平面 所成角为 ,求二面角 的余弦值.
20. 已知拋物线的顶点在原点,对称轴为 轴,且经过点 .
(1)求抛物线方程;
(2)若直线 与抛物线交于 两点,且满足 ,求证: 直线 恒过定点,并求出定点坐标.
21. 已知函数 .
(1)当 时,试讨论函数 的单调性;
第5页/共6页
学科网(北京)股份有限公司(2)设函数 有两个极值点 ,证明: .
22. 在平面直角坐标系 中,曲线 参数方程为
的
(1)求曲线 的直角坐标方程;
(2)已知点 ,直线 的参数方程为 ( 为参数, ),且直线 与曲线 交于A、 两
点,求 的值.
第6页/共6页
学科网(北京)股份有限公司