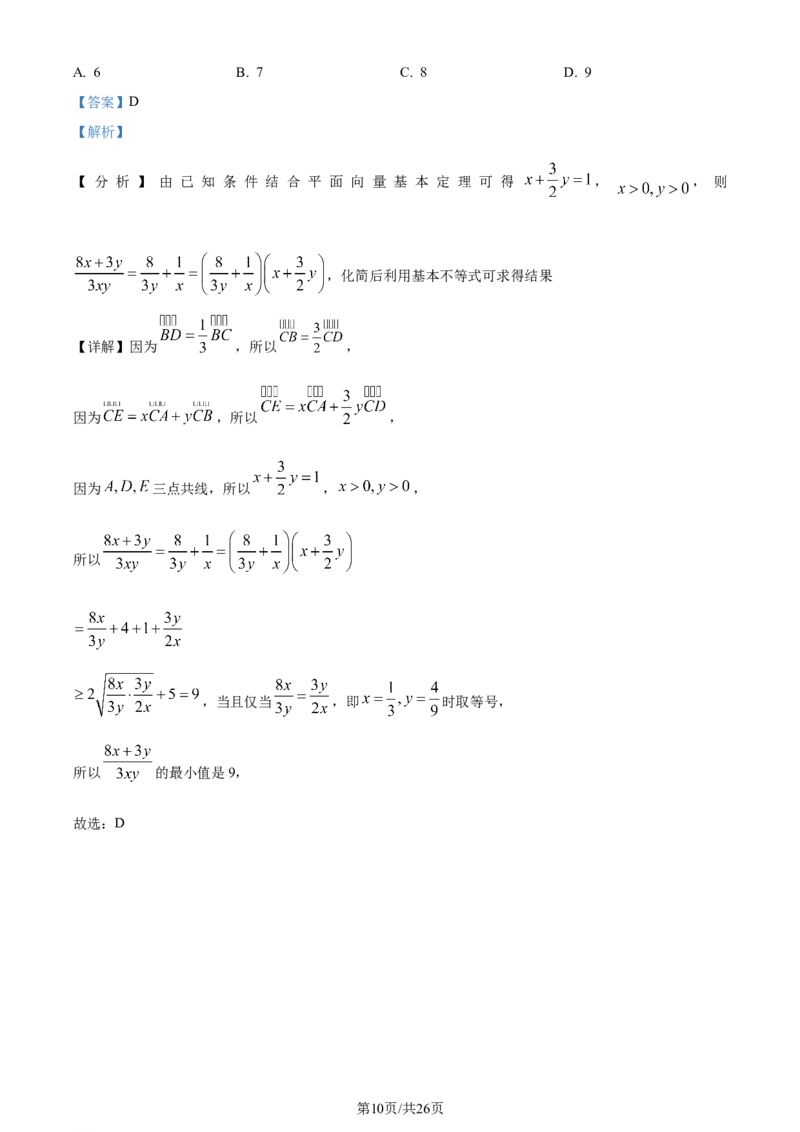文档内容
2023-2024 学年高中毕业班阶段性测试(一)
理科数学
考生注意:
1.答题前,考生务必将自己的姓名、考生号填写在试卷和答题卡上,并将考生号条形码粘贴在
答题卡上的指定位置.
2.回答选择题时,选出每小题答案后,用铅笔把答题卡对应题目的答案标号涂黑.如需改动,
用橡皮擦干净后,再选涂其他答案标号,回答非选择题时,将答案写在答题卡上.写在本试卷
上无效.
3.考试结束后,将本试卷和答题卡一并交回.
一、选择题:本题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是
符合题目要求的.
1. ( )
A. B.
C. D.
【答案】B
【解析】
【分析】根据复数的四则运算法则计算得出结果.
【详解】 .
故选:B.
2. 已知集合 , ,则 ( )
A. B.
第1页/共26页
学科网(北京)股份有限公司C. D.
【答案】D
【解析】
【分析】先结合一元二次不等式解法分别计算集合,再应用交并补定义计算即可.
【详解】 因为 ,
,
则 .
故选:D.
3. 已知函数 ,若 ,则 ( )
A. B. C. D. 10
【答案】A
【解析】
【分析】根据 得到 ,再由 求解.
【详解】解:因为函数 ,
所以 ,
所以 ,
又 ,
所以 ,
故选:A
4. 若实数 满足约束条件 ,则 的最大值为( )
A. 3 B. 7 C. 11 D. 15
第2页/共26页
学科网(北京)股份有限公司【答案】C
【解析】
【分析】首先画出不等式组表示的平面区域,再利用 的几何意义求目标函数的最大值.
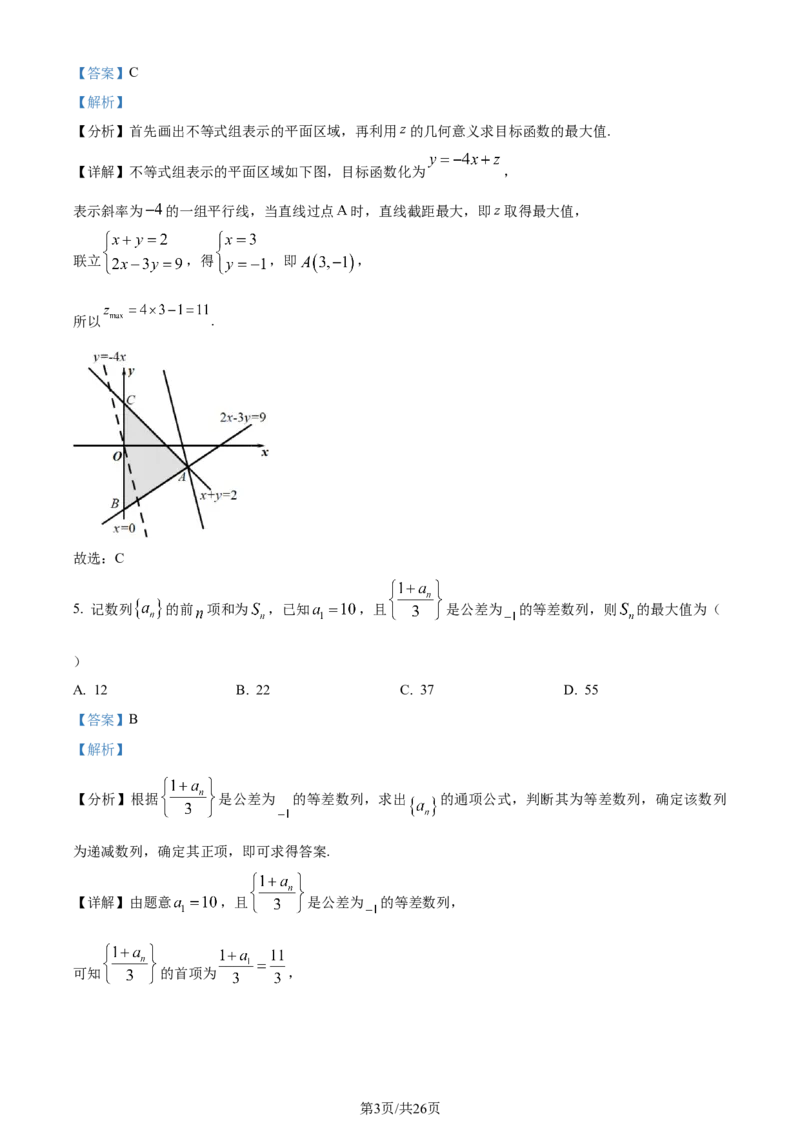
【详解】不等式组表示的平面区域如下图,目标函数化为 ,
表示斜率为 的一组平行线,当直线过点 时,直线截距最大,即 取得最大值,
联立 ,得 ,即 ,
所以 .
故选:C
5. 记数列 的前 项和为 ,已知 ,且 是公差为 的等差数列,则 的最大值为(
)
A. 12 B. 22 C. 37 D. 55
【答案】B
【解析】
【分析】根据 是公差为 的等差数列,求出 的通项公式,判断其为等差数列,确定该数列
为递减数列,确定其正项,即可求得答案.
【详解】由题意 ,且 是公差为 的等差数列,
可知 的首项为 ,
第3页/共26页
学科网(北京)股份有限公司则 ,
故 ,则数列 为 ,公差为 的等差数列,且为递减数列,
令 ,
即等差数列 的前4项为正项,从第5项开始为负,
故 的最大值为 ,
故选:B
6. 对于任意实数 ,用 表示不大于 的最大整数,例如: , , ,则“
”是“ ”的( )
A. 充分不必要条件 B. 必要不充分条件
C. 充分必要条件 D. 既不充分也不必要条件
【答案】A
【解析】
【分析】对任意的 ,记 ,则 ,利用题中定义、不等式的基本性质、特殊值
法结合充分条件、必要条件的定义判断可得出结论.
【详解】对任意的 ,记 ,则 ,
若 ,则 ,即 ,则 ,
因为 , ,则 ,由不等式的基本性质可得 ,
所以, ,所以, ,即 ,
所以,“ ” “ ”;
若 ,如取 , ,则 ,故“ ” “ ”.
第4页/共26页
学科网(北京)股份有限公司因此,“ ”是“ ”的充分不必要条件.
故选:A.
7. 已知函数 ,若将 的图象向左平移 个单位长度后所得的图象关
于坐标原点对称,则m的最小值为( )
A. B. C. D.
【答案】B
【解析】
【分析】先平移得出函数解析式,再根据奇偶性结合范围求参即可.
【详解】 的图象向左平移 m 个单位长度后,得到的图象对应函数
,
因为 的图象关于坐标原点对称,
所以 ,即 ,
因为 ,故当 时,m取得最小值 .
故选:B.
8. 位于成都市龙泉驿区的东安湖体育公园是第31届世界大学生夏季运动会的核心场馆,它包含一座综合
运动场、一座多功能体育馆、一座游泳跳水馆和一座综合小球馆.现安排包含甲、乙在内的6名同学到这
4个场馆做志愿者,每人去1个场馆,每个场馆至少安排1个人,则甲、乙两人安排在相同场馆的方法种
数为( )
第5页/共26页
学科网(北京)股份有限公司A. 96 B. 144 C. 240 D. 360
【答案】C
【解析】
【分析】根据分组方法,结合组合数、排列数等知识求得正确答案.
【详解】先将6名同学分成4组:一种方式是甲、乙组成一组,再从另外 4人任选2人组成一组,其余的
一人一组,
另一种方式是甲、乙与另外4人中的1人组成一组,其余的一人一组.再把4组人分到4个场馆,
所以安排方法种数为 .
故选:C
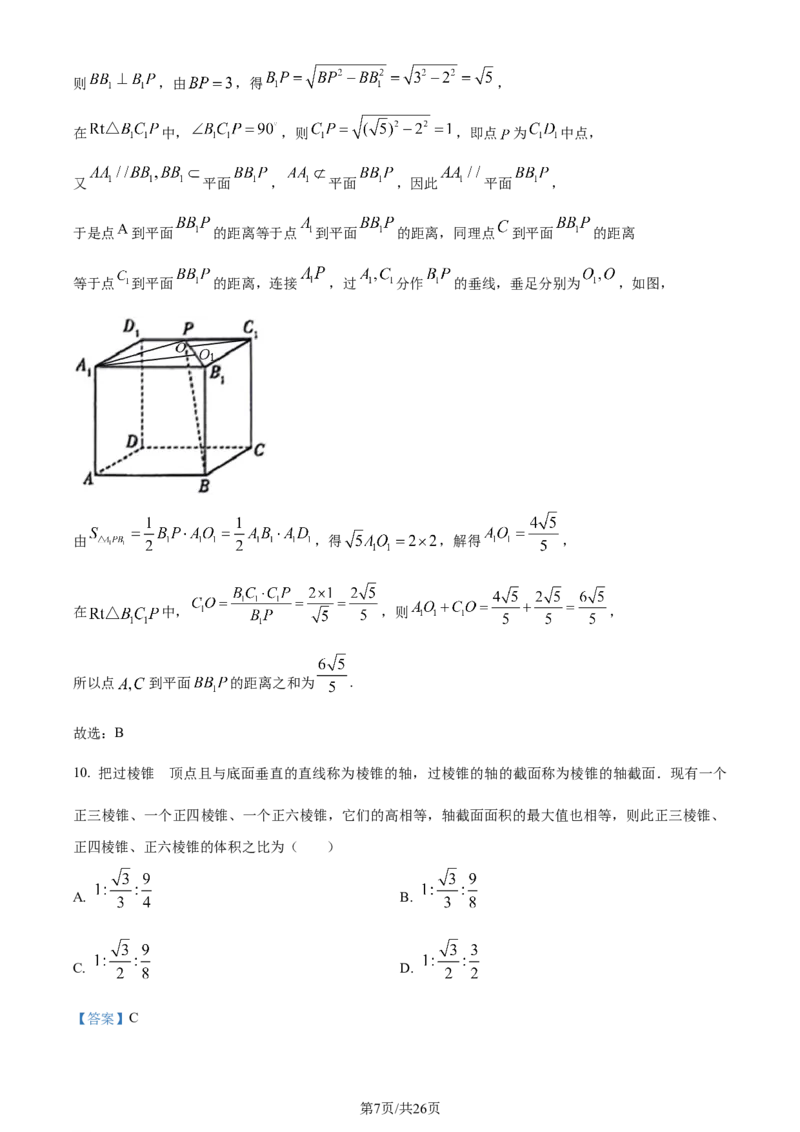
9. 如图所示,在棱长为2的正方体 中,点 在棱 上,且 ,则点 到平
面 的距离之和为( )
A. B. C. D.
【答案】B
【解析】
【分析】根据条件确定点P的位置,利用线面平行把点 到平面 的距离分别转化点 到平面
的距离求解即可.
【详解】在棱长为2的正方体 中, 平面 , 平面 ,
第6页/共26页
学科网(北京)股份有限公司则 ,由 ,得 ,
在 中, ,则 ,即点 为 中点,
又 平面 , 平面 ,因此 平面 ,
于是点 到平面 的距离等于点 到平面 的距离,同理点 到平面 的距离
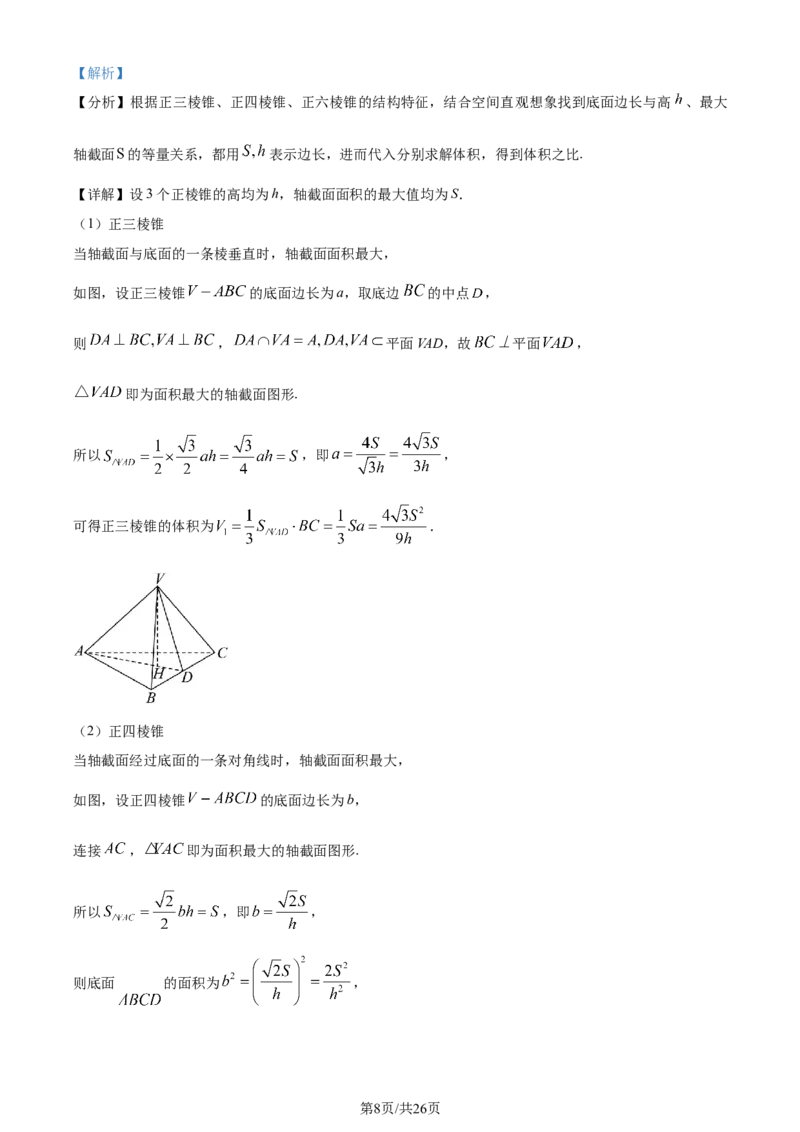
等于点 到平面 的距离,连接 ,过 分作 的垂线,垂足分别为 ,如图,
由 ,得 ,解得 ,
在 中, ,则 ,
所以点 到平面 的距离之和为 .
故选:B
10. 把过棱锥 的顶点且与底面垂直的直线称为棱锥的轴,过棱锥的轴的截面称为棱锥的轴截面.现有一个
正三棱锥、一个正四棱锥、一个正六棱锥,它们的高相等,轴截面面积的最大值也相等,则此正三棱锥、
正四棱锥、正六棱锥的体积之比为( )
A. B.
C. D.
【答案】C
第7页/共26页
学科网(北京)股份有限公司【解析】
【分析】根据正三棱锥、正四棱锥、正六棱锥的结构特征,结合空间直观想象找到底面边长与高 、最大
轴截面 的等量关系,都用 表示边长,进而代入分别求解体积,得到体积之比.
【详解】设3个正棱锥的高均为h,轴截面面积的最大值均为S.
(1)正三棱锥
当轴截面与底面的一条棱垂直时,轴截面面积最大,
如图,设正三棱锥 的底面边长为a,取底边 的中点 ,
则 , 平面VAD,故 平面 ,
即为面积最大的轴截面图形.
所以 ,即 ,
可得正三棱锥的体积为 .
(2)正四棱锥
当轴截面经过底面的一条对角线时,轴截面面积最大,
如图,设正四棱锥 的底面边长为b,
连接 , 即为面积最大的轴截面图形.
所以 ,即 ,
则底面 的面积为 ,
第8页/共26页
学科网(北京)股份有限公司可得正四棱锥的体积为 .
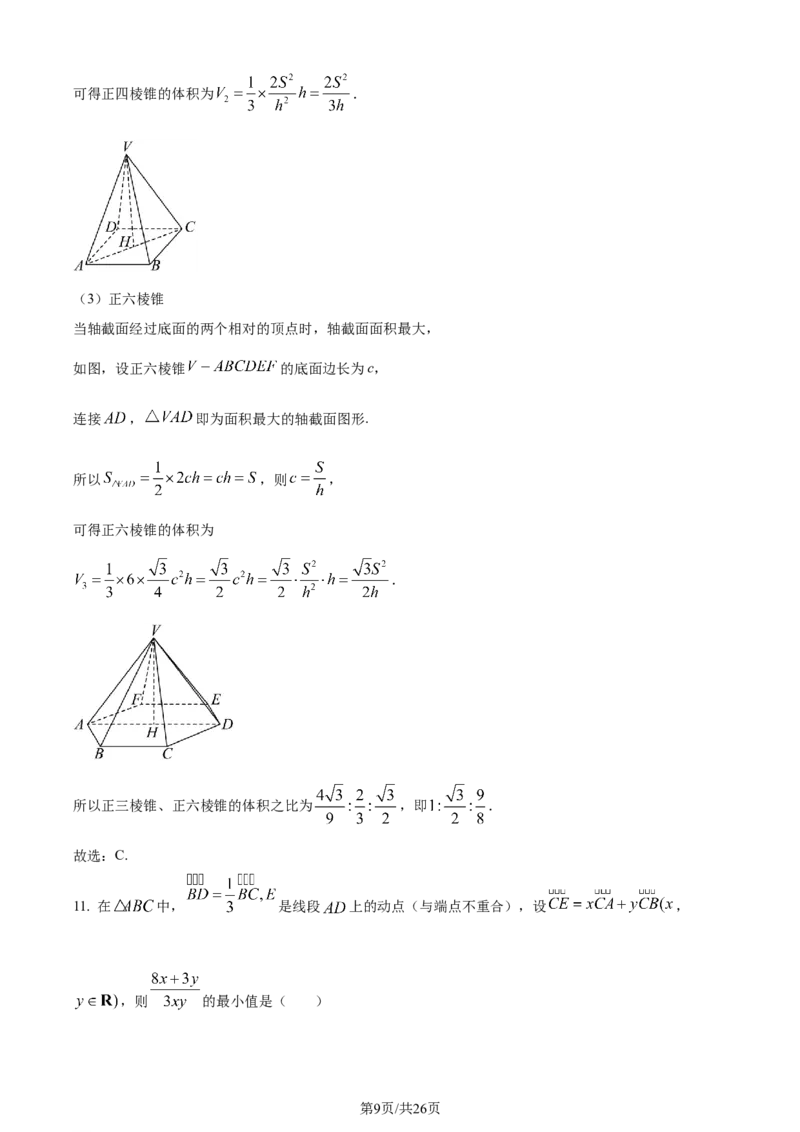
(3)正六棱锥
当轴截面经过底面的两个相对的顶点时,轴截面面积最大,
如图,设正六棱锥 的底面边长为c,
连接 , 即为面积最大的轴截面图形.
所以 ,则 ,
可得正六棱锥的体积为
.
所以正三棱锥、正六棱锥的体积之比为 ,即 .
故选:C.
11. 在 中, 是线段 上的动点(与端点不重合),设 ,
,则 的最小值是( )
第9页/共26页
学科网(北京)股份有限公司A. 6 B. 7 C. 8 D. 9
【答案】D
【解析】
【 分 析 】 由 已 知 条 件 结 合 平 面 向 量 基 本 定 理 可 得 , , 则
,化简后利用基本不等式可求得结果
【详解】因为 ,所以 ,
因为 ,所以 ,
因为 三点共线,所以 , ,
所以
,当且仅当 ,即 时取等号,
所以 的最小值是9,
故选:D
第10页/共26页
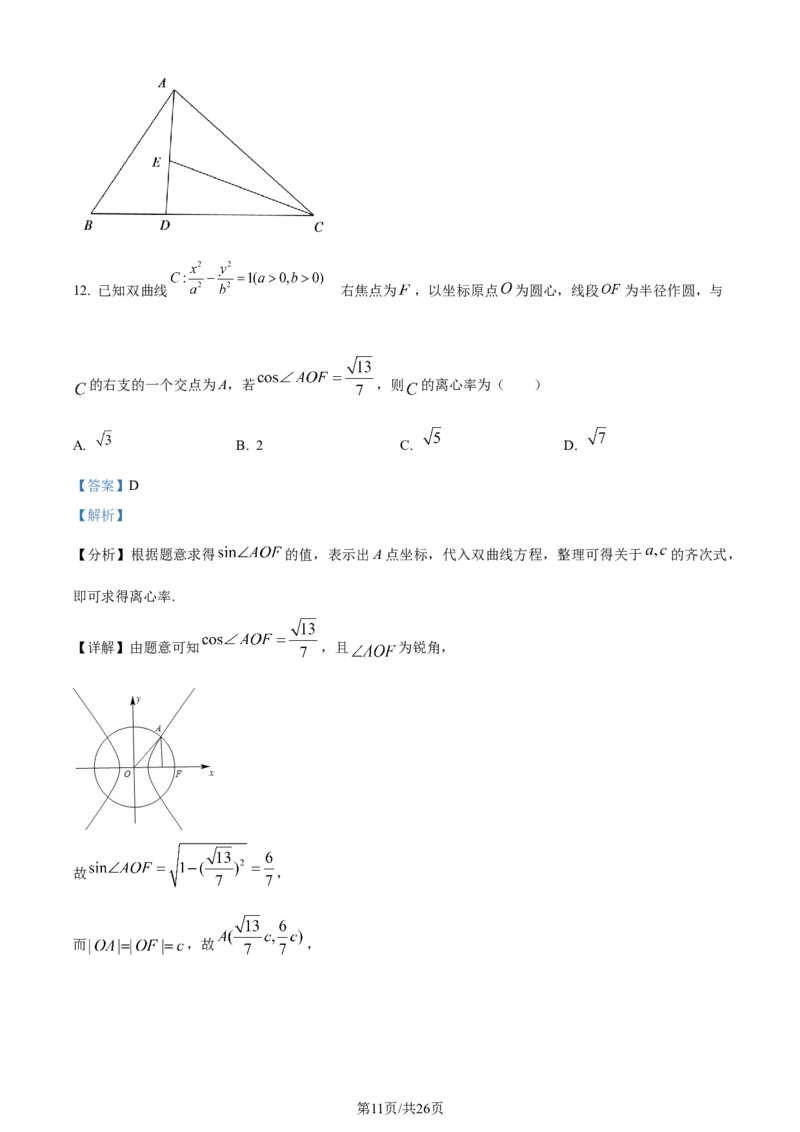
学科网(北京)股份有限公司12. 已知双曲线 的右焦点为 ,以坐标原点 为圆心,线段 为半径作圆,与
的右支的一个交点为A,若 ,则 的离心率为( )
A. B. 2 C. D.
【答案】D
【解析】
【分析】根据题意求得 的值,表示出A点坐标,代入双曲线方程,整理可得关于 的齐次式,
即可求得离心率.
【详解】由题意可知 ,且 为锐角,
故 ,
而 ,故 ,
第11页/共26页
学科网(北京)股份有限公司将 代入 中,
得 ,结合 整理得 ,
即 ,解得 或 ,
由于双曲线离心率 ,故舍去 ,
故 ,
故选:D
二、填空题:本题共4小题,每小题5分,共20分.
13. 已知抛物线 的焦点为 F,直线 与抛物线交于点 M,且 ,则
___________.
【答案】4
【解析】
【分析】求出点M的坐标,利用抛物线的焦半径公式可得关于p的方程,即可求得答案.
【详解】把 代入抛物线方程 ( ),得 ,
得 ,根据抛物线的定义有 ,解得 ,
故答案为:4
14. 某品牌新能源汽车2019-2022年这四年的销量逐年增长,2019年销量为5万辆,2022年销量为22万辆,
且这四年销量的中位数与平均数相等,则这四年的总销量为__________万辆.
【答案】53
【解析】
【分析】根据中位数和平均数公式,结合题意,即可求解.
【详解】设2020年的销量为 ,2021年的销量为 , ,
第12页/共26页
学科网(北京)股份有限公司由题意可知,中位数为 ,平均数为 ,
由 ,得 ,
所以这四年的总销量为 万量.
故答案为:53
15. 已知数列 满足 , ,则满足 的最小正整数 ___________.
【答案】5
【解析】
【分析】根据题意先求得 , ,从而求得 ,再构造等比数列 ,从而得到数列
的通项公式,进而根据 的单调性即可求解.
【详解】由 ,解得 ,
又 ,所以 .
另一方面由 ,可得 ,
所以 是首项为 ,公比为3的等比数列,
所以 ,易知 是递增数列,
又 , ,
所以满足 的最小正整数 .
故答案为:5.
【点睛】本题考查递推数列.
16. 已知定义在R上的函数 及其导函数 满足 ,若 ,则满足不等
第13页/共26页
学科网(北京)股份有限公司式 的x的取值范围是___________.
【答案】
【解析】
【分析】由条件 ,构造函数 ,由 得 在 上单调递增,再
利用单调性解不等式即可.
【详解】由题意,对任意 ,都有 成立,
即 .
构造函数 ,
则 ,
所以函数 在 上单调递增.
不等式 即 ,即 .
因为 ,所以 .
故由 ,得 .
所以不等式 的解集为 ,
故答案为: .
三、解答题:共70 分.解答应写出文字说明,证明过程或演算步骤.第17~21 题为必考题,每
个试题考生都必须作答.第22,23题为选考题,考生根据要求作答.
(一)必考题:共 60 分.
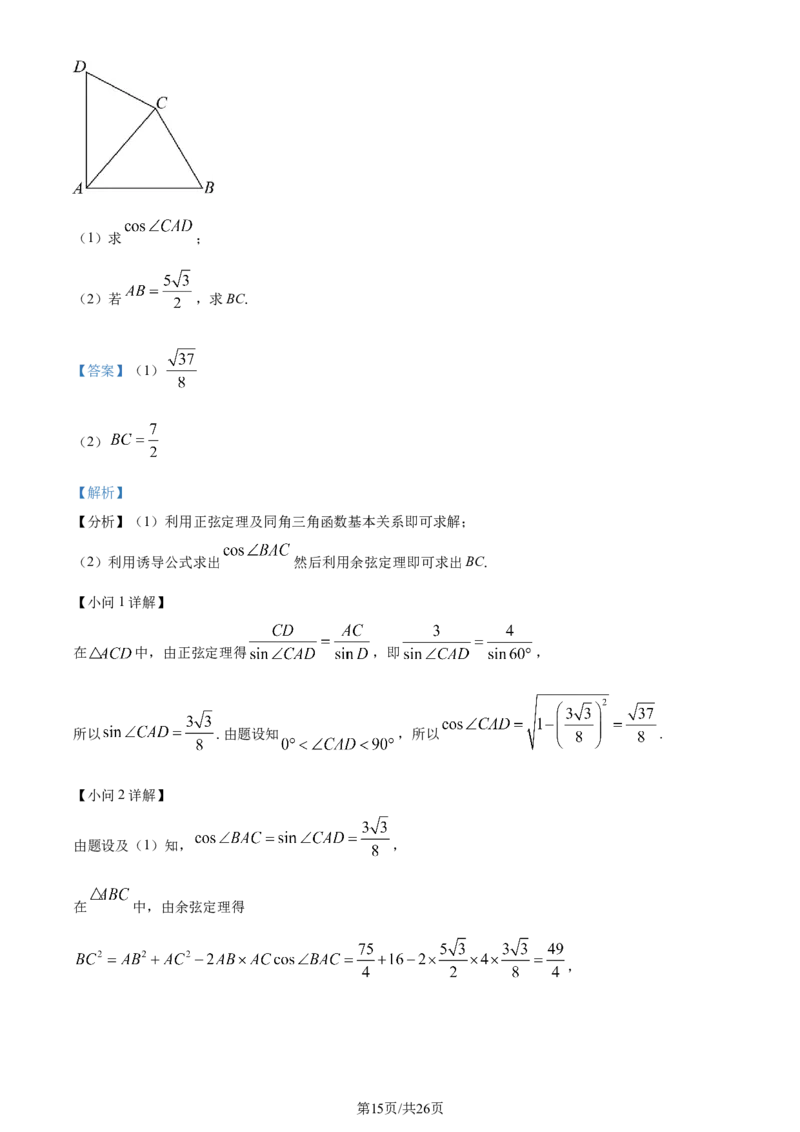
17. 如图,在平面四边形ABCD中, , , , .
第14页/共26页
学科网(北京)股份有限公司(1)求 ;
(2)若 ,求BC.
【答案】(1)
(2)
【解析】
【分析】(1)利用正弦定理及同角三角函数基本关系即可求解;
(2)利用诱导公式求出 然后利用余弦定理即可求出BC.
【小问1详解】
在 中,由正弦定理得 ,即 ,
所以 .由题设知 ,所以 .
【小问2详解】
由题设及(1)知, ,
在 中,由余弦定理得
,
第15页/共26页
学科网(北京)股份有限公司.
所以
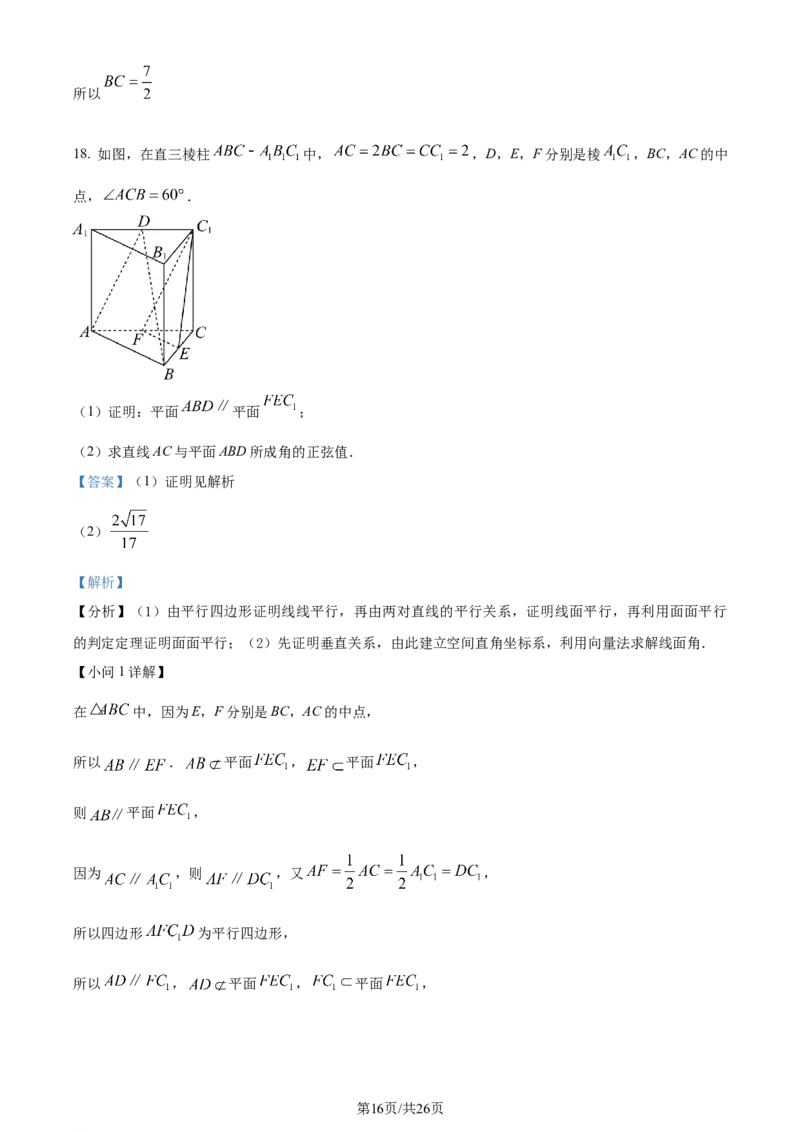
18. 如图,在直三棱柱 中, ,D,E,F分别是棱 ,BC,AC的中
点, .
(1)证明:平面 平面 ;
(2)求直线AC与平面ABD所成角的正弦值.
【答案】(1)证明见解析
(2)
【解析】
【分析】(1)由平行四边形证明线线平行,再由两对直线的平行关系,证明线面平行,再利用面面平行
的判定定理证明面面平行;(2)先证明垂直关系,由此建立空间直角坐标系,利用向量法求解线面角.
【小问1详解】
在 中,因为E,F分别是BC,AC的中点,
所以 . 平面 , 平面 ,
则 平面 ,
因为 ,则 ,又 ,
所以四边形 为平行四边形,
所以 , 平面 , 平面 ,
第16页/共26页
学科网(北京)股份有限公司则 平面 ,
又因为 , 且 平面 ,
所以平面 平面 .
【小问2详解】
因为 , , ,
由余弦定理可得
,
所以 ,从而 .
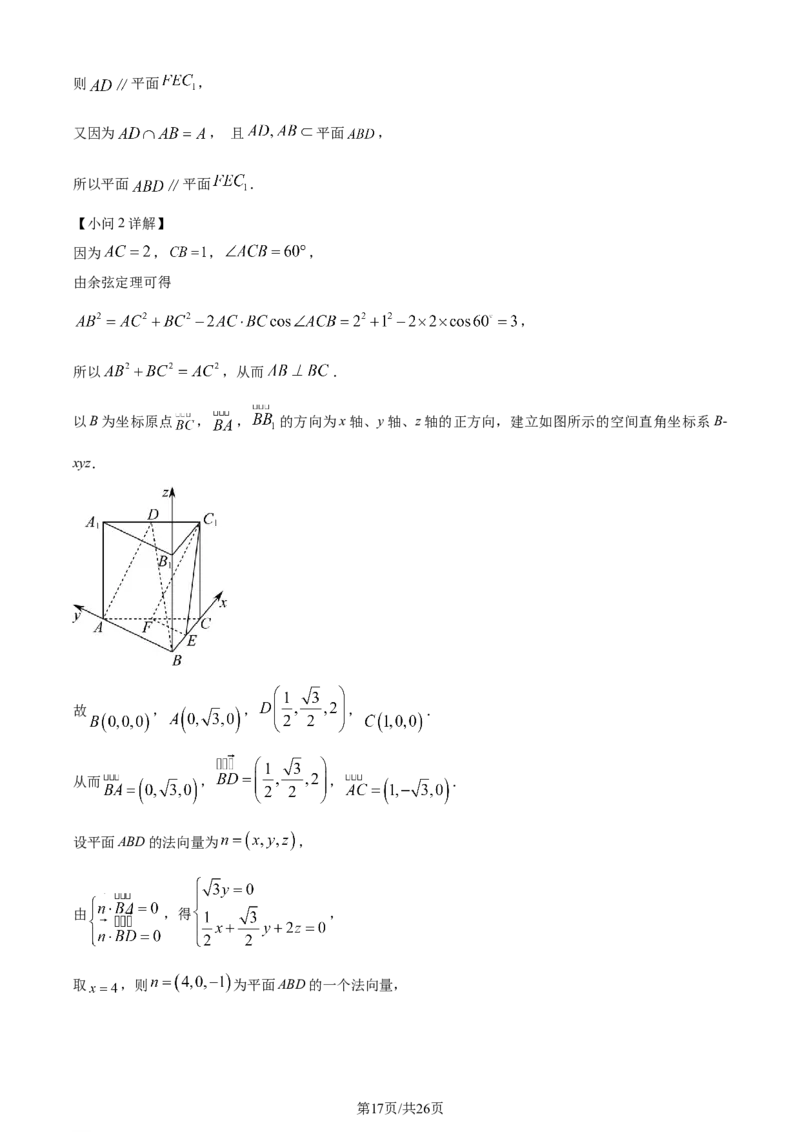
以B为坐标原点 , , 的方向为x轴、y轴、z轴的正方向,建立如图所示的空间直角坐标系B-
xyz.
故 , , , .
从而 , , .
设平面ABD的法向量为 ,
由 ,得 ,
取 ,则 为平面ABD的一个法向量,
第17页/共26页
学科网(北京)股份有限公司所以 ,
所以直线AC与平面ABD所成角的正弦值为 .
19. 已知椭圆C: 过点 ,且C的右焦点为 .
(1)求C的离心率;
(2)过点F且斜率为1的直线与C交于M,N两点,P直线 上的动点,记直线PM,PN,PF的斜率
分别为 , , ,证明: .
【答案】(1)
(2)证明见解析
【解析】
【分析】(1)根据条件求出椭圆方程再求离心率;
(2)设 , , ,将直线MN的方程与椭圆方程联立得 , ,代入斜
率公式验证 成立即可.
【小问1详解】
由 得C的半焦距为 ,所以 ,
又C过点 ,所以 ,解得 ,
所以 , .
故C的离心率为 .
【小问2详解】
第18页/共26页
学科网(北京)股份有限公司由(1)可知C的方程为 .
设 , , .
由题意可得直线MN的方程为 ,
联立 ,消去y可得 ,
则 , ,
则
,
又 ,
因此 .
20. 小李参加某项专业资格考试,一共要考3个科目,若3个科目都合格,则考试直接过关;若都不合格,
则考试不过关;若有1个或2相科目合格,则所有不合格的科目需要进行一次补考,补考都合格的考试过
关,否则不过关.已知小李每个科目每次考试合格的概率均为p( ),且每个科目每次考试的结
第19页/共26页
学科网(北京)股份有限公司果互不影响.
(1)记“小李恰有1个科目需要补考”的概率为 ,求 的最大值点 .
(2)以(1)中确定的 作为p的值.
(ⅰ)求小李这项资格考试过关的概率;
(ⅱ)若每个科目每次考试要缴纳20元的费用,将小李需要缴纳的费用记为X元,求 .
【答案】(1)
(2)(ⅰ) ;(ⅱ)
【解析】
【分析】(1)利用概率的乘法公式可得 ,再根据导数讨论单调性和最值;
(2)(i)分三类情况求解:第一次考试都合格;第一次考试2门合格,1门不合格;第一次考试1门合格,
2门不合格;(ii)根据缴费与补考科目的关系求解.
【小问1详解】
由题意知 , ,
则 ,
当 时, ,
当 时, ,
所以函数 在 单调递增, 单调递减,
所以当 时, 取最大值,即 .
【小问2详解】
第20页/共26页
学科网(北京)股份有限公司(ⅰ)小李第一次考试3个科目都合格的概率为 ,
小李第一次考试有2个科目合格,补考1个科目且合格的概率为 ,
小李第一次考试有1个科目合格,补考2个科目且均合格的概率为 ,
所以小李这项资格考试过关的概率为 .
(ⅱ)X的所有可能取值为60,80,100,
则 , ,
,
故 .
21. 已知函数 , 且 .
(1)若当 时, 恒成立,求m的取值范围;
(2)若 , 且 ,使得 ,求证: .
【答案】(1)
(2)证明见解析
【解析】
【分析】(1)分离参数,构造函数 ,利用导数求出函数的最大值即可得解;
第21页/共26页
学科网(北京)股份有限公司(2)条件转化为 ,原不等式可转化为 ,利用函数单调性转化为
,构造函数 ,利用导数判断单调性即可得解.
【小问1详解】
当 时, ,
所以由 ,可得 .
令 ,则 ,
令 ,则 ,而 ,得 .
故当 时, ,
当 时, ,
故 在 上单调递增,在 上单调递减,
故 ,
所以m的取值范围为 .
【小问2详解】
易知 ,所以 ,等价于 ,等价于 .
不妨设 ,由(1)可知 .
第22页/共26页
学科网(北京)股份有限公司要证 ,即证 ,
又因为 在 上单调递减,
所以需证 ,
即 .
令 ,
则
,
当 时, , ,
所以 ,
则 在 上单调递增,
所以 ,即 ,
因此, .
【点睛】关键点点睛:对条件进行转化为 是解题的第一个关键点,再对要证式子变形,转
第23页/共26页
学科网(北京)股份有限公司化为证明不等式 为第二个关键点,构造函数 ,利用导数证明
在 上单调递增是解题的第三个关键点.
(二)选考题:共10分.请考生在第22,23题中任选一题作答,如果多做,则按所做的第一
题计分.
[选修4-4:坐标系与参数方程]
22. 在平面直角坐标系 中,曲线 的参数方程为 ( 为参数),以原点 为极点,
轴的正半轴为极轴建立极坐标系,直线 的极坐标方程为 .
(1)求曲线 的普通方程和直线 的直角坐标方程;
(2)若直线 与曲线 交于 两点,与 轴交于点 ,求 的值.
【答案】(1) ,
(2)36
【解析】
【分析】(1)根据 消参即可,根据极坐标和直角坐标互化公式即可;
(2)先求出直线 的参数方程 ,联立曲线 的普通方程,由 的几何意义即可求解.
【小问1详解】
由曲线 的参数方程消去参数 ,得普通方程为 .
因为 ,所以 ,将 代入得 .
【小问2详解】
第24页/共26页
学科网(北京)股份有限公司由于直线 与 轴的交点坐标为 ,倾斜角为 ,
所以直线 的参数方程为 ( 为参数),
代入 ,得 ,
设 对应的参数分别为 ,则 ,
所以 .
[选修4-5:不等式选讲]
23. 已知函数 .
(1)求不等式 的解集;
(2)若关于 的不等式 的解集为 ,求实数 的取值范围.
【答案】(1)
(2)
【解析】
【分析】(1)分段讨论解绝对值不等式;
(2) 恒成立问题,先求得 的最小值为 ,再解不等式
即可.
【小问1详解】
由 ,可得 ,
第25页/共26页
学科网(北京)股份有限公司当 时,原不等式可化 为 ,化简得 ,不成立;
当 时,原不等式可化为 ,解得 ,故 ;
当 时,原不等式可化为 ,化简得 ,恒成立,故 .
综上可知 的取值范围为 .
【小问2详解】
因为 ,
当 ,即 时, 取最小值,且最小值为 ,
由题可知关于 的不等式 的解集为 ,即不等式恒成立,
所以 ,
解得 .
故实数 的取值范围是
第26页/共26页
学科网(北京)股份有限公司