文档内容
五年(2019-2023)年高考真题分项汇编
专题 02 函数概念与基本初等函数
函数概念与基本初等函数常考题型一般为选择题,中等难度,属于送分题。一般的出题类型为选择,填空。
对于函数周期与奇偶性以及综合应用一般难度比较大,技巧比较强。
考点 01 函数概念与单调性
1.(2023·全国·统考高考真题)设函数 在区间 上单调递减,则 的取值范围是( )
A. B.
C. D.
【答案】D
【分析】利用指数型复合函数单调性,判断列式计算作答.
【详解】函数 在R上单调递增,而函数 在区间 上单调递减,
则有函数 在区间 上单调递减,因此 ,解得 ,
所以 的取值范围是 .
故选:D
2.(2021·全国·统考高考真题)下列函数中最小值为4的是( )
A. B.C. D.
【答案】C
【分析】根据二次函数的性质可判断 选项不符合题意,再根据基本不等式“一正二定三相等”,即可得
出 不符合题意, 符合题意.
【详解】对于A, ,当且仅当 时取等号,所以其最小值为 ,A不符合
题意;
对于B,因为 , ,当且仅当 时取等号,等号取不到,所以
其最小值不为 ,B不符合题意;
对于C,因为函数定义域为 ,而 , ,当且仅当 ,即 时取
等号,所以其最小值为 ,C符合题意;
对于D, ,函数定义域为 ,而 且 ,如当 , ,D不
符合题意.
故选:C.
【点睛】本题解题关键是理解基本不等式的使用条件,明确“一正二定三相等”的意义,再结合有关函数
的性质即可解出.
3.(2021·全国·高考真题)下列函数中是增函数的为( )
A. B. C. D.
【答案】D
【分析】根据基本初等函数的性质逐项判断后可得正确的选项.
【详解】对于A, 为 上的减函数,不合题意,舍.
对于B, 为 上的减函数,不合题意,舍.
对于C, 在 为减函数,不合题意,舍.
对于D, 为 上的增函数,符合题意,
故选:D.
4.(2020·海南·高考真题)已知函数 在 上单调递增,则 的取值范围是( )
A. B. C. D.
【答案】D【分析】首先求出 的定义域,然后求出 的单调递增区间即可.
【详解】由 得 或
所以 的定义域为
因为 在 上单调递增
所以 在 上单调递增
所以
故选:D
【点睛】在求函数的单调区间时一定要先求函数的定义域.
5.(2020·全国·统考高考真题)设函数 ,则 ( )
A.是奇函数,且在(0,+∞)单调递增 B.是奇函数,且在(0,+∞)单调递减
C.是偶函数,且在(0,+∞)单调递增 D.是偶函数,且在(0,+∞)单调递减
【答案】A
【分析】根据函数的解析式可知函数的定义域为 ,利用定义可得出函数 为奇函数,
再根据函数的单调性法则,即可解出.
【详解】因为函数 定义域为 ,其关于原点对称,而 ,
所以函数 为奇函数.
又因为函数 在 上单调递增,在 上单调递增,
而 在 上单调递减,在 上单调递减,
所以函数 在 上单调递增,在 上单调递增.
故选:A.
【点睛】本题主要考查利用函数的解析式研究函数的性质,属于基础题.
考点 02 函数周期性与奇偶性应用
1.(2023·全国·统考高考真题)若 为偶函数,则 ( ).
A. B.0 C. D.1
【答案】B
【分析】根据偶函数性质,利用特殊值法求出 值,再检验即可.【详解】因为 为偶函数,则 ,解得 ,
当 时, , ,解得 或 ,
则其定义域为 或 ,关于原点对称.
,
故此时 为偶函数.
故选:B.
2.(2020·全国·统考高考真题)设函数 ,则f(x)( )
A.是偶函数,且在 单调递增 B.是奇函数,且在 单调递减
C.是偶函数,且在 单调递增 D.是奇函数,且在 单调递减
【答案】D
【分析】根据奇偶性的定义可判断出 为奇函数,排除AC;当 时,利用函数单调性的性质
可判断出 单调递增,排除B;当 时,利用复合函数单调性可判断出 单调递减,从而
得到结果.
【详解】由 得 定义域为 ,关于坐标原点对称,
又 ,
为定义域上的奇函数,可排除AC;
当 时, ,
在 上单调递增, 在 上单调递减,
在 上单调递增,排除B;
当 时, ,
在 上单调递减, 在定义域内单调递增,根据复合函数单调性可知: 在 上单调递减,D正确.
故选:D.
【点睛】本题考查函数奇偶性和单调性的判断;判断奇偶性的方法是在定义域关于原点对称的前提下,根
据 与 的关系得到结论;判断单调性的关键是能够根据自变量的范围化简函数,根据单调性的性
质和复合函数“同增异减”性得到结论.
3.(2019·全国·高考真题)设 是定义域为 的偶函数,且在 单调递减,则
A.
B.
C.
D.
【答案】C
【解析】由已知函数为偶函数,把 ,转化为同一个单调区间上,再比较大小.
【详解】 是R的偶函数, .
,
又 在(0,+∞)单调递减,
∴ ,
,故选C.
【点睛】本题主要考查函数的奇偶性、单调性,解题关键在于利用中间量大小比较同一区间的取值.
4.(2023·全国·统考高考真题)已知 是偶函数,则 ( )
A. B. C.1 D.2
【答案】D
【分析】根据偶函数的定义运算求解.【详解】因为 为偶函数,则 ,
又因为 不恒为0,可得 ,即 ,
则 ,即 ,解得 .
故选:D.
5.(2022·全国·统考高考真题)已知函数 的定义域均为R,且
.若 的图像关于直线 对称, ,则
( )
A. B. C. D.
【答案】D
【分析】根据对称性和已知条件得到 ,从而得到 ,
,然后根据条件得到 的值,再由题意得到 从而得到 的值
即可求解.
【详解】因为 的图像关于直线 对称,
所以 ,
因为 ,所以 ,即 ,
因为 ,所以 ,
代入得 ,即 ,
所以 ,
.
因为 ,所以 ,即 ,所以 .
因为 ,所以 ,又因为 ,
联立得, ,
所以 的图像关于点 中心对称,因为函数 的定义域为R,
所以
因为 ,所以 .
所以 .
故选:D
【点睛】含有对称轴或对称中心的问题往往条件比较隐蔽,考生需要根据已知条件进行恰当的转化,然后得到所需的一些数值或关系式从而解题.
6.(2022·全国·统考高考真题)已知函数 的定义域为R,且 ,
则 ( )
A. B. C.0 D.1
【答案】A
【分析】法一:根据题意赋值即可知函数 的一个周期为 ,求出函数一个周期中的
的值,即可解出.
【详解】[方法一]:赋值加性质
因为 ,令 可得, ,所以 ,令 可
得, ,即 ,所以函数 为偶函数,令 得,
,即有 ,从而可知 ,
,故 ,即 ,所以函数 的一个周期为 .因为
, , ,
, ,所以
一个周期内的 .由于22除以6余4,
所以 .故选:A.
[方法二]:【最优解】构造特殊函数
由 ,联想到余弦函数和差化积公式
,可设 ,则由方法一中 知 ,
解得 ,取 ,
所以 ,则
,所以
符合条件,因此 的周期 , ,且
,所以 ,
由于22除以6余4,所以 .故选:A.
【整体点评】法一:利用赋值法求出函数的周期,即可解出,是该题的通性通法;
法二:作为选择题,利用熟悉的函数使抽象问题具体化,简化推理过程,直接使用具体函数的性质解题,
简单明了,是该题的最优解.
7.(2021·全国·统考高考真题)设函数 ,则下列函数中为奇函数的是( )
A. B. C. D.
【答案】B
【分析】分别求出选项的函数解析式,再利用奇函数的定义即可.
【详解】由题意可得 ,
对于A, 不是奇函数;
对于B, 是奇函数;
对于C, ,定义域不关于原点对称,不是奇函数;
对于D, ,定义域不关于原点对称,不是奇函数.
故选:B
8.(2021·全国·高考真题)设 是定义域为R的奇函数,且 .若 ,则
( )
A. B. C. D.
【答案】C
【分析】由题意利用函数的奇偶性和函数的递推关系即可求得 的值.
【详解】由题意可得: ,
而 ,
故 .故选:C.
【点睛】关键点点睛:本题主要考查了函数的奇偶性和函数的递推关系式,灵活利用所给的条件进行转化
是解决本题的关键.
9.(2020·山东·统考高考真题)若定义在 的奇函数f(x)在 单调递减,且f(2)=0,则满足
的x的取值范围是( )
A. B.
C. D.
【答案】D
【分析】首先根据函数奇偶性与单调性,得到函数 在相应区间上的符号,再根据两个数的乘积大于等
于零,分类转化为对应自变量不等式,最后求并集得结果.
【详解】因为定义在 上的奇函数 在 上单调递减,且 ,
所以 在 上也是单调递减,且 , ,
所以当 时, ,当 时, ,
所以由 可得:
或 或
解得 或 ,
所以满足 的 的取值范围是 ,
故选:D.
【点睛】本题考查利用函数奇偶性与单调性解抽象函数不等式,考查分类讨论思想方法,属中档题.
二、填空题
10.(2023·全国·统考高考真题)若 为偶函数,则 ________.
【答案】2
【分析】利用偶函数的性质得到 ,从而求得 ,再检验即可得解.
【详解】因为 为偶函数,定义域为 ,
所以 ,即 ,
则 ,故 ,
此时 ,所以 ,
又定义域为 ,故 为偶函数,
所以 .
故答案为:2.
11.(2021·全国·统考高考真题)已知函数 是偶函数,则 ______.
【答案】1
【分析】利用偶函数的定义可求参数 的值.
【详解】因为 ,故 ,
因为 为偶函数,故 ,
时 ,整理得到 ,
故 ,
故答案为:1
考点 03 函数图像应用
一、单选题
1.(2022·全国·统考高考真题)如图是下列四个函数中的某个函数在区间 的大致图像,则该函数是
( )
A. B. C. D.
【答案】A
【分析】由函数图像的特征结合函数的性质逐项排除即可得解.
【详解】设 ,则 ,故排除B;设 ,当 时, ,
所以 ,故排除C;
设 ,则 ,故排除D.
故选:A.
2.(2022·全国·统考高考真题)函数 在区间 的图象大致为( )
A. B.
C. D.
【答案】A
【分析】由函数的奇偶性结合指数函数、三角函数的性质逐项排除即可得解.
【详解】令 ,
则 ,
所以 为奇函数,排除BD;
又当 时, ,所以 ,排除C.
故选:A.
3.(2020·全国·统考高考真题)设函数 在 的图像大致如下图,则f(x)的最小正周
期为( )A. B.
C. D.
【答案】C
【分析】由图可得:函数图象过点 ,即可得到 ,结合 是函数
图象与 轴负半轴的第一个交点即可得到 ,即可求得 ,再利用三角函数周期公式即
可得解.
【详解】由图可得:函数图象过点 ,
将它代入函数 可得:
又 是函数 图象与 轴负半轴的第一个交点,
所以 ,解得:
所以函数 的最小正周期为
故选:C
【点睛】本题主要考查了三角函数的性质及转化能力,还考查了三角函数周期公式,属于中档题.
4.(2019·全国·高考真题)函数f(x)= 在[—π,π]的图像大致为
A. B.
C. D.【答案】D
【分析】先判断函数的奇偶性,得 是奇函数,排除A,再注意到选项的区别,利用特殊值得正确答案.
【详解】由 ,得 是奇函数,其图象关于原点对称.又
.故选D.
【点睛】本题考查函数的性质与图象,渗透了逻辑推理、直观想象和数学运算素养.采取性质法或赋值法,
利用数形结合思想解题.
5.(2019·全国·统考高考真题)函数 在 的图像大致为
A. B.
C. D.
【答案】B
【分析】由分子、分母的奇偶性,易于确定函数为奇函数,由 的近似值即可得出结果.
【详解】设 ,则 ,所以 是奇函数,图象关于原
点成中心对称,排除选项C.又 排除选项D; ,排除选项A,故选B.
【点睛】本题通过判断函数的奇偶性,缩小考察范围,通过计算特殊函数值,最后做出选择.本题较易,
注重了基础知识、基本计算能力的考查.
考点 04 函数性质综合应用
一、单选题1.(2022·全国·统考高考真题)已知函数 的定义域为R,且 ,
则 ( )
A. B. C.0 D.1
【答案】A
【分析】法一:根据题意赋值即可知函数 的一个周期为 ,求出函数一个周期中的
的值,即可解出.
【详解】[方法一]:赋值加性质
因为 ,令 可得, ,所以 ,令 可
得, ,即 ,所以函数 为偶函数,令 得,
,即有 ,从而可知 ,
,故 ,即 ,所以函数 的一个周期为 .因为
, , ,
, ,所以
一个周期内的 .由于22除以6余4,
所以 .故选:A.
[方法二]:【最优解】构造特殊函数
由 ,联想到余弦函数和差化积公式
,可设 ,则由方法一中 知 ,
解得 ,取 ,
所以 ,则
,所以
符合条件,因此 的周期 , ,且
,所以 ,
由于22除以6余4,
所以 .故选:A.【整体点评】法一:利用赋值法求出函数的周期,即可解出,是该题的通性通法;
法二:作为选择题,利用熟悉的函数使抽象问题具体化,简化推理过程,直接使用具体函数的性质解题,
简单明了,是该题的最优解.
2.(2022·全国·统考高考真题)已知函数 的定义域均为R,且
.若 的图像关于直线 对称, ,则
( )
A. B. C. D.
【答案】D
【分析】根据对称性和已知条件得到 ,从而得到 ,
,然后根据条件得到 的值,再由题意得到 从而得到 的值
即可求解.
【详解】因为 的图像关于直线 对称,
所以 ,
因为 ,所以 ,即 ,
因为 ,所以 ,
代入得 ,即 ,
所以 ,
.
因为 ,所以 ,即 ,所以 .
因为 ,所以 ,又因为 ,
联立得, ,
所以 的图像关于点 中心对称,因为函数 的定义域为R,
所以
因为 ,所以 .
所以 .
故选:D
【点睛】含有对称轴或对称中心的问题往往条件比较隐蔽,考生需要根据已知条件进行恰当的转化,然后
得到所需的一些数值或关系式从而解题.3.(2021·全国·统考高考真题)设 ,若 为函数 的极大值点,则( )
A. B. C. D.
【答案】D
【分析】先考虑函数的零点情况,注意零点左右附近函数值是否变号,结合极大值点的性质,对 进行分
类讨论,画出 图象,即可得到 所满足的关系,由此确定正确选项.
【详解】若 ,则 为单调函数,无极值点,不符合题意,故 .
有 和 两个不同零点,且在 左右附近是不变号,在 左右附近是变号的.依题意,
为函数 的极大值点, 在 左右附近都是小于零的.
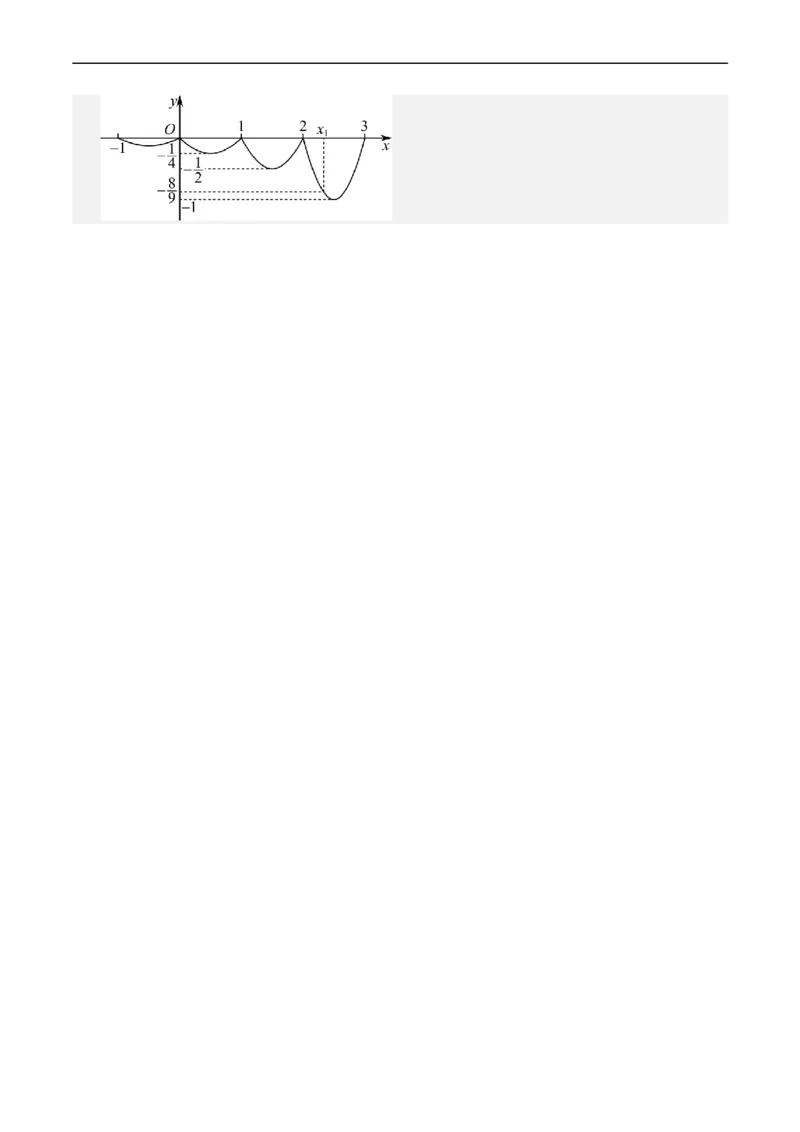
当 时,由 , ,画出 的图象如下图所示:
由图可知 , ,故 .
当 时,由 时, ,画出 的图象如下图所示:
由图可知 , ,故 .
综上所述, 成立.
故选:D
4.(2021·全国·高考真题)设 是定义域为R的奇函数,且 .若 ,则
( )A. B. C. D.
【答案】C
【分析】由题意利用函数的奇偶性和函数的递推关系即可求得 的值.
【详解】由题意可得: ,
而 ,
故 .
故选:C.
【点睛】关键点点睛:本题主要考查了函数的奇偶性和函数的递推关系式,灵活利用所给的条件进行转化
是解决本题的关键.
5.(2021·全国·统考高考真题)设函数 的定义域为R, 为奇函数, 为偶函数,当
时, .若 ,则 ( )
A. B. C. D.
【答案】D
【分析】通过 是奇函数和 是偶函数条件,可以确定出函数解析式 ,进而利
用定义或周期性结论,即可得到答案.
【详解】[方法一]:
因为 是奇函数,所以 ①;
因为 是偶函数,所以 ②.
令 ,由①得: ,由②得: ,
因为 ,所以 ,
令 ,由①得: ,所以 .
思路一:从定义入手.所以 .
[方法二]:
因为 是奇函数,所以 ①;
因为 是偶函数,所以 ②.
令 ,由①得: ,由②得: ,
因为 ,所以 ,
令 ,由①得: ,所以 .
思路二:从周期性入手
由两个对称性可知,函数 的周期 .
所以 .
故选:D.
【点睛】在解决函数性质类问题的时候,我们通常可以借助一些二级结论,求出其周期性进而达到简便计
算的效果.
6.(2021·全国·统考高考真题)已知函数 的定义域为 , 为偶函数, 为奇函数,
则( )
A. B. C. D.
【答案】B
【分析】推导出函数 是以 为周期的周期函数,由已知条件得出 ,结合已知条件可得出结论.
【详解】因为函数 为偶函数,则 ,可得 ,
因为函数 为奇函数,则 ,所以, ,
所以, ,即 ,
故函数 是以 为周期的周期函数,
因为函数 为奇函数,则 ,
故 ,其它三个选项未知.
故选:B.
7.(2020·山东·统考高考真题)若定义在 的奇函数f(x)在 单调递减,且f(2)=0,则满足
的x的取值范围是( )A. B.
C. D.
【答案】D
【分析】首先根据函数奇偶性与单调性,得到函数 在相应区间上的符号,再根据两个数的乘积大于等
于零,分类转化为对应自变量不等式,最后求并集得结果.
【详解】因为定义在 上的奇函数 在 上单调递减,且 ,
所以 在 上也是单调递减,且 , ,
所以当 时, ,当 时, ,
所以由 可得:
或 或
解得 或 ,
所以满足 的 的取值范围是 ,
故选:D.
【点睛】本题考查利用函数奇偶性与单调性解抽象函数不等式,考查分类讨论思想方法,属中档题.
8.(2019·全国·高考真题)设函数 的定义域为R,满足 ,且当 时,
.若对任意 ,都有 ,则m的取值范围是
A. B.
C. D.
【答案】B
【分析】本题为选择压轴题,考查函数平移伸缩,恒成立问题,需准确求出函数每一段解析式,分析出临
界点位置,精准运算得到解决.
【详解】 时, , , ,即 右移1个单位,图像变
为原来的2倍.
如图所示:当 时, ,令 ,整理得:
, (舍), 时, 成立,即
, ,故选B.