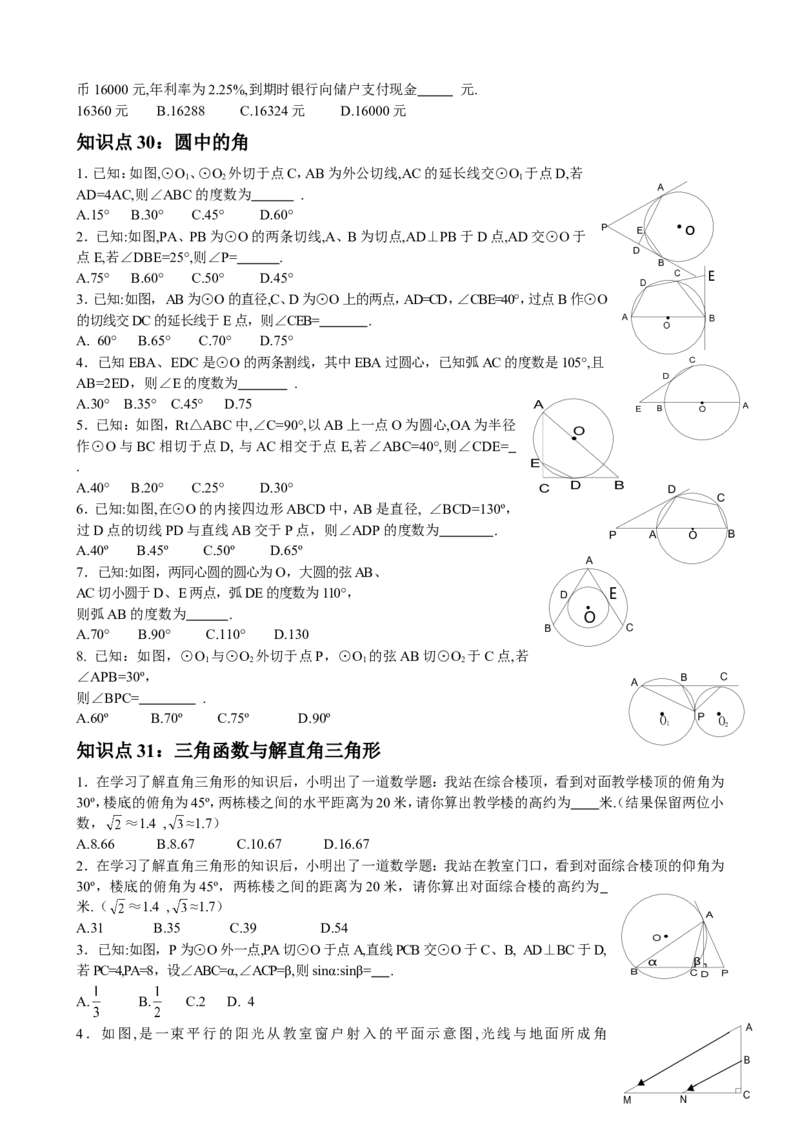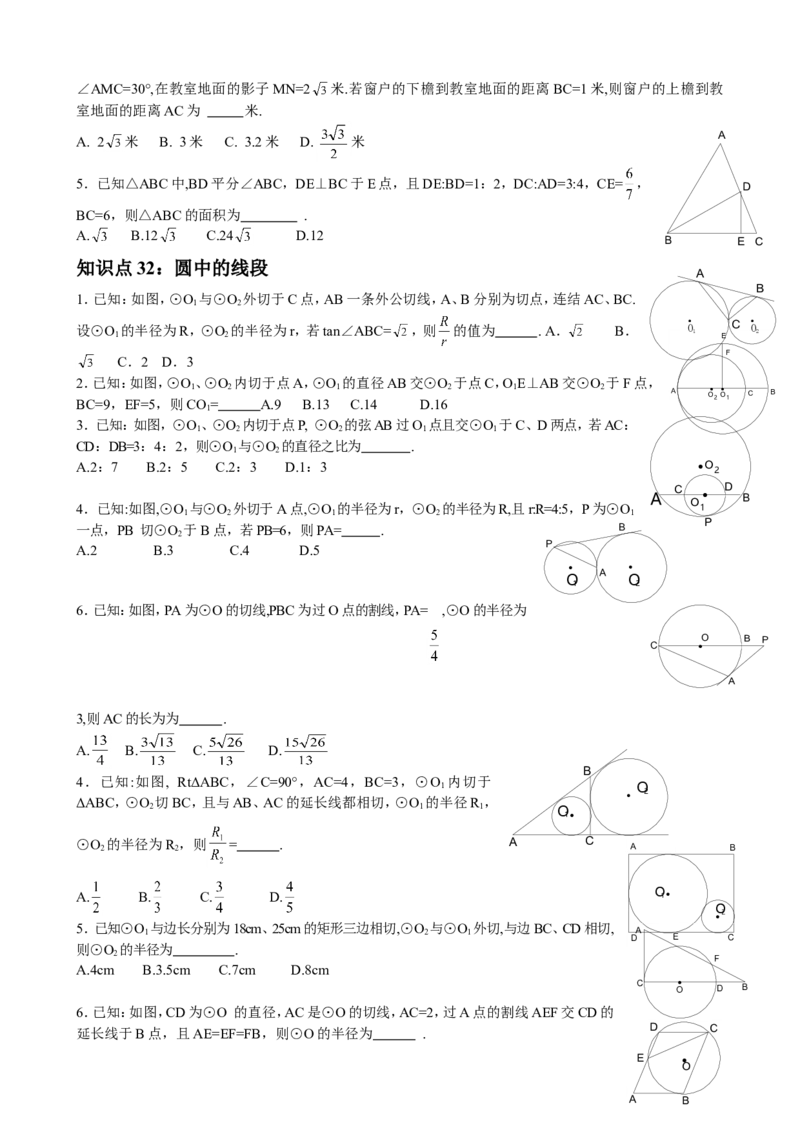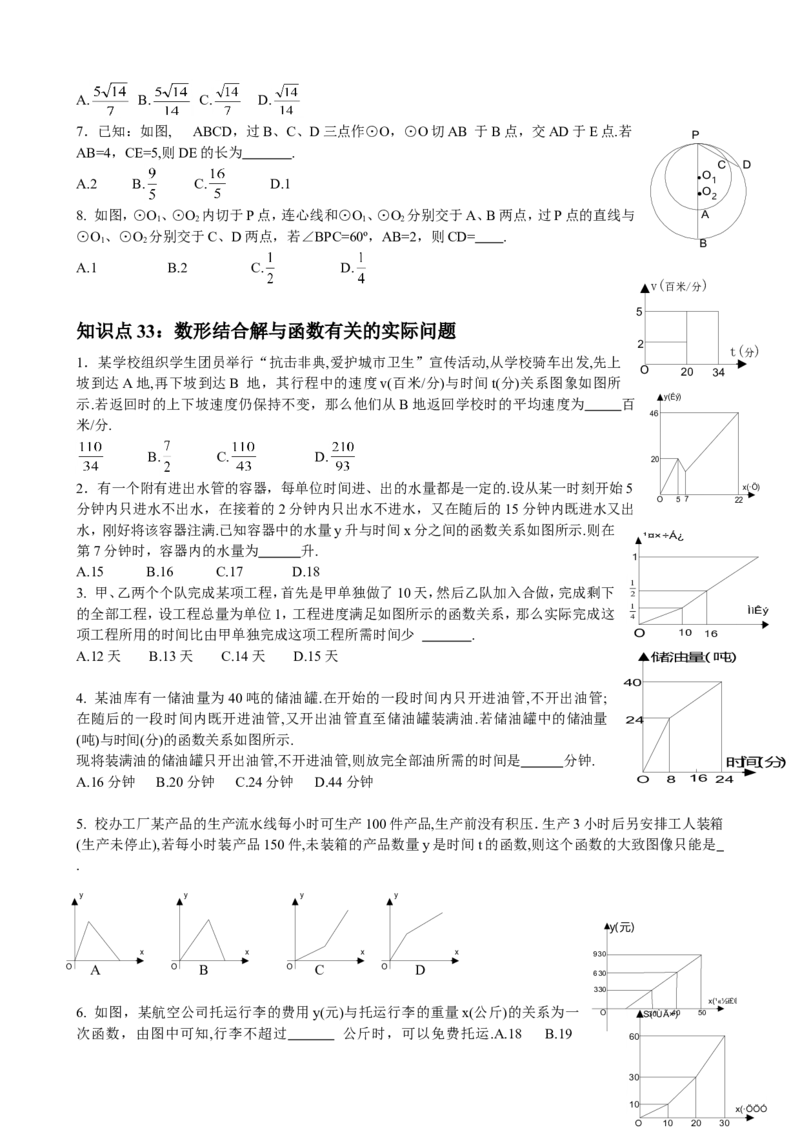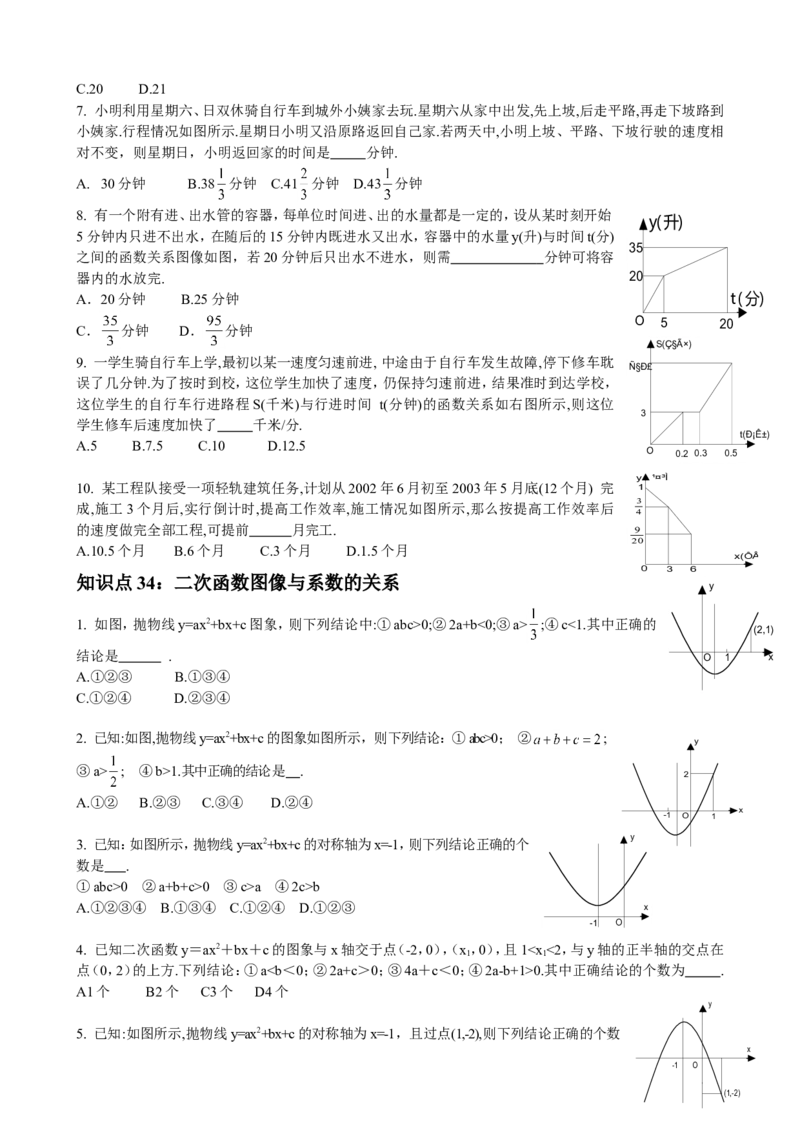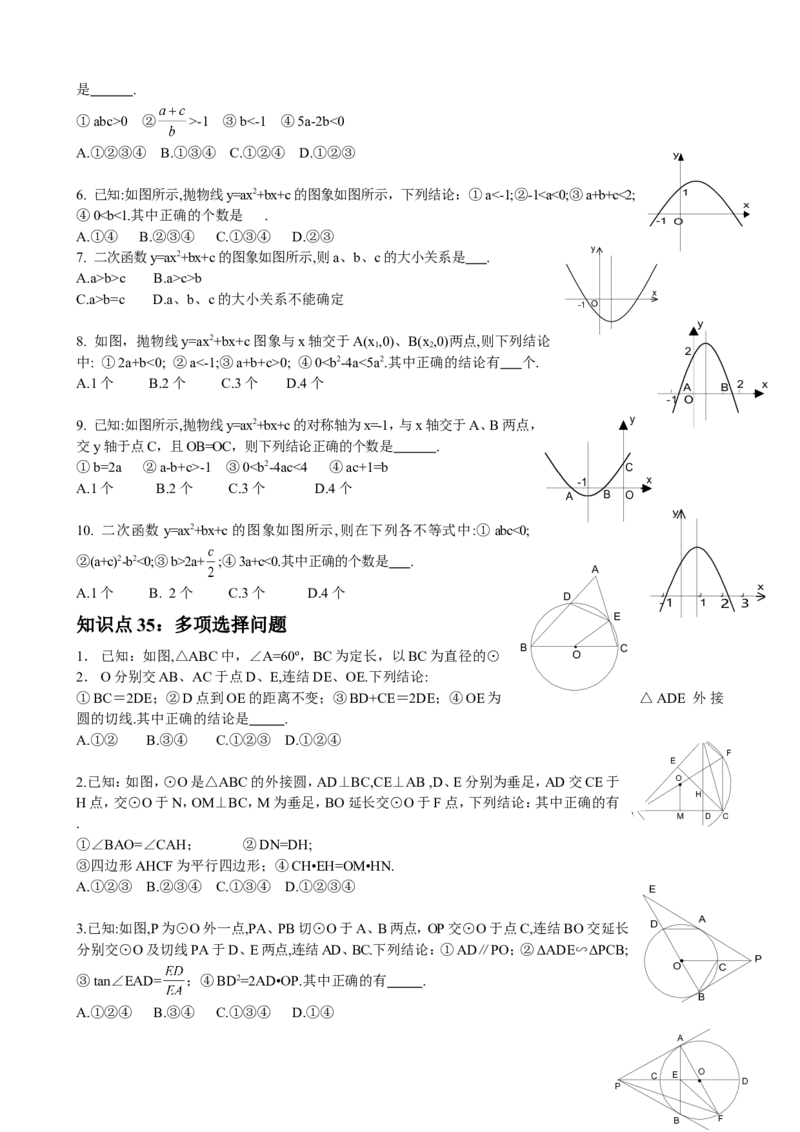文档内容
中考数学重点知识点及重要题型
知识点1:一元二次方程的基本概念
1.一元二次方程3x2+5x-2=0的常数项是-2.
2.一元二次方程3x2+4x-2=0的一次项系数为4,常数项是-2.
3.一元二次方程3x2-5x-7=0的二次项系数为3,常数项是-7.
4.把方程3x(x-1)-2=-4x化为一般式为3x2-x-2=0.
知识点2:直角坐标系与点的位置
1.直角坐标系中,点A(3,0)在y轴上。
2.直角坐标系中,x轴上的任意点的横坐标为0.
3.直角坐标系中,点A(1,1)在第一象限.
4.直角坐标系中,点A(-2,3)在第四象限.
5.直角坐标系中,点A(-2,1)在第二象限.
知识点3:已知自变量的值求函数值
1.当x=2时,函数y= 的值为1.
2.当x=3时,函数y= 的值为1.
3.当x=-1时,函数y= 的值为1.
知识点4:基本函数的概念及性质
1.函数y=-8x是一次函数.
2.函数y=4x+1是正比例函数.
3.函数 是反比例函数.
4.抛物线y=-3(x-2)2-5的开口向下.
5.抛物线y=4(x-3)2-10的对称轴是x=3.
6.抛物线 的顶点坐标是(1,2).
7.反比例函数 的图象在第一、三象限.
知识点5:数据的平均数中位数与众数
1.数据13,10,12,8,7的平均数是10.
2.数据3,4,2,4,4的众数是4.
3.数据1,2,3,4,5的中位数是3.
知识点6:特殊三角函数值
1.cos30°= .
2.sin260°+ cos260°= 1.
3.2sin30°+ tan45°= 2.
4.tan45°= 1.5.cos60°+ sin30°= 1.
知识点7:圆的基本性质
1.半圆或直径所对的圆周角是直角.
2.任意一个三角形一定有一个外接圆.
3.在同一平面内,到定点的距离等于定长的点的轨迹,是以定点为圆心,定长为半径的圆.
4.在同圆或等圆中,相等的圆心角所对的弧相等.
5.同弧所对的圆周角等于圆心角的一半.
6.同圆或等圆的半径相等.
7.过三个点一定可以作一个圆.
8.长度相等的两条弧是等弧.
9.在同圆或等圆中,相等的圆心角所对的弧相等.
10.经过圆心平分弦的直径垂直于弦。
知识点8:直线与圆的位置关系
1.直线与圆有唯一公共点时,叫做直线与圆相切.
2.三角形的外接圆的圆心叫做三角形的外心.
3.弦切角等于所夹的弧所对的圆心角.
4.三角形的内切圆的圆心叫做三角形的内心.
5.垂直于半径的直线必为圆的切线.
6.过半径的外端点并且垂直于半径的直线是圆的切线.
7.垂直于半径的直线是圆的切线.
8.圆的切线垂直于过切点的半径.
知识点9:圆与圆的位置关系
1.两个圆有且只有一个公共点时,叫做这两个圆外切.
2.相交两圆的连心线垂直平分公共弦.
3.两个圆有两个公共点时,叫做这两个圆相交.
4.两个圆内切时,这两个圆的公切线只有一条.
5.相切两圆的连心线必过切点.
知识点10:正多边形基本性质
1.正六边形的中心角为60°.
2.矩形是正多边形.
3.正多边形都是轴对称图形.
4.正多边形都是中心对称图形.
知识点11:一元二次方程的解
1.方程 的根为 .
A.x=2 B.x=-2 C.x=2,x=-2 D.x=4
1 2
2.方程x2-1=0的两根为 .
A.x=1 B.x=-1 C.x=1,x=-1 D.x=2
1 2
3.方程(x-3)(x+4)=0的两根为 .
A.x =-3,x=4 B.x =-3,x=-4 C.x =3,x=4 D.x =3,x=-4
1 2 1 2 1 2 1 2
4.方程x(x-2)=0的两根为 .
A.x=0,x=2 B.x=1,x=2 C.x=0,x=-2 D.x=1,x=-2
1 2 1 2 1 2 1 25.方程x2-9=0的两根为 .
A.x=3 B.x=-3 C.x=3,x=-3 D.x=+ ,x=-
1 2 1 2
知识点12:方程解的情况及换元法
1.一元二次方程 的根的情况是 .
A.有两个相等的实数根 B.有两个不相等的实数根
C.只有一个实数根 D.没有实数根
2.不解方程,判别方程3x2-5x+3=0的根的情况是 .
A.有两个相等的实数根 B. 有两个不相等的实数根
C.只有一个实数根 D. 没有实数根
3.不解方程,判别方程3x2+4x+2=0的根的情况是 .
A.有两个相等的实数根 B. 有两个不相等的实数根
C.只有一个实数根 D. 没有实数根
4.不解方程,判别方程4x2+4x-1=0的根的情况是 .
A.有两个相等的实数根 B.有两个不相等的实数根
C.只有一个实数根 D.没有实数根
5.不解方程,判别方程5x2-7x+5=0的根的情况是 .
A.有两个相等的实数根 B. 有两个不相等的实数根
C.只有一个实数根 D. 没有实数根
6.不解方程,判别方程5x2+7x=-5的根的情况是 .
A.有两个相等的实数根 B. 有两个不相等的实数根
C.只有一个实数根 D. 没有实数根
7.不解方程,判别方程x2+4x+2=0的根的情况是 .
A.有两个相等的实数根 B. 有两个不相等的实数根
C.只有一个实数根 D. 没有实数根
8. 不解方程,判断方程5y +1=2 y的根的情况是
A.有两个相等的实数根 B. 有两个不相等的实数根
C.只有一个实数根 D. 没有实数根
9. 用 换 元 法 解方 程 时, 令 = y,于是原方程变为 .
A.y -5y+4=0 B.y -5y-4=0 C.y -4y-5=0 D.y +4y-5=0
10. 用换元法解方程 时,令 = y ,于是原方程变为 .
A.5y -4y+1=0 B.5y -4y-1=0 C.-5y -4y-1=0 D. -5y -4y-1=0
11. 用换元法解方程( )2-5( )+6=0时,设 =y,则原方程化为关于y的方程是 .
A.y2+5y+6=0 B.y2-5y+6=0 C.y2+5y-6=0 D.y2-5y-6=0
知识点13:自变量的取值范围
1.函数 中,自变量x的取值范围是 .
A.x≠2 B.x≤-2 C.x≥-2 D.x≠-22.函数y= 的自变量的取值范围是 .
A.x>3 B. x≥3 C. x≠3 D. x为任意实数
3.函数y= 的自变量的取值范围是 .
A.x≥-1 B. x>-1 C. x≠1 D. x≠-1
4.函数y= 的自变量的取值范围是 .
A.x≥1 B.x≤1 C.x≠1 D.x为任意实数
5.函数y= 的自变量的取值范围是 .
A.x>5 B.x≥5 C.x≠5 D.x为任意实数
知识点14:基本函数的概念
1.下列函数中,正比例函数是 .
A. y=-8x B.y=-8x+1 C.y=8x2+1 D.y=
2.下列函数中,反比例函数是 .
A. y=8x2 B.y=8x+1 C.y=-8x D.y=-
3.下列函数:①y=8x2;②y=8x+1;③y=-8x;④y=- .其中,一次函数有 个 .
A.1个 B.2个 C.3个 D.4个
A
知识点15:圆的基本性质
O
•
1.如图,四边形ABCD内接于⊙O,已知∠C=80°,则∠A的度数是 . A
A. 50° B. 80° B D
C
C. 90° D. 100° •
O
2.已知:如图,⊙O中, 圆周角∠BAD=50°,则圆周角∠BCD的度数是 .
A B D
A.100° B.130° C.80° D.50° C
3.已知:如图,⊙O中, 圆心角∠BOD=100°,则圆周角∠BCD的度数是 • .
O
A.100° B.130° C.80° D.50°
B D
4.已知:如图,四边形ABCD内接于⊙O,则下列结论中正确的是 .
C
A.∠A+∠C=180° B.∠A+∠C=90°
D
A
C.∠A+∠B=180° D.∠A+∠B=90 A
5.半径为5cm的圆中,有一条长为6cm的弦,则圆心到此弦的距离为 . O• O
A.3cm B.4cm C.5cm D.6cm B C
•
6.已知:如图,圆周角∠BAD=50°,则圆心角∠BOD的度数是 . B D
C
A.100° B.130° C.80° D.50 A
C
7.已知:如图,⊙O中,弧AB的度数为100°,则圆周角∠ACB的度数是 .
O
A.100° B.130° C.200° D.50
•
O
8. 已知:如图,⊙O中, 圆周角∠BCD=130°,则圆心角∠BOD的度数是 .
•
B D
C
A.100° B.130° C.80° D.50° A B
9. 在⊙O中,弦AB的长为8cm,圆心O到AB的距离为3cm,则⊙O的半径为
C
cm.
A.3 B.4 C.5 D. 10
O
•
A B10. 已知:如图,⊙O中,弧AB的度数为100°,则圆周角∠ACB的度数是 .
A.100° B.130° C.200° D.50°
12.在半径为5cm的圆中,有一条弦长为6cm,则圆心到此弦的距离为 .
A. 3cm B. 4 cm C.5 cm D.6 cm
知识点16:点、直线和圆的位置关系
1.已知⊙O的半径为10㎝,如果一条直线和圆心O的距离为10㎝,那么这条直线和这个圆的位置关系为
.
A.相离 B.相切 C.相交 D.相交或相离
2.已知圆的半径为6.5cm,直线l和圆心的距离为7cm,那么这条直线和这个圆的位置关系是 .
A.相切 B.相离 C.相交 D. 相离或相交
3.已知圆O的半径为6.5cm,PO=6cm,那么点P和这个圆的位置关系是
A.点在圆上 B. 点在圆内 C. 点在圆外 D.不能确定
4.已知圆的半径为6.5cm,直线l和圆心的距离为4.5cm,那么这条直线和这个圆的公共点的个数是 .
A.0个 B.1个 C.2个 D.不能确定
5.一个圆的周长为a cm,面积为a cm2,如果一条直线到圆心的距离为πcm,那么这条直线和这个圆的位置
关系是 .
A.相切 B.相离 C.相交 D. 不能确定
6.已知圆的半径为6.5cm,直线l和圆心的距离为6cm,那么这条直线和这个圆的位置关系是 .
A.相切 B.相离 C.相交 D.不能确定
7. 已知圆的半径为6.5cm,直线l和圆心的距离为4cm,那么这条直线和这个圆的位置关系是 .
A.相切 B.相离 C.相交 D. 相离或相交
8. 已知⊙O的半径为7cm,PO=14cm,则PO的中点和这个圆的位置关系是 .
A.点在圆上 B. 点在圆内 C. 点在圆外 D.不能确定
知识点18:公切线问题
1.如果两圆外离,则公切线的条数为 .
A. 1条 B.2条 C.3条 D.4条
2.如果两圆外切,它们的公切线的条数为 .
A. 1条 B. 2条 C.3条 D.4条
3.如果两圆相交,那么它们的公切线的条数为 .
A. 1条 B. 2条 C.3条 D.4条
4.如果两圆内切,它们的公切线的条数为 .
A. 1条 B. 2条 C.3条 D.4条
5. 已知⊙O、⊙O 的半径分别为3cm和4cm,若OO=9cm,则这两个圆的公切线有 条.
1 2 1 2
A.1条 B. 2条 C. 3条 D. 4条
6.已知⊙O、⊙O 的半径分别为3cm和4cm,若OO=7cm,则这两个圆的公切线有 条.
1 2 1 2
A.1条 B. 2条 C. 3条 D. 4条
知识点19:正多边形和圆
1.如果⊙O的周长为10πcm,那么它的半径为 .
A. 5cm B. cm C.10cm D.5πcm
2.正三角形外接圆的半径为2,那么它内切圆的半径为 .
A. 2 B. C.1 D.3.已知,正方形的边长为2,那么这个正方形内切圆的半径为 .
A. 2 B. 1 C. D.
4.扇形的面积为 ,半径为2,那么这个扇形的圆心角为= .
A.30° B.60° C.90° D. 120°
5.已知,正六边形的半径为R,那么这个正六边形的边长为 .
A. R B.R C. R D.
6.圆的周长为C,那么这个圆的面积S= .
A. B. C. D.
7.正三角形内切圆与外接圆的半径之比为 .
A.1:2 B.1: C. :2 D.1:
8. 圆的周长为C,那么这个圆的半径R= .
A.2 B. C. D.
9.已知,正方形的边长为2,那么这个正方形外接圆的半径为 .
A.2 B.4 C.2 D.2
10.已知,正三角形的半径为3,那么这个正三角形的边长为 .
A. 3 B. C.3 D.3
知识点20:函数图像问题
1.已知:关于x的一元二次方程 的一个根为 ,且二次函数 的对称轴是
直线x=2,则抛物线的顶点坐标是 .
A. (2,-3) B. (2,1) C. (2,3) D. (3,2)
2.若抛物线的解析式为y=2(x-3)2+2,则它的顶点坐标是 .
A.(-3,2) B.(-3,-2) C.(3,2) D.(3,-2)
3.一次函数y=x+1的图象在 .
A.第一、二、三象限 B. 第一、三、四象限
C. 第一、二、四象限 D. 第二、三、四象限
4.函数y=2x+1的图象不经过 .
A.第一象限 B. 第二象限 C. 第三象限 D. 第四象限
5.反比例函数y= 的图象在 .
A.第一、二象限 B. 第三、四象限 C. 第一、三象限 D. 第二、四象限
6.反比例函数y=- 的图象不经过 .
A第一、二象限 B. 第三、四象限 C. 第一、三象限 D. 第二、四象限
7.若抛物线的解析式为y=2(x-3)2+2,则它的顶点坐标是 .
A.(-3,2) B.(-3,-2) C.(3,2) D.(3,-2)
8.一次函数y=-x+1的图象在 .
A.第一、二、三象限 B. 第一、三、四象限
C. 第一、二、四象限 D. 第二、三、四象限
9.一次函数y=-2x+1的图象经过 .
A.第一、二、三象限 B.第二、三、四象限C.第一、三、四象限 D.第一、二、四象限
10. 已知抛物线y=ax2+bx+c(a>0且a、b、c为常数)的对称轴为x=1,且函数图象上有三点A(-1,y )、B( ,y)、
1 2
C(2,y ),则y、y、y 的大小关系是 .
3 1 2 3
A.y 0,化简二次根式 的正确结果为 .
A. B. C.- D.-
2.化简二次根式 的结果是 .
A. B.- C. D.
3.若aa,化简二次根式a2 的结果是 .
A. B. C. D.
10.化简二次根式 的结果是 .
A. B.- C. D.
11.若ab<0,化简二次根式 的结果是 .
A.b B.-b C. b D. -b
知识点23:方程的根
1.当m= 时,分式方程 会产生增根.
A.1 B.2 C.-1 D.22.分式方程 的解为 .
A.x=-2或x=0 B.x=-2 C.x=0 D.方程无实数根
3.用换元法解方程 ,设 =y,则原方程化为关于y的方程 .
A.y +2y-5=0 B.y +2y-7=0 C.y +2y-3=0 D.y +2y-9=0
4.已知方程(a-1)x2+2ax+a2+5=0有一个根是x=-3,则a的值为 .
A.-4 B. 1 C.-4或1 D.4或-1
5.关于x的方程 有增根,则实数a为 .
A.a=1 B.a=-1 C.a=±1 D.a= 2
6.二次项系数为1的一元二次方程的两个根分别为- - 、 - ,则这个方程是 .
A.x +2 x-1=0 B.x +2 x+1=0
C.x -2 x-1=0 D.x -2 x+1=0
7.已知关于x的一元二次方程(k-3)x2-2kx+k+1=0有两个不相等的实数根,则k的取值范围是 .
A.k>- B.k>- 且k≠3 C.k<- D.k> 且k≠3
知识点24:求点的坐标
1.已知点P的坐标为(2,2),PQ‖x轴,且PQ=2,则Q点的坐标是 .
A.(4,2) B.(0,2)或(4,2) C.(0,2) D.(2,0)或(2,4)
2.如果点P到x轴的距离为3,到y轴的距离为4,且点P在第四象限内,则P点的坐标为 .
A.(3,-4) B.(-3,4) C.4,-3) D.(-4,3)
3.过点P(1,-2)作x轴的平行线l,过点Q(-4,3)作y轴的平行线l, l、l 相交于点A,则点A的坐标是
1 2 1 2
.
A.(1,3) B.(-4,-2) C.(3,1) D.(-2,-4)
知识点25:基本函数图像与性质
1.若点A(-1,y )、B(- ,y)、C( ,y)在反比例函数y= (k<0)的图象上,则下列各式中不正确的是 .
1 2 3
A.y 2 B.m<2 C.m<0 D.m>0
3.已知:如图,过原点O的直线交反比例函数y= 的图象于A、B两点,AC⊥x轴,AD⊥y轴,△ABC的面
积为S,则 .
A.S=2 B.24
4.已知点(x,y)、(x,y)在反比例函数y=- 的图象上, 下列的说法中:
1 1 2 2
①图象在第二、四象限;②y随x的增大而增大;③当01 B. k<1 C. 00;②2a+b<0;③a> ;④c<1.其中正确的
(2,1)
结论是 . O 1 x
A.①②③ B.①③④
C.①②④ D.②③④
2. 已知:如图,抛物线y=ax2+bx+c的图象如图所示,则下列结论:①abc>0; ② ;
y
③a> ; ④b>1.其中正确的结论是 .
2
A.①② B.②③ C.③④ D.②④
-1 O 1
x
y
3. 已知:如图所示,抛物线y=ax2+bx+c的对称轴为x=-1,则下列结论正确的个
数是 .
①abc>0 ②a+b+c>0 ③c>a ④2c>b
A.①②③④ B.①③④ C.①②④ D.①②③ x
-1 O
4. 已知二次函数y=ax2+bx+c的图象与x轴交于点(-2,0),(x,0),且10.其中正确结论的个数为 .
A1个 B2个 C3个 D4个
y
5. 已知:如图所示,抛物线y=ax2+bx+c的对称轴为x=-1,且过点(1,-2),则下列结论正确的个数
x
-1 O
(1,-2)是 .
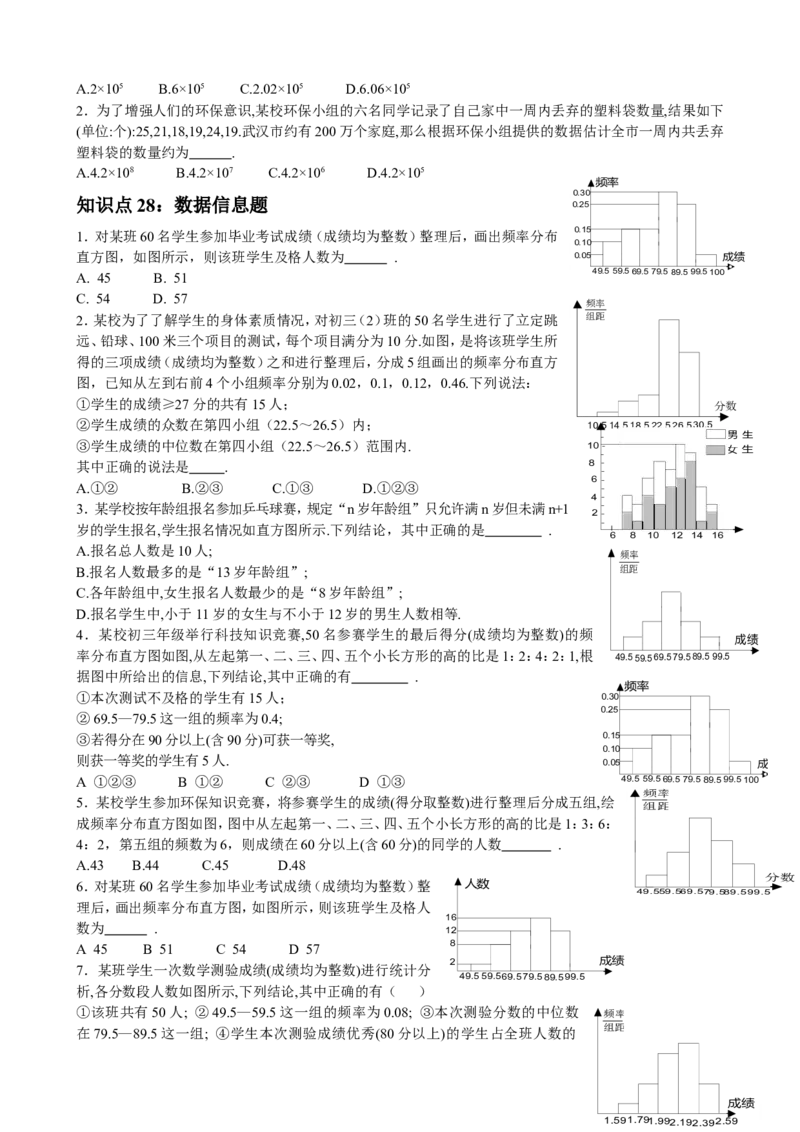
①abc>0 ② >-1 ③b<-1 ④5a-2b<0
A.①②③④ B.①③④ C.①②④ D.①②③
y
6. 已知:如图所示,抛物线y=ax2+bx+c的图象如图所示,下列结论:①a<-1;②-1b>c B.a>c>b
C.a>b=c D.a、b、c的大小关系不能确定 x
-1 O
y
8. 如图,抛物线y=ax2+bx+c图象与x轴交于A(x ,0)、B(x ,0)两点,则下列结论
1 2
2
中: ①2a+b<0; ②a<-1;③a+b+c>0; ④0-1 ③02a+ ;④3a+c<0.其中正确的个数是 .
A
A.1个 B. 2个 C.3个 D.4个 x
D
-
┙
1
┙1
2
┙
3
┙
知识点35:多项选择问题 E
B · C
1.已知:如图,△ABC中,∠A=60º,BC为定长,以BC为直径的⊙ O
2.O分别交AB、AC于点D、E,连结DE、OE.下列结论:
①BC=2DE;②D点到OE的距离不变;③BD+CE=2DE;④OE为 △ADE 外接
圆的切线.其中正确的结论是 .
A
A.①② B.③④ C.①②③ D.①②④
F
E
2.已知:如图,⊙O是△ABC的外接圆,AD⊥BC,CE⊥AB ,D、E分别为垂足,AD交CE于 O
•
H
H点,交⊙O于N,OM⊥BC,M为垂足,BO延长交⊙O于F点,下列结论:其中正确的有
B M D C
.
N
①∠BAO=∠CAH; ②DN=DH;
③四边形AHCF为平行四边形;④CH•EH=OM•HN.
A.①②③ B.②③④ C.①③④ D.①②③④
E
A
3.已知:如图,P为⊙O外一点,PA、PB切⊙O于A、B两点,OP交⊙O于点C,连结BO交延长 D
分别交⊙O及切线PA于D、E两点,连结AD、BC.下列结论:①AD∥PO;②ΔADE∽ΔPCB;
• P
O C
③tan∠EAD= ;④BD2=2AD•OP.其中正确的有 .
B
A.①②④ B.③④ C.①③④ D.①④
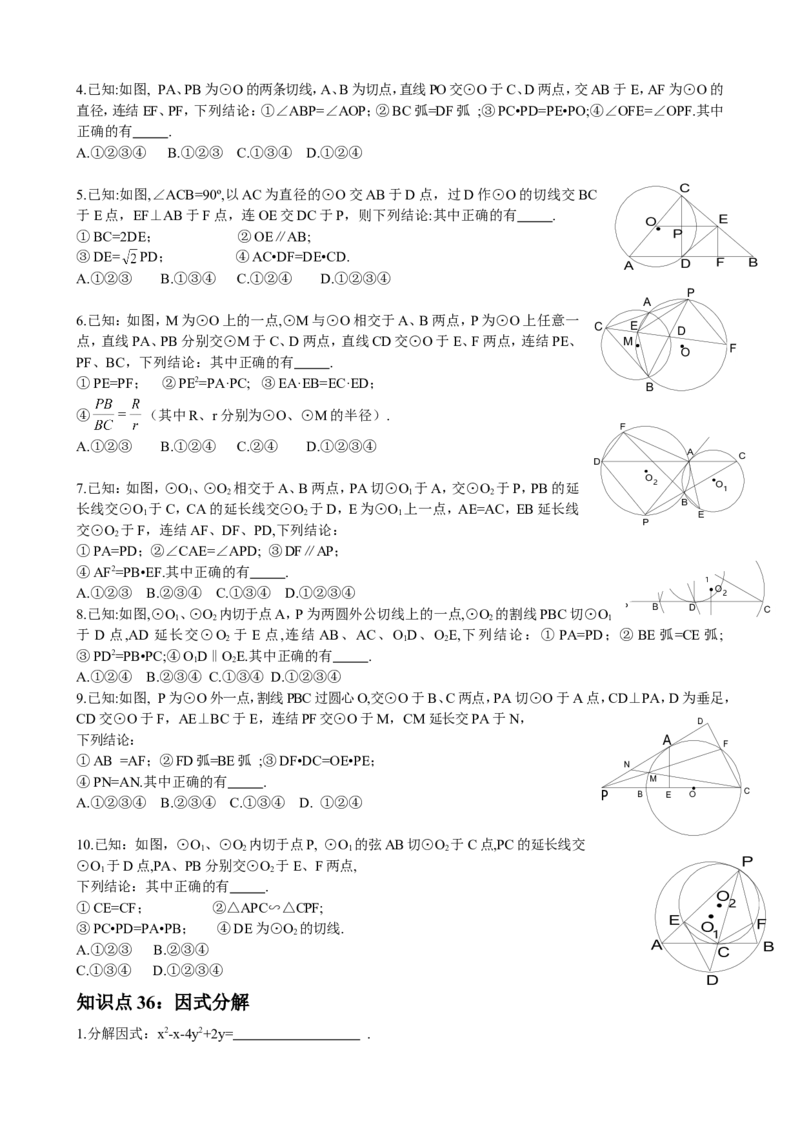
A
C E • O D
P
B F4.已知:如图, PA、PB为⊙O的两条切线,A、B为切点,直线PO交⊙O于C、D两点,交AB于E,AF为⊙O的
直径,连结EF、PF,下列结论:①∠ABP=∠AOP;②BC弧=DF弧 ;③PC•PD=PE•PO;④∠OFE=∠OPF.其中
正确的有 .
A.①②③④ B.①②③ C.①③④ D.①②④
5.已知:如图,∠ACB=90º,以AC为直径的⊙O交AB于D点,过D作⊙O的切线交BC C
于E点,EF⊥AB于F点,连OE交DC于P,则下列结论:其中正确的有 .
O E
•
①BC=2DE; ②OE∥AB; P
③DE= PD; ④AC•DF=DE•CD.
A D F B
A.①②③ B.①③④ C.①②④ D.①②③④
P
A
6.已知:如图,M为⊙O上的一点,⊙M与⊙O相交于A、B两点,P为⊙O上任意一
C E
D
点,直线PA、PB分别交⊙M于C、D两点,直线CD交⊙O于E、F两点,连结PE、 M· · O F
PF、BC,下列结论:其中正确的有 .
①PE=PF; ②PE2=PA·PC; ③EA·EB=EC·ED;
B
④ (其中R、r分别为⊙O、⊙M的半径).
F
A.①②③ B.①②④ C.②④ D.①②③④
A C
D
•
7.已知:如图,⊙O、⊙O 相交于A、B两点,PA切⊙O 于A,交⊙O 于P,PB的延
O
2
•
O
1 2 1 2 1
长线交⊙O 于C,CA的延长线交⊙O 于D,E为⊙O 上一点,AE=AC,EB延长线 B
1 2 1 E
P
交⊙O 于F,连结AF、DF、PD,下列结论:
2
A
①PA=PD;②∠CAE=∠APD; ③DF∥AP;
④AF2=PB•EF.其中正确的有 . •O
1
A.①②③ B.②③④ C.①③④ D.①②③④ •O
2
8.已知:如图,⊙O、⊙O 内切于点A,P为两圆外公切线上的一点,⊙O 的割线PBC切⊙O P B D C
1 2 2 1
于 D 点,AD 延长交⊙O 于 E 点,连结 AB、AC、OD、OE,下列结论:① PA=PD;② BE 弧=CE 弧;
2 1 2
③PD2=PB•PC;④OD‖OE.其中正确的有 . E
1 2
A.①②④ B.②③④ C.①③④ D.①②③④
9.已知:如图, P为⊙O外一点,割线PBC过圆心O,交⊙O于B、C两点,PA切⊙O于A点,CD⊥PA,D为垂足,
CD交⊙O于F,AE⊥BC于E,连结PF交⊙O于M,CM延长交PA于N,
D
下列结论: A
F
①AB =AF;②FD弧=BE弧 ;③DF•DC=OE•PE;
N
④PN=AN.其中正确的有 . M
A.①②③④ B.②③④ C.①③④ D. ①②④
P B E O
•
C
10.已知:如图,⊙O、⊙O 内切于点P, ⊙O 的弦AB切⊙O 于C点,PC的延长线交
1 2 1 2
⊙O 于D点,PA、PB分别交⊙O 于E、F两点, P
1 2
下列结论:其中正确的有 .
O
①CE=CF; ②△APC∽△CPF; • 2
E
•
③PC•PD=PA•PB; ④DE为⊙O 的切线. O F
2 1
A.①②③ B.②③④ A C B
C.①③④ D.①②③④
D
知识点36:因式分解
1.分解因式:x2-x-4y2+2y= .2.分解因式:x3-xy2+2xy-x= .
3.分解因式:x2-bx-a2+ab= .
4.分解因式:x2-4y2-3x+6y= .
5.分解因式:-x3-2x2-x+4xy2= .
6.分解因式:9a2-4b2-6a+1= .
7.分解因式:x2-ax-y2+ay= .
8.分解因式:x3-y3-x2y+xy2= .
9.分解因式:4a2-b2-4a+1= .
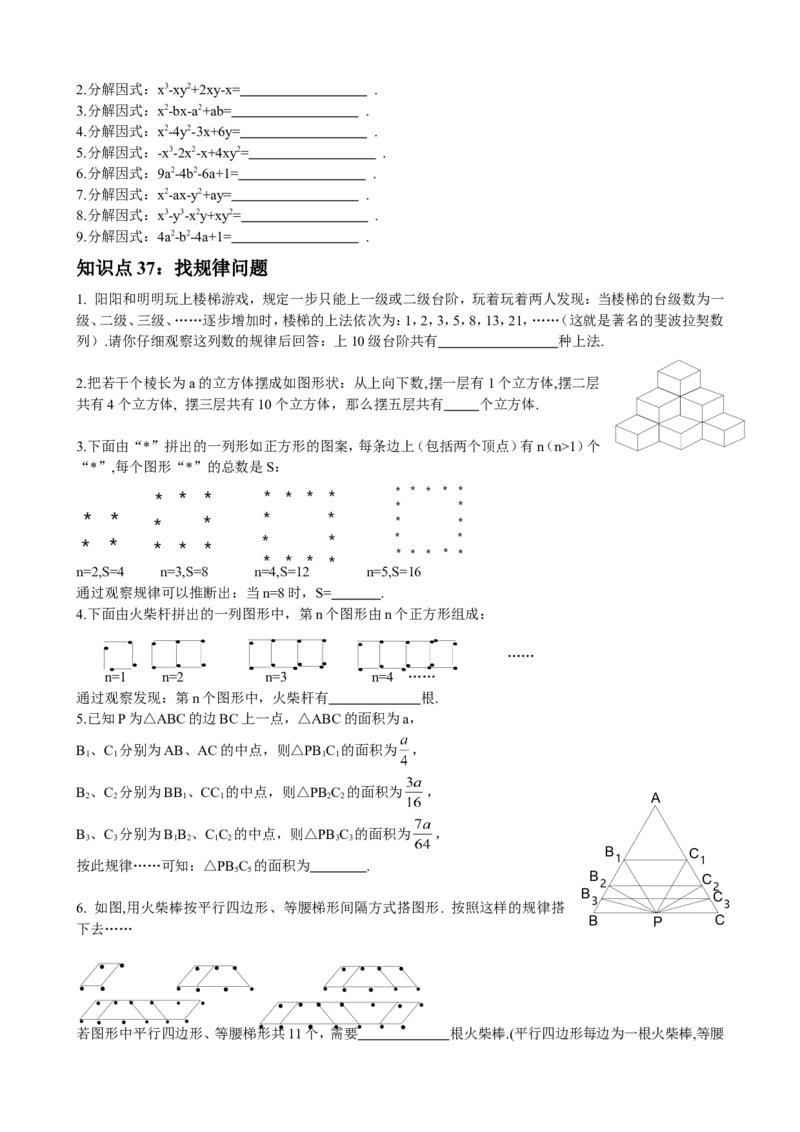
知识点37:找规律问题
1. 阳阳和明明玩上楼梯游戏,规定一步只能上一级或二级台阶,玩着玩着两人发现:当楼梯的台级数为一
级、二级、三级、……逐步增加时,楼梯的上法依次为:1,2,3,5,8,13,21,……(这就是著名的斐波拉契数
列).请你仔细观察这列数的规律后回答:上10级台阶共有 种上法.
2.把若干个棱长为a的立方体摆成如图形状:从上向下数,摆一层有1个立方体,摆二层
共有4个立方体, 摆三层共有10个立方体,那么摆五层共有 个立方体.
3.下面由“*”拼出的一列形如正方形的图案,每条边上(包括两个顶点)有n(n>1)个
“*”,每个图形“*”的总数是S:
* * * * * * * * * * * *
* *
* * * * * * * *
* * * * * * * *
* * * *
*
*
* * * *
n=2,S=4 n=3,S=8 n=4,S=12 n=5,S=16
通过观察规律可以推断出:当n=8时,S= .
4.下面由火柴杆拼出的一列图形中,第n个图形由n个正方形组成:
• • • • • • • • • • • • •• •
……
n
•
= 1
• •
n=
•
2
• •
n
•
= 3
• • •• •
n=
•
4
• •
… …
•• •
通过观察发现:第n个图形中,火柴杆有 根.
5.已知P为△ABC的边BC上一点,△ABC的面积为a,
B 、C 分别为AB、AC的中点,则△PB C 的面积为 ,
1 1 1 1
B 、C 分别为BB 、CC 的中点,则△PB C 的面积为 ,
2 2 1 1 2 2 A
B 、C 分别为B B 、C C 的中点,则△PB C 的面积为 ,
3 3 1 2 1 2 3 3
B C
按此规律……可知:△PB C 的面积为 . 1 1
5 5
B C
2 2
B C
6. 如图,用火柴棒按平行四边形、等腰梯形间隔方式搭图形. 按照这样的规律搭 3 3
B P C
下去… …
• • • • • • • • •
• • • • • • • • • • •
• • • • • • • • • • • • •
• • • • • • • • • • • • •
若图形中平行四边形、等腰梯形共11个,需要 根火柴棒.(平行四边形每边为一根火柴棒,等腰梯形上底,两腰为一根火柴棒,下底为两根火柴棒)
7.如图的三角形数组是我国古代数学家杨辉发现的,
称为杨辉三角形.根据图中的数构成的规律可得: 1 3 3 1
1 4 a 4 1
图中a所表示的数是 . 1 5 10 10 5 1
8. 在同一平面内:两条直线相交有 个交点,三条直线两两相交最多有 个交点,四条直线
两两相交最多有 个交点,……
那么8条直线两两相交最多有 个交点.
A
9.观察下列等式:13+23=32;13+23+33=62;13+23+33+43=102……; F
E · O
根据前面各式规律可得:13+23+33+43+53+63+73+83= .
知识点38:已知结论寻求条件问题 P B D C
C
1. 如图, AC为⊙O的直径,PA是⊙O的切线,切点为A,PBC是⊙O的割线,∠BAC
的平分线交BC于D点,PF交AC于F点,交AB于E点,要使AE=AF,则PF应满足的 A O • B P
条件是 . (只需填一个条件)
A
D
2.已知:如图,AB为⊙O的直径,P为AB延长线上的一点,PC切⊙O于C,要使得AC=PC, P
B
则图中的线段应满足的条件是 . •
O
3.已知:如图,四边形ABCD内接于⊙O,过A作⊙O的切线交CB的延长线于P,若它的边满
C
足条件 ,则有ΔABP∽ΔCDA.
D C
4.已知: ΔABC中,D为BC上的一点,过A点的⊙O切BC于D点,交AB、AC于 G
F
E、F两点,要使BC‖EF,
则AD必满足条件 . A E · O B
5.已知:如图,AB为⊙O的直径,D为弧AC上一点,DE⊥AB于E,DE、DB分别交
弦 AC 于 F 、 G 两 点 , 要 使 得 DE=DG , 则 图 中 的 弧 必 满 足 的 条 件 是 C
D
.
E
6.已知:如图,Rt△ABC中,以AB为直径作⊙O交BC 于D点,E为AC上一点,要使得 A O • B
AE=CE,请补充条件
(填入一个即可).
7.已知:如图,圆内接四边形ABCD,对角线ACBD相交于E点,要使得BC2=CE•CA,则四边形
D
ABCD的边应满足的条件是 .
A O •
E
C
8.已知,ΔABC内接于⊙O,要使∠BAC的外角平分线与⊙O相切,则ΔABC的边必满足的条件
B
是 . A
9.已知: 如图,ΔABC内接于⊙O,D为劣弧AB上一点,E是BC延长线上一点,AE交⊙O D O F
•
于F,为使ΔADB∽ΔACE,应补充的一个条件是 ,或 .
B C E10.已知:如图,以△ABC的边AB为直径作⊙O交BC于D,DE⊥AC,E为垂足,要使得
DE 为 ⊙ O 的切线,则 △ ABC 的 边 必 满 足 的 条 件 是
.
知识点39:阴影部分面积问题
1. 如图,梯形ABCD中,AD∥BC,∠D=90°,以AB为直径的⊙
O切CD于E点,交BC于F,若AB=4cm,AD=1cm, 则图中阴影部分的面积是 cm2(. 不用近似值)
2.已知:如图,平行四边形 ABCD,AB⊥AC,AE⊥BC,以AE为直径作
A G
⊙O,以A为圆心,AE为半径作弧交 AB于F点,交AD于G点,若 D
BE=2,CE=6,则图中阴
•O
影部分的面积为 .
F
B
E C
3.已知:如图, ⊙O 与⊙O 内含,直线OO 分别交⊙O 和⊙O 于A、B和
1 2 1 2 1 2
C、D点,⊙O 的弦BE切⊙O 于F点,若AC=1cm,CD=6cm,DB=3cm,则弧CF、AE与线
1 2
段AC弧、EF弧围成的阴影部分的面积
是 cm2. M C D N A C O • 2 O •1 D B
4.已知:如图,AB为⊙O 的直径,以AO、BO为直径作⊙O 、⊙O , A O • O O • B F
1 2 1 2
⊙O的弦 MN与⊙O、⊙O 相切于C、D两点,AB=4,则图中阴影部 E
1 2
分的面积是 .
5.已知:如图,等边△ABC内接于⊙O,以AB为直径作⊙O,AB=2 ,则图中阴影
1 2
部分的面积为 .
6.已知:如图,边长为12的等边三角形,形内有4个等圆,则图中阴影部分的面积为
.
7.已知:如图,直角梯形ABCD中,AD∥BC,AD=AB=2 ,BC=4,∠A=90°,以A为
圆心,AB为半径作扇形ABD,以BC为直径作半圆,则图中阴影部分的面积为 .
A D
8.已知:如图, ABCD,AB⊥AC,AE⊥BC,以AE为直径作⊙O,以A为圆心,AE为半
径作弧交AB于F点,交AD于G点,若BE=6,CE=2,则图中阴影部分的面积为
•
.
B C
A G D
F
O
B E C
B D
9.已知:如图,⊙O 的半径为1cm,AO交⊙O于C,AO=2cm,AB与⊙O相切于B点,弦
•
CD‖AB,则图中阴影部分的面积是 . A C O
B
10.已知:如图,以⊙O的半径OA为直径作⊙O,OB⊥OA交⊙O于B,OB交⊙O 于
1 1 1
C
• •
A O1 OC,OA=4,则图中阴影部分的面积为 .