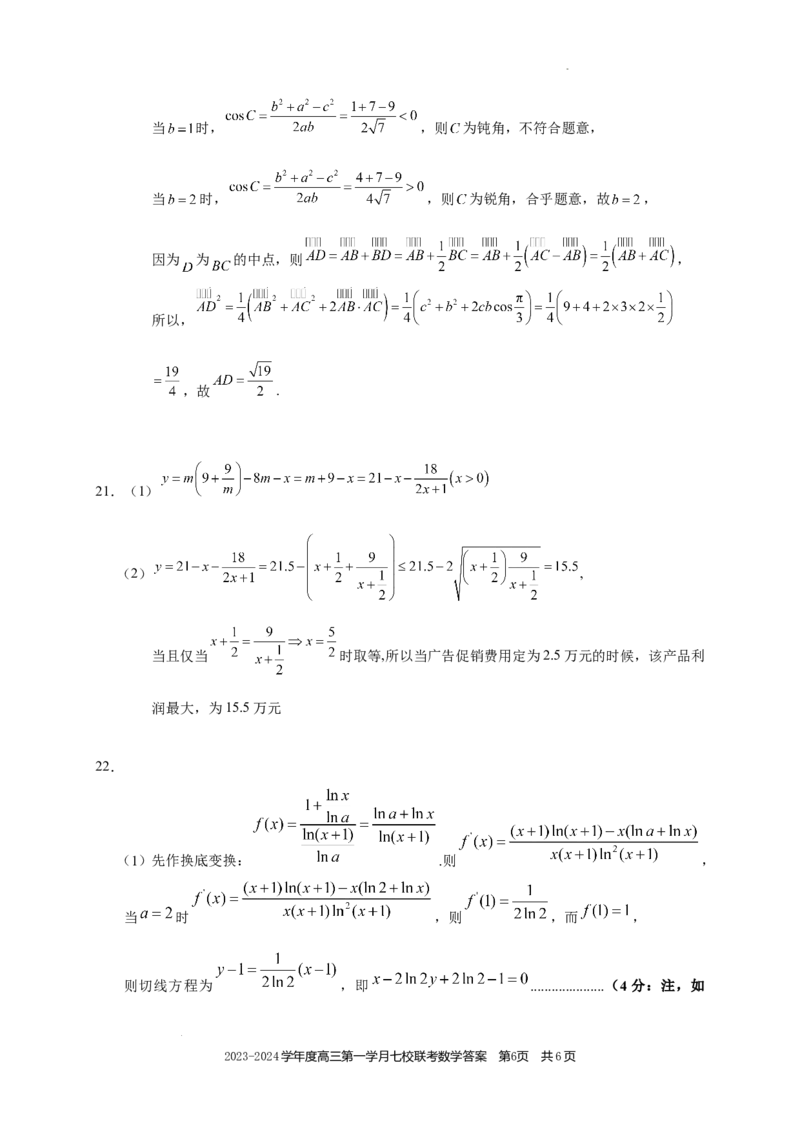文档内容
2023—2024 学年度高三第一学月七校联考
高三数学答案
1 2 3 4 5 6 7 8 9 10 11 12
B D A C C A B A BC BCD ACD ABD
13. 7 14. 15. 16. 12 3
8.【详解】正数 满足 ,
所以 ,即 ,所以 ,
令 ,所以 在 上单调递增,
所以 ,即 ,
所以 ,令 ,
所以 在 上 单减;在 上 单增,
所以 的最小值是 ,所以 的最小值为 .
选A
12.【详解】函数 ,
求导得 ,再次求导得 ,
对于A,当 时, ,有 ,函数 在
上单调递增,A正确;
对于 B,当 时, ,有 ,函数 在
2023-2024学年度高三第一学月七校联考数学答案 第1页 共6页
学科网(北京)股份有限公司上单调递增,
而 ,则 使得 ,
当 时, ,当 时, ,因此 在 上递减,在
上递增,
由 选 项 A 知 , 在 上 递 增 , 又
,则 ,
使得 ,因此函数 在 上有两个零点,B正确;
对于C,对 恒有 ,由选项B知, ,
则有 ,由 得: ,
,
令 , ,
函数 在 上单调递减, ,又 ,
则有 ,因此整数 的最大值为 ,C不正确;
对 于 D , 当 时 , 令 , 则
,
函数 在 上递减, ,即 ,函数 在 上递增,
,即 ,
令 , ,
显然 在 上单调递增,则有函数 在 上单调递增,
2023-2024学年度高三第一学月七校联考数学答案 第2页 共6页
学科网(北京)股份有限公司因此 ,即 ,所以当 时, 成立,D正确.
故选:ABD
16.【详解】由 可得 ,由 ,则 ,则
. 因 为 , 所 以 , 则
,则 ,
,
则 ,则 .因为 ,则
,则 ,当且仅
当 ,即 时取得等号.故 ,面积最大值为 .
解答题
17.(1) , ,
, ,
或 ,
(2)无论选①还是选②还是选③,均等价于 ,
①若 ,则 ,解得 ,
②若 ,则 ,解得 ,
综上,
2023-2024学年度高三第一学月七校联考数学答案 第3页 共6页
学科网(北京)股份有限公司18.
(1)∵
∴ 的最小正周期 ,
由 , ,解得 , ,
的单调递增区间为 , ;
(2) ,
, ,则 , ,
19.(1)由题设 ,则 ,
所以在 上 , 递增,在 上 , 递减,
则 ,极大值 ,
综上, 最大值为 ,最小值为 .
(2)(法1)根据题意,只需 即可,
2023-2024学年度高三第一学月七校联考数学答案 第4页 共6页
学科网(北京)股份有限公司一方面,由 在 上 ,
另一方面,由 且 ,
当 时, ,此时 递增且值域为R,所以满足题设;
当 时, 上 , 递增; 上 , 递减;
所以 ,此时 ,可得 ,
综上,a的取值范围 .
(法2)因为 在 上 ,
原问题等价于 使得 成立,
即 使得 成立,即
令 ,则
所以 在区间 上单减,在区间 上单增
所以 ,从而
20.(1)解:因为 ,由正弦定理可得 ,
所以, ,
因为 ,所以 ,所以 ,因为 ,所以 .
(2)解:在△ABC中,因为 ,
所以 ,所以 ,解得 或
2023-2024学年度高三第一学月七校联考数学答案 第5页 共6页
学科网(北京)股份有限公司当 时, ,则 为钝角,不符合题意,
当 时, ,则 为锐角,合乎题意,故 ,
因为 为 的中点,则 ,
所以,
,故 .
21.(1)
(2) ,
当且仅当 时取等,所以当广告促销费用定为2.5万元的时候,该产品利
润最大,为15.5万元
22.
(1)先作换底变换: .则 ,
当 时 ,则 ,而 ,
则切线方程为 ,即 .....................(4分:注,如
2023-2024学年度高三第一学月七校联考数学答案 第6页 共6页
学科网(北京)股份有限公司果没作换底求对了也给分,导数求对给1分,斜率算对1分,函数值求对给1分,方程求对给1
分)
(2)由(1)知 ,分母不影响符号,故只研究分
子 的 变 化 情 况 . 设 , 则
. ..............(1分)
第一种情形,若 ,则 ,而 ,则 在 上恒成立,则
在 上单调递增,又因为当 时, ,则 在 上恒成立,
即 在 上恒成立,则 在 上单调递增,则 在定义域内无极值点.
.....................(1分)
第二种情形,若 ,令 得 ,易知 在 单调递减,当
时, , 单调递增,当 时, , 单调递减.
而 ,又因为当 时,
, 当 时 , , 则 存 在 唯 一 的 实 数 , 使 得 当
时, , , 单调递增,当 时, , ,
2023-2024学年度高三第一学月七校联考数学答案 第7页 共6页
学科网(北京)股份有限公司单 调 递 减 , 则 为 函 数 的 极 大 值 点 , 所 以 的 取 值 范 围 为 .
.........................(3分)
由前面的分析知 的极大值点 满足方程 ,
而 , 则 ,
当且仅当 时取等号,此时 .故 成立. ..................(3分)
(注:如果学生分离参数解决,求 的范围正确给3分,证明不等式正确给5分,具体细则自
行决定,其他情况请酌情给分。)
2023-2024学年度高三第一学月七校联考数学答案 第8页 共6页
学科网(北京)股份有限公司