专题08平面解析几何（解答题）（解析版）_赠送：2008-2024全套高考真题_高考数学真题_送高考数学五年真题(2019-2023)分项汇编（全国通用）

五年（2019-2023）年高考真题分项汇编 专题 08 平面解析几何（解答题） 平面解析几何在高考中考查比例较大，一般是1+1+1模式或者是2+1+1模式。在选题中，解析几何解答题 中难度一般较大，计算量比较大.主要知识点是 考点01 椭圆及其性质 考点02 双曲线及其性质 考点03 抛物线及其性质 考点 01 椭圆及其性质 1.(2020年新高考全国卷Ⅱ数学(海南)·第21题)已知椭圆C： 过点M(2，3),点A 为其左顶点，且AM的斜率为 ， (1)求C的方程； (2)点N为椭圆上任意一点，求△AMN的面积的最大值． 【答案】(1) ；(2)18． 解析：(1)由题意可知直线AM的方程为： ，即 ． 当y=0时，解得 ，所以a=4， 椭圆 过点M(2，3)，可得 ， 解得b2=12． 所以C的方程： ． (2)设与直线AM平行的直线方程为： ， 如图所示，当直线与椭圆相切时，与AM距离比较远的直线与椭圆的切点为N，此时△AMN的面积取 得最大值． 1联立直线方程 与椭圆方程 ， 可得： ， 化简可得： ， 所以 ，即m2=64，解得m=±8， 与AM距离比较远的直线方程： ， 直线AM方程为： ， 点N到直线AM的距离即两平行线之间的距离， 利用平行线之间的距离公式可得： ， 由两点之间距离公式可得 ． 所以△AMN的面积的最大值： ． 2.(2020江苏高考·第18题)在平面直角坐标系 中，已知椭圆 的左、右焦点分别为 ，点 在椭圆 上且在第一象限内， ，直线 与椭圆 相交于另一点 ． 2(1)求 的周长； (2)在 轴上任取一点 ，直线 与椭圆 的右准线相交于点 ，求 的最小值； (3)设点 在椭圆 上，记 与 的面积分别为 ，若 ，求点 的坐标． 【答案】【答案】(1) ；(2) ；(3) 或 ． 【解析】(1)∵椭圆 的方程为 , , 由椭圆定义可得： ． 的周长为 (2)设 ，根据题意可得 ．∵点 在椭圆 上，且在第一象限， ,∵准线方程为 , , ，当且仅当 时取等号． 的最小值为 ． (3)设 ，点 到直线 的距离为 ． ， ∴直线 的方程为 ,∵点 到直线 的距离为 ， , , ① ②,∴联立①②解得 ， ． 或 ． 33.(2020年高考课标Ⅲ卷理科·第20题)已知椭圆 的离心率为 ， ， 分别 为 的左、右顶点． (1)求 的方程； (2)若点 在 上，点 在直线 上，且 ， ，求 的面积． 【答案】(1) ；(2) ． 解析：(1) ， ， 根据离心率 ， 解得 或 (舍)， 的方程为： ， 即 ； (2)不妨设 , 在x轴上方 点 在 上，点 在直线 上，且 ， ， 过点 作 轴垂线，交点为 ，设 与 轴交点为 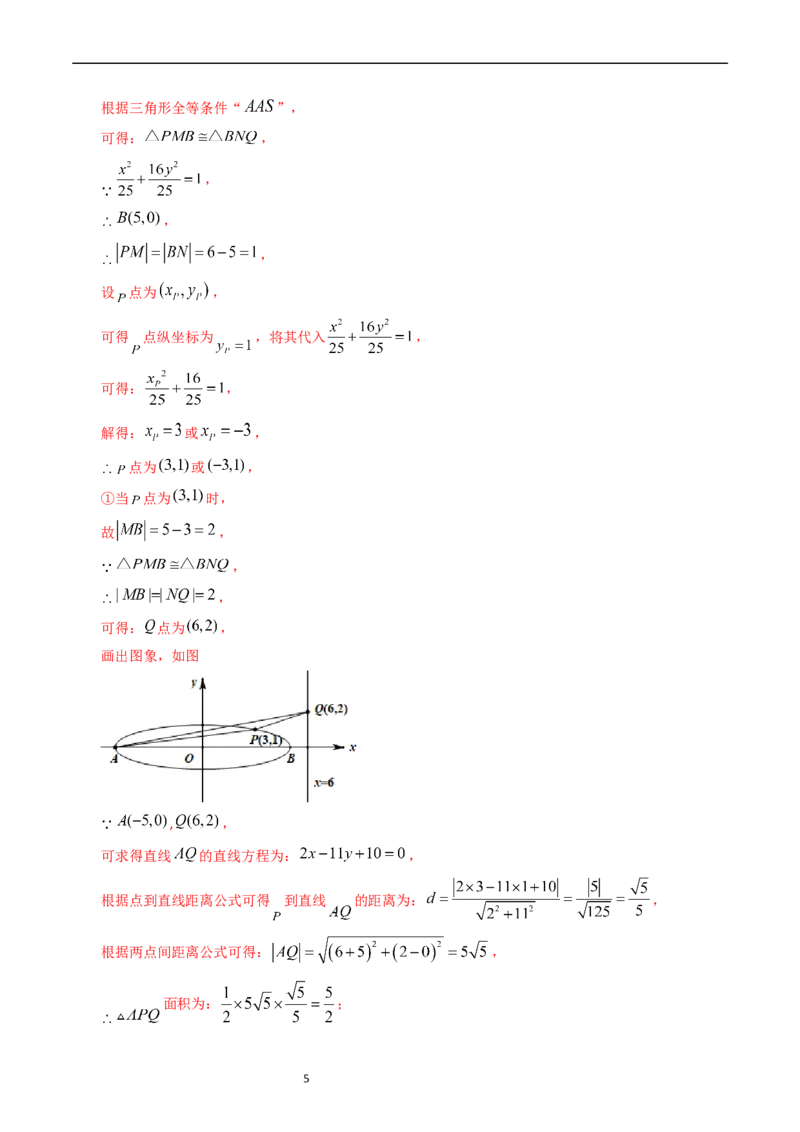根据题意画出图形，如图 ， ， ， 又 ， ， ， 4根据三角形全等条件“ ”， 可得： ， ， ， ， 设 点为 ， 可得 点纵坐标为 ，将其代入 ， 可得： ， 解得： 或 ， 点为 或 ， ①当 点为 时， 故 ， ， ， 可得： 点为 ， 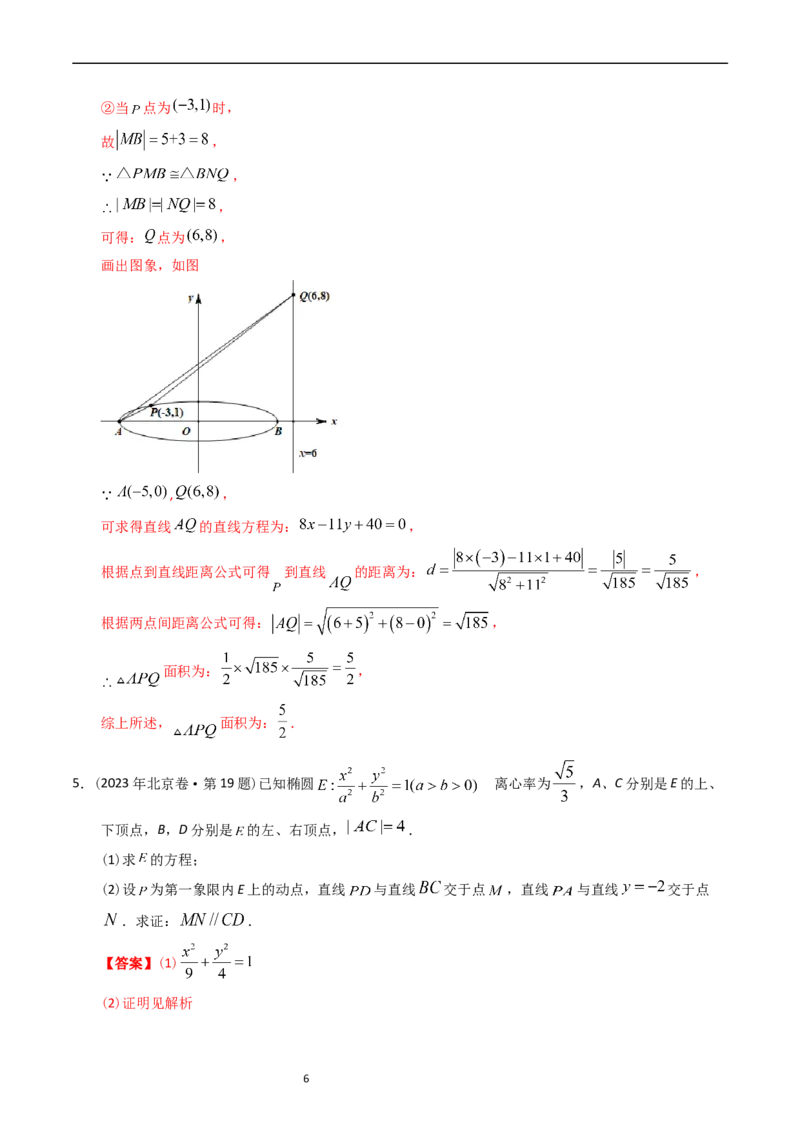画出图象，如图 , ， 可求得直线 的直线方程为： ， 根据点到直线距离公式可得 到直线 的距离为： ， 根据两点间距离公式可得： ， 面积为： ； 5②当 点为 时， 故 ， ， ， 可得： 点为 ， 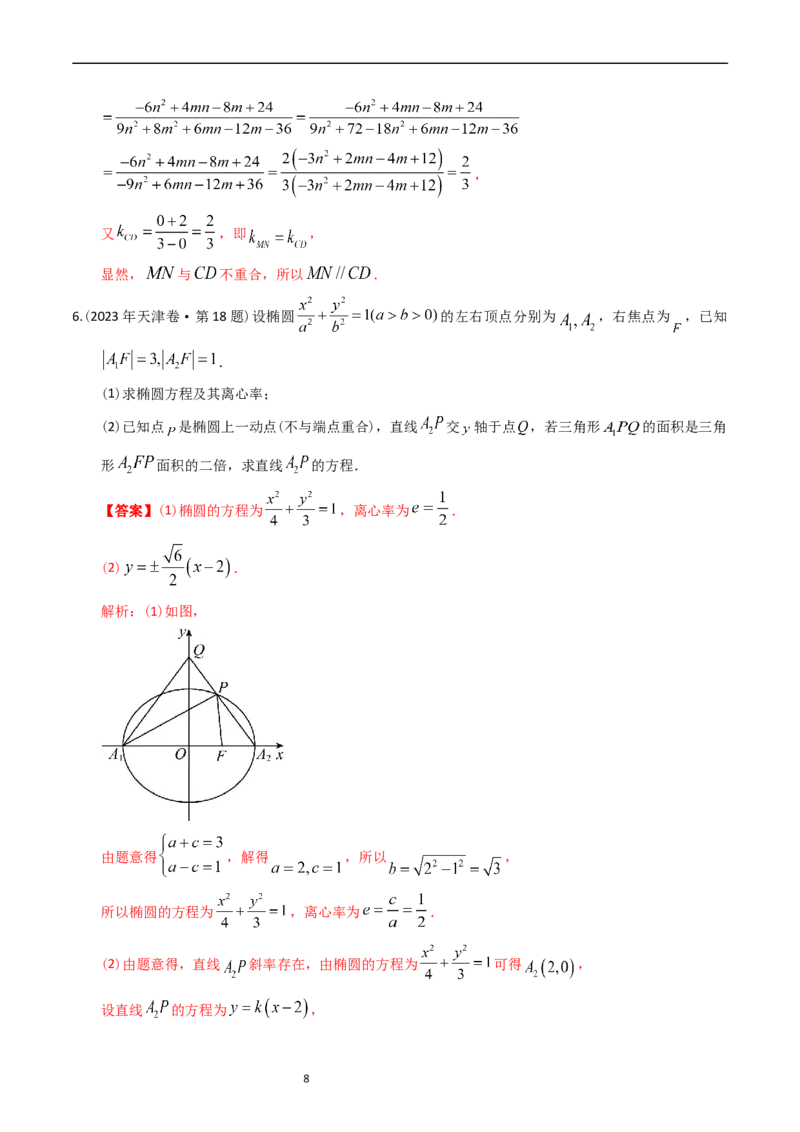画出图象，如图 , ， 可求得直线 的直线方程为： ， 根据点到直线距离公式可得 到直线 的距离为： ， 根据两点间距离公式可得： ， 面积为： ， 综上所述， 面积为： ． 5．(2023年北京卷·第19题)已知椭圆 离心率为 ，A、C分别是E的上、 的 下顶点，B，D分别是 的左、右顶点， ． (1)求 的方程； (2)设 为第一象限内E上的动点，直线 与直线 交于点 ，直线 与直线 交于点 ．求证： ． 【答案】(1) (2)证明见解析 6解析：(1)依题意，得 ，则 ， 又 分别为椭圆上下顶点， ，所以 ，即 ， 所以 ，即 ，则 ， 所以椭圆 的方程为 ． (2)因为椭圆 的方程为 ，所以 ， 因为 为第一象限 上的动点，设 ，则 ， 易得 ，则直线 的方程为 ， ，则直线 的方程为 ， 联立 ，解得 ，即 ， 而 ，则直线 的方程为 ， 令 ，则 ，解得 ，即 ， 又 ，则 ， ， 所以 7， 又 ，即 ， 显然， 与 不重合，所以 ． 6.(2023年天津卷·第18题)设椭圆 的左右顶点分别为 ，右焦点为 ，已知 ． (1)求椭圆方程及其离心率； (2)已知点 是椭圆上一动点(不与端点重合)，直线 交 轴于点 ，若三角形 的面积是三角 形 面积的二倍，求直线 的方程． 【答案】(1)椭圆的方程为 ，离心率为 ． (2) ． 解析：(1)如图， 由题意得 ，解得 ，所以 ， 所以椭圆的方程为 ，离心率为 ． (2)由题意得，直线 斜率存在，由椭圆的方程为 可得 ， 设直线 的方程为 ， 8联立方程组 ，消去 整理得： ， 由韦达定理得 ，所以 ， 所以 ， ． 所以 , , ， 所以 ， 所以 ，即 ， 解得 ，所以直线 的方程为 ． 7.(2022高考北京卷·第19题)已知椭圆： 的一个顶点为 ，焦距为 ． (1)求椭圆E的方程； (2)过点 作斜率为k的直线与椭圆E交于不同的两点B，C，直线AB，AC分别与x轴交于点M， N，当 时，求k的值． 【答案】解析:(1)依题意可得 ， ，又 ， 所以 ，所以椭圆方程为 ； (2)解：依题意过点 的直线为 ，设 、 ，不妨令 ， 由 ，消去 整理得 ， 所以 ，解得 ， 所以 ， ， 9直线 的方程为 ，令 ，解得 ， 直线 的方程为 ，令 ，解得 ， 所以 ， 所以 ， 即 即 即 整理得 ，解得 8.(2022年浙江省高考数学试题·第21题)如图，已知椭圆 ．设A，B是椭圆上异于 的两 点，且点 在线段 上，直线 分别交直线 于C，D两点． 10(1)求点P到椭圆上点的距离的最大值； (2)求 的最小值． 【答案】解析:(1)设 是椭圆上任意一点, ,则 ，当且 仅当 时取等号，故 的最大值是 ． (2)设直线 ,直线 方程与椭圆 联立,可得 , 设 ，所以 ，因为直线 与直线 交于 ,则 ,同理可得, ． 则 ， 11当且仅当 时取等号，故 的最小值为 ． 9 .(2021高考北京·第20题)已知椭圆 一个顶 点 ，以椭圆 的四个顶 点为顶点的四边形面积为 ． (1)求椭圆E的方程； (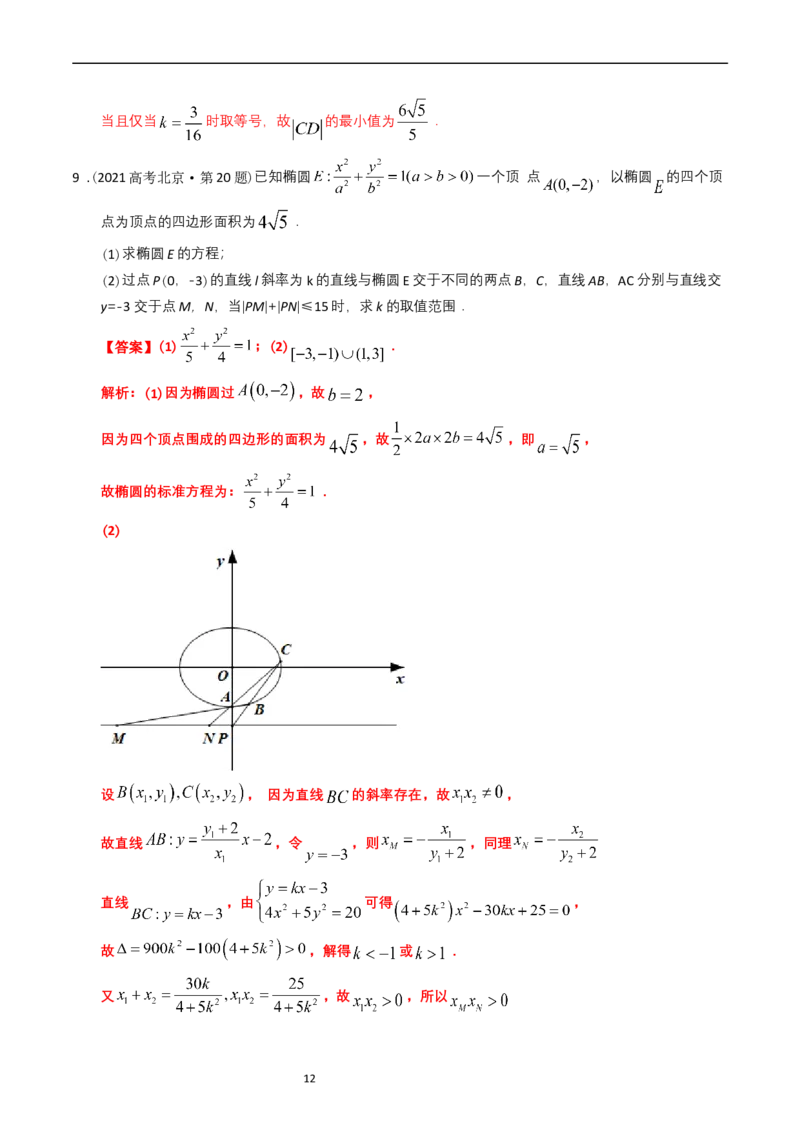2)过点P(0，-3)的直线l斜率为k的直线与椭圆E交于不同的两点B，C，直线AB，AC分别与直线交 y=-3交于点M，N，当|PM|+|PN|≤15时，求k的取值范围． 【答案】(1) ；(2) ． 解析：(1)因为椭圆过 ，故 ， 因为四个顶点围成的四边形的面积为 ，故 ，即 ， 故椭圆的标准方程为： ． (2) 设 ， 因为直线 的斜率存在，故 ， 故直线 ，令 ，则 ，同理 . 直线 ，由 可得 ， 故 ，解得 或 ． 又 ，故 ，所以 12又 故 即 ， 综上， 或 ． 10.(2020天津高考·第18题)已知椭圆 的一个顶点为 ，右焦点为 ，且 ，其中 为原点． (Ⅰ)求椭圆 的方程； (Ⅱ)已知点 满足 ，点 在椭圆上( 异于椭圆的顶点)，直线 与以 为圆心的圆相切 于点 ，且 为线段 的中点．求直线 的方程． 【答案】【答案】(Ⅰ) ；(Ⅱ) ，或 ． 【解析】(Ⅰ) 椭圆 的一个顶点为 ， ，由 ，得 ，又由 ，得 ， 所以，椭圆的方程为 ； (Ⅱ) 直线 与以 为圆心的圆相切于点 ，所以 ， 根据题意可知，直线 和直线 的斜率均存在， 设直线 的斜率为 ，则直线 的方程为 ，即 ， ，消去 ，可得 ，解得 或 ． 将 代入 ，得 ， 所以，点 的坐标为 ，因为 为线段 的中点，点 的坐标为 ， 所以点 的坐标为 ，由 ，得点 的坐标为 ， 13所以，直线 的斜率为 ，又因为 ，所以 ， 整理得 ，解得 或 ．所以，直线 的方程为 或 ． 11.(2019·上海·第20题)已知椭圆 ， 为左、右焦点，直线 过 交椭圆于A、B两点. (1)若AB垂直于 轴时，求 ； (2)当 时， 在 轴上方时，求 的坐标； (3)若直线 交 轴于M，直线 交 轴于N，是否存在直线 ，使 ，若存在，求 出直线 的方程；若不存在，请说明理由. (1) ；(2) (3) 或 【答案】 ， ； 【解析】(1)依题意： ，当AB⊥x轴，则坐标 ， ， ∴ (2)法一(秒杀)：焦点三角形面积公式： ； 又： ， ，即 所以A在短轴端点，即 直线 (即 )方程为： ，联立： ，得 . 法二(常规)：依题意：设坐标 ，∵ (注意：用点 更方便计算) 则有： 又A在椭圆上，满足： ，即： 14∴ ，解出： ， B点坐标求解方法同法一， . （2）设坐标 ， ， ， ，直线l： (k不存在时不满足题意) 则： ； ； 联立方程： ， ，韦达定理： 由直线 方程： 得M纵坐标： ； 由直线 方程： 得N纵坐标： ； 若 ，即 ∴ ， ，代入韦达定理： 得： ，解出： ∴ 存在直线 或 满足题意. 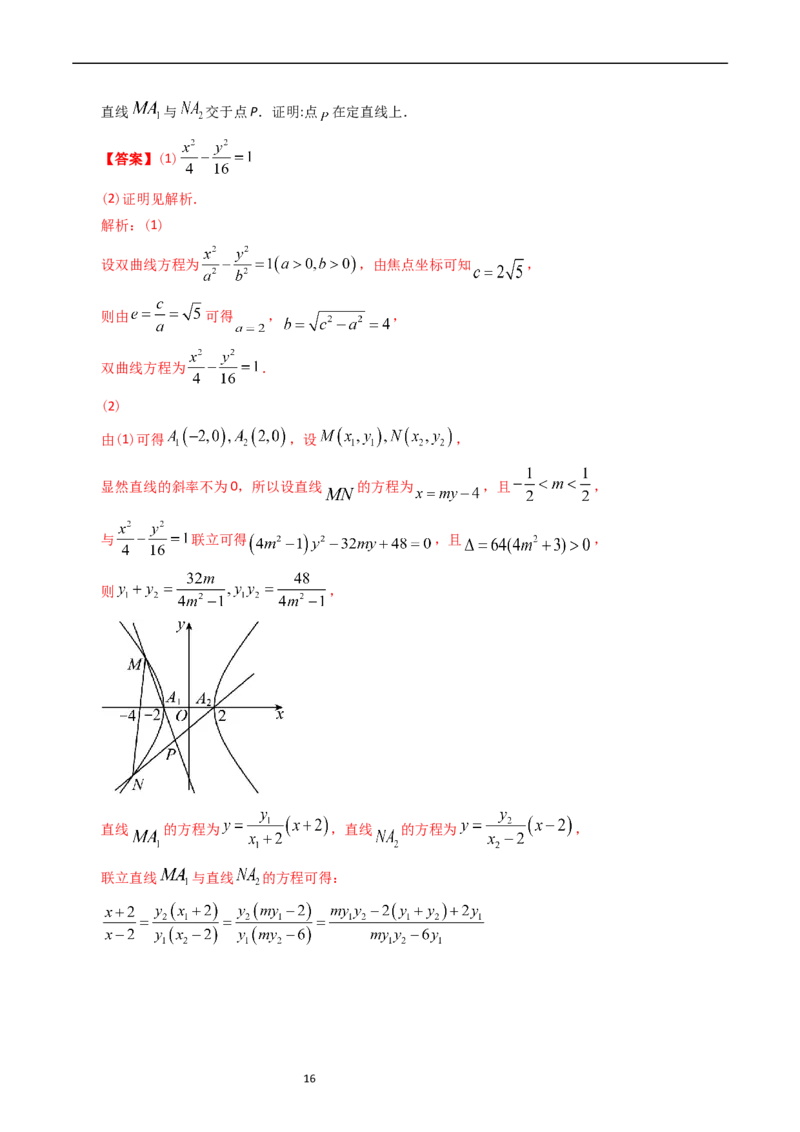考点 02 双曲线及其性质 1．(2023年新课标全国Ⅱ卷·第21题)已知双曲线C的中心为坐标原点，左焦点为 ，离心率为 ． (1)求C的方程； (2)记C 左的、右顶点分别为 ， ，过点 的直线与C的左支交于M，N两点，M在第二象限， 15直线 与 交于点P．证明:点 在定直线上． 【答案】(1) (2)证明见解析． 解析：(1) 设双曲线方程为 ，由焦点坐标可知 ， 则由 可得 ， ， 双曲线方程为 ． (2) 由(1)可得 ，设 ， 显然直线的斜率不为0，所以设直线 的方程为 ，且 ， 与 联立可得 ，且 ， 则 ， 直线 的方程为 ，直线 的方程为 ， 联立直线 与直线 的方程可得： 16， 由 可得 ，即 ， 据此可得点 在定直线 上运动． 2.(2022新高考全国II卷·第21题)已知双曲线 的右焦点为 ，渐近线方程 为 ． (1)求C的方程； (2)过F的直线与C的两条渐近线分别交于A，B两点，点 在C上，且． ．过P且斜率为 的直线与过Q且斜率为 的直线交于点M．从下面①②③中 选取两个作为条件，证明另外一个成立： ①M在 上；② ；③ ． 注：若选择不同的组合分别解答，则按第一个解答计分． 【答案】(1) (2)见解析 解析:(1)右焦点为 ，∴ ,∵渐近线方程为 ，∴ ，∴ ，∴ ，∴ ，∴ ． ∴C的方程为： ； (2)由已知得直线 的斜率存在且不为零，直线 的斜率不为零， 若选由①②推③或选由②③推①：由②成立可知直线 的斜率存在且不为零； 若选①③推②，则 为线段 的中点，假若直线 的斜率不存在，则由双曲线的对称性可知 在 轴上，即为焦点 ,此时由对称性可知 、 关于 轴对称，与从而 ，已知不符； 总之，直线 的斜率存在且不为零． 设直线 的斜率为 ,直线 方程为 , 则条件① 在 上，等价于 ； 两渐近线 的方程合并为 , 联立消去y并化简整理得： 17设 ,线段中点 ,则 , 为 设 , 则条件③ 等价于 , 移项并利用平方差公式整理得： ， ,即 , 即 ； 由题意知直线 的斜率为 , 直线 的斜率为 , ∴由 , ∴ , 所以直线 的斜率 , 直线 ,即 , 代入双曲线的方程 ,即 中， 得： , 解得 的横坐标： , 同理： ， ∴ ∴ , ∴条件② 等价于 ， 综上所述： 条件① 在 上，等价于 ； 条件② 等价于 ； 18条件③ 等价于 ； 选①②推③: 由①②解得： ,∴③成立； 选①③推②： 由①③解得： ， ， ∴ ，∴②成立； 选②③推①： 由②③解得： ， ，∴ ， ∴ ，∴①成立． 3．(2021年新高考Ⅰ卷·第21题)在平面直角坐标系 中，已知点 、 ，点 的轨迹为 ． (1)求 的方程； (2)设点 在直线 上，过 两条直线分别交 于 、 两点和 ， 两点，且 的 ，求直线 的斜率与直线 的斜率之和． 【答案】解析： 因为 ， 所以，轨迹 是以点 、 为左、右焦点的双曲线的右支， 设轨迹 的方程为 ，则 ，可得 ， ， 所以，轨迹 的方程为 ； (2)设点 ，若过点 的直线的斜率不存在，此时该直线与曲线 无公共点， 不妨直线 的方程为 ，即 ， 联立 ，消去 并整理可得 ， 19设点 、 ，则 且 ． 由韦达定理可得 ， ， 所以， ， 设直线 的斜率为 ，同理可得 ， 因为 ，即 ，整理可得 ， 即 ，显然 ，故 ． 因此，直线 与直线 的斜率之和为 ． 4.(2022新高考全国I卷·第21题)已知点 在双曲线 上，直线l交C于P，Q 两点，直线 的斜率之和为0． (1)求l 的斜率； (2)若 ，求 的面积． 【答案】(1) ； (2) ． 解析：(1)因为点 在双曲线 上，所以 ，解得 ， 即双曲线 易知直线l的斜率存在，设 ， ， 联立 可得， ， 所以， ， ． 20所以由 可得， ， 即 ， 即 ， 所以 ， 化简得， ，即 ， 所以 或 ， 当 时，直线 过点 ，与题意不符，舍去， 故 ． (2)不妨设直线 的倾斜角为 ，因为 ，所以 ， 由(1)知， ， 当 均在双曲线左支时， ，所以 ， 即 ，解得 (负值舍去) 此时PA与双曲线的渐近线平行，与双曲线左支无交点，舍去； 当 均在双曲线右支时， 因为 ，所以 ，即 ， 即 ，解得 (负值舍去)， 于是，直线 ，直线 ， 联立 可得， ， 因为方程有一个根为 ，所以 ， ， 同理可得， ， ． 所以 ， ， 21点 到直线 的距离 ， 故 的面积为 ． 考点 03 抛物线及其性质 1.(2023年全国甲卷理科·第20题)已知直线 与抛物线 交于 两点， 且 ． (1)求 ； (2)设F为C的焦点，M，N为C上两点， ，求 面积的最小值． 【答案】(1) (2) 解析：(1)设 ， 由 可得， ，所以 ， 所以 ， 即 ，因为 ，解得： ． (2)因为 ，显然直线 的斜率不可能为零， 设直线 ： ， ， 由 可得， ，所以， ， ， 因为 ，所以 ， 即 ， 亦即 ， 将 代入得， ， ， 所以 ，且 ，解得 或 ． 设点 到直线 的距离为 ，所以 ， 22， 所以 的面积 ， 而 或 ，所以， 当 时， 的面积 ． 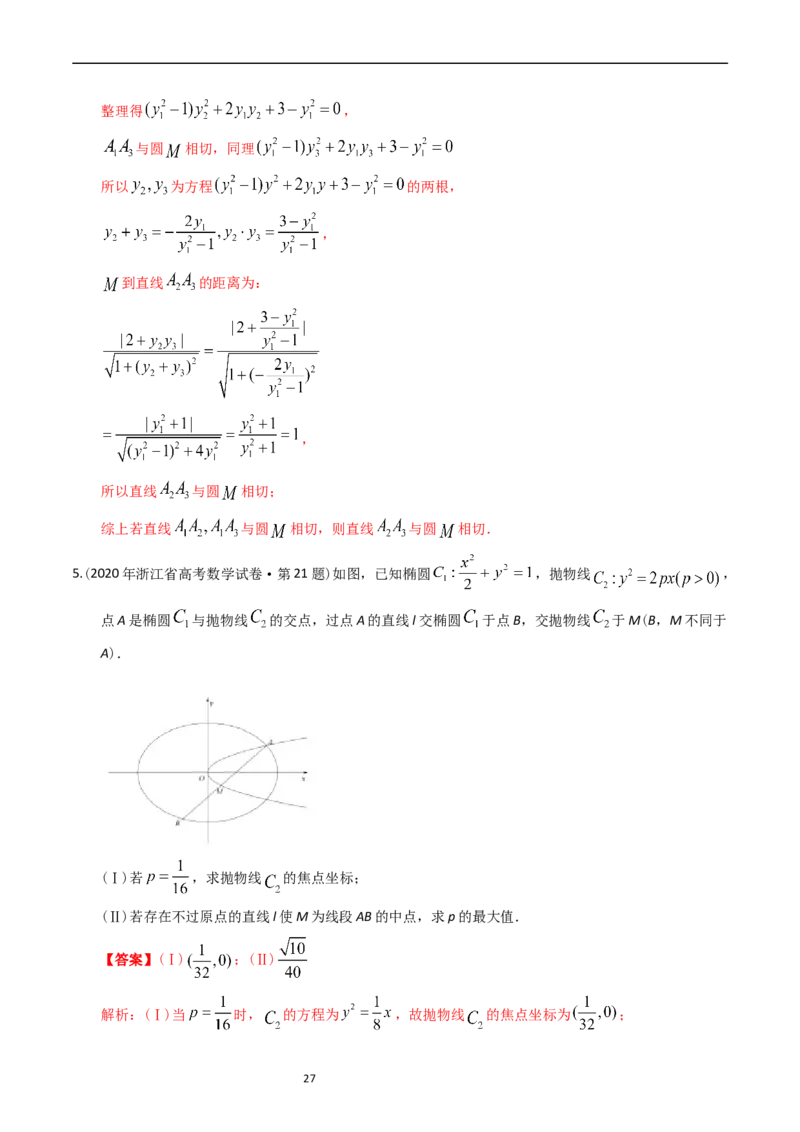2.(2021年高考浙江卷·第21题)如图，已知F是抛物线 的焦点，M是抛物线的准线与x轴 的交点，且 ， (1)求抛物线的方程； (2)设过点F的直线交抛物线与A､B两点，斜率为2的直线l与直线 ，x轴依次交于点P， Q，R，N，且 ，求直线l在x轴上截距的范围． 【答案】(1) ；(2) ． 解析:(1)因为 ，故 ，故抛物线的方程为： ． (2)设 ， ， ， 所以直线 ，由题设可得 且 ．由 可得 ，故 ， 因为 ，故 ，故 ． 23又 ，由 可得 ， 同理 ， 由 可得 ，所以 ， 整理得到 ， 故 ，令 ，则 且 ， 故 ，故 即 ， 解得 或 或 ． 故直线 在 轴上的截距的范围为 或 或 ． 3.(2021年高考全国乙卷理科·第21题)已知抛物线 的焦点为 ，且 与圆 上点的距离的最小值为 ． (1)求 ； (2)若点 在 上， 是 的两条切线， 是切点，求 面积的最大值． 【答案】(1) ；(2) ． 解析：(1)抛物线 的焦点为 ， ， 所以， 与圆 上点的距离的最小值为 ，解得 ； 24(2)抛物线 的方程为 ，即 ，对该函数求导得 ， 设点 、 、 ， 直线 的方程为 ，即 ，即 ， 同理可知，直线 的方程为 ， 由于点 为这两条直线的公共点，则 ， 所以，点 、 的坐标满足方程 ， 所以，直线 的方程为 ， 联立 ，可得 ， 由韦达定理可得 ， ， 所以， ， 点 到直线 的距离为 ， 所以， ， ， 由已知可得 ，所以，当 时， 的面积取最大值 ． 4.(2021年高考全国甲卷理科·第20题)抛物线C的顶点为坐标原点O．焦点在x轴上，直线l： 交C 于P，Q两点，且 ．已知点 ，且 与l相切． (1)求C， 的方程； (2)设 是C上的三个点，直线 ， 均与 相切．判断直线 与 的位置关 系，并说明理由． 【答案】(1)抛物线 ， 方程为 ；(2)相切，理由见解析 25解析：(1)依题意设抛物线 ， ， 所以抛物线 的方程为 ， 与 相切，所以半径为 ， 所以 的方程为 ； (2)设 若 斜率不存在，则 方程为 或 ， 若 方程为 ，根据对称性不妨设 ， 则过 与圆 相切的另一条直线方程为 ， 此时该直线与抛物线只有一个交点，即不存在 ，不合题意； 若 方程为 ，根据对称性不妨设 则过 与圆 相切的直线 为 ， 又 ， ，此时直线 关于 轴对称， 所以直线 与圆 相切； 若直线 斜率均存在， 则 ， 所以直线 方程为 ， 整理得 ， 同理直线 的方程为 ， 直线 的方程为 ， 与圆 相切， 26整理得 ， 与圆 相切，同理 所以 为方程 的两根， ， 到直线 的距离为： ， 所以直线 与圆 相切； 综上若直线 与圆 相切，则直线 与圆 相切． 5.(2020年浙江省高考数学试卷·第21题)如图，已知椭圆 ，抛物线 ， 点A是椭圆 与抛物线 的交点，过点A的直线l交椭圆 于点B，交抛物线 于M(B，M不同于 A)． (Ⅰ)若 ，求抛物线 的焦点坐标； (Ⅱ)若存在不过原点的直线l使M为线段AB的中点，求p的最大值． 【答案】(Ⅰ) ；(Ⅱ) 解析：(Ⅰ)当 时， 的方程为 ，故抛物线 的焦点坐标为 ； 27(Ⅱ)设 ， 由 ， ， 由 在抛物线上，所以 ， 又 ， ， ， ． 由 即 ， 所以 ， ， ， 所以， 的最大值为 ，此时 ． 法2：设直线 ， ． 将直线 的方程代入椭圆 得： ， 所以点 的纵坐标为 ． 将直线 的方程代入抛物线 得： ， 所以 ，解得 ，因此 ， 28由 解得 ， 所以当 时， 取到最大值为 ． 6.(2022年高考全国甲卷数学(理)·第20题)设抛物线 的焦点为F，点 ，过F的直 线交C于M，N两点．当直线MD垂直于x轴时， ． (1)求C的方程； (2)设直线 与C 的另一个交点分别为A，B，记直线 的倾斜角分别为 ．当 取得 最大值时，求直线AB的方程． 【答案】(1) ； (2) ． 【解析】(1)抛物线的准线为 ，当 与x轴垂直时，点M的横坐标为p， 此时 ，所以 ，所以抛物线C的方程为 ； (2)设 ，直线 ， 由 可得 ， ， 由斜率公式可得 ， ， 直线 ，代入抛物线方程可得 ， ，所以 ，同理可得 ， 所以 又因为直线MN、AB的倾斜角分别为 ，所以 ， 若要使 最大，则 ， 设 ，则 ， 29当且仅当 即 时，等号成立， 所以当 最大时， ，设直线 ， 代入抛物线方程可得 ， ，所以 ， 所以直线 ． 7.(2019·浙江·第21题)如图，已知点 为抛物线 的焦点．过点 的直线交抛物线于 ， 两点，点 在抛物线上，使得 的重心 在 轴上，直线 交 轴于 点，且 在点 的右侧，记 ， 的面积分别为 ， ． (Ⅰ)求 的值及抛物线的准线方程； (Ⅱ)求 的最小值及此时点 的坐标． A y F G O Q x B C 【答案】 【解析】(Ⅰ)由题意得 ，即 ，所以，抛物线的准线方程为 ． (Ⅱ)设 ， ， ， ， ， ，重心 ， ， 令 ， ，则 ， 由于直线 过 ，故直线 的方程为 ， 代入 ，得： ， ，即 ， ， ， 又 ， ，重心在 轴上， ， 30， ， ， ， 直线 的方程为 ，得 ， ， 在焦点 的右侧， ， ， 令 ，则 ， ， 当 时， 取得最小值为 ，此时 ． 8.(2019·全国Ⅲ·理·第21题)已知曲线C：y= ，D为直线y= 上的动点，过D作C的两条切线， 切点分别为A，B． (1)证明：直线AB过定点： (2)若以E(0， )为圆心的圆与直线AB相切，且切点为线段AB的中点，求四边形ADBE的面积． 【答案】【答案】(1)见详解；(2)3或 ． 【官方解析】 (1)设 则 ． 由于 ，所以切线 的斜率为 ，故 整理得 ．． 设 同理可得 ． 故直线 的方程为 ． 所以直线 过定点 ． (2)由(1)得直线 的方程为 ．由 可得 ． 31于是 ， ． 设 分别为 到直线 的距离，则 ． 因此，四边形 的面积 ． 设 线段 的中点，则 ． 由于 ，而 ， 与向量 平行，所以 ．解得 或 ． 当 时， ；当 时， ． 因此，四边形 的面积为3或 ． 9.(2019·全国Ⅰ·理·第19题)已知抛物线 的焦点为 ，斜率为 的直线 与 的交点为 ， ，与 轴的交点为 ． (1)若 ，求 的方程； (2)若 ，求 ． 【答案】解：设直线 ． (1)由题设得 ，故 ，由题设可得 ． 由 ，可得 ，则 ． 从而 ，得 ．所以 的方程为 ． (2)由 可得 ． 由 ，可得 ．所以 ．从而 ，故 ． 代入 的方程得 ．故 ． 10.(2019·北京·理·第18题)已知抛物线C：x2=−2py经过点(2，−1)． (Ⅰ)求抛物线C的方程及其准线方程； (Ⅱ)设O为原点，过抛物线C的焦点作斜率不为0的直线l交抛物线C于两点M，N，直线y=−1分别 32交直线OM，ON于点A和点B．求证：以AB为直径的圆经过y轴上的两个定点． 【答案】【解析】(Ⅰ)将点 代入抛物线方程： ，可得 ， 故抛物线方程为： ，其准线方程为： ． (Ⅱ)很明显直线 的斜率存在(不为零)，焦点坐标为 ， 设直线 的方程为 ，与抛物线方程 联立可得： ． 设 ，则 ．且 ， 直线 的方程为 ，与 联立可得： ，同理可得 ， 易知以AB为直径的圆的圆心坐标为： ，圆的半径为： ， 且： ， ， 则圆的方程为： ， 令 整理可得： ，解得： ， 即以AB为直径的圆经过 轴上的两个定点 ． 考点 04 圆锥曲线的定点定值问题 1.(2021年新高考全国Ⅱ卷·第20题)已知椭圆C的方程为 ，右焦点为 ，且 离心率为 ． (1)求椭圆C的方程； (2)设M，N是椭圆C上的两点，直线 与曲线 相切．证明：M，N，F三点共线的 充要条件是 ． 【答案】解析:(1)由题意，椭圆半焦距 且 ，所以 ，又 ，所以椭 圆方程为 ； (2)由(1)得，曲线为 ，当直线 的斜率不存在时，直线 ，不合题意； 33当直线 的斜率存在时，设 ， 必要性： 若M，N，F三点共线，可设直线 即 ，由直线 与曲线 相切可得 ，解得 ，联立 可得 ，所 以 ，所以 ,所以必要性成立； 充分性：设直线 即 ，由直线 与曲线 相切可 得 ，所以 ，联立 可得 ， 所以 ，所以 ， 化简得 ，所以 ，所以 或 ，所以直线 或 ，所以直线 过点 ，M，N，F三点共线，充分性成立；所以M，N，F三点共 线的充要条件是 ． 2.(2020年高考课标Ⅰ卷理科·第20题)已知A、B分别为椭圆E： (a>1) 左、右顶点，G为E 的 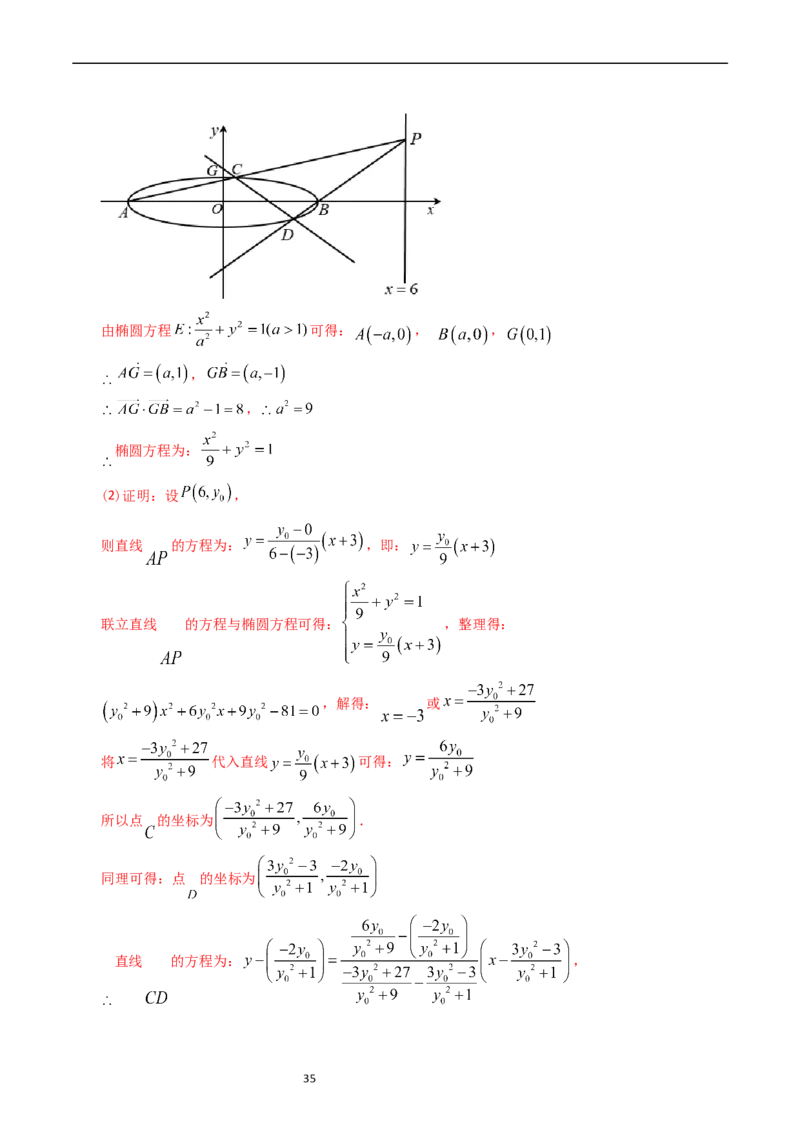的上顶点， ，P为直线x=6上的动点，PA与E的另一交点为C，PB与E的另一交点为D． (1)求E 的方程； (2)证明：直线CD过定点． 【答案】(1) ；(2)证明详见解析． 【解析】(1)依据题意作出如下图象： 34由椭圆方程 可得： ， ， ， ， 椭圆方程为： (2)证明：设 ， 则直线 的方程为： ，即： 联立直线 的方程与椭圆方程可得： ，整理得： ，解得： 或 将 代入直线 可得： 所以点 的坐标为 ． 同理可得：点 的坐标为 直线 的方程为： ， 35整理可得： 整理得： 故直线 过定点 3.(2020年新高考全国Ⅰ卷(山东)·第22题)已知椭圆C： 的离心率为 ，且过点 A(2，1)． (1)求C的方程： (2)点M，N在C上，且AM⊥AN，AD⊥MN，D为垂足．证明：存在定点Q，使得|DQ|为定值． 【答案】(1) ；(2)详见解析． 解析：(1)由题意可得： ，解得： ，故椭圆方程为： ． (2)设点 ． 因为AM⊥AN，∴ ，即 ,① 当直线MN的斜率存在时，设方程为 ,如图1． , 代入椭圆方程消去 并整理得： ②, 根据 ,代入①整理可得： 将②代入， ， 整理化简得 , ∵ 不在直线 上，∴ ， 36∴ ， 于是MN的方程为 ， 所以直线过定点直线过定点 ． 当直线MN的斜率不存在时，可得 ,如图2． 代入 得 , 结合 ,解得 , 此时直线MN过点 , 由于AE为定值，且△ADE为直角三角形，AE为斜边， 所以AE中点Q满足 为定值(AE长度的一半 )． 由于 ，故由中点坐标公式可得 ． 故存在点 ，使得|DQ|为定值． 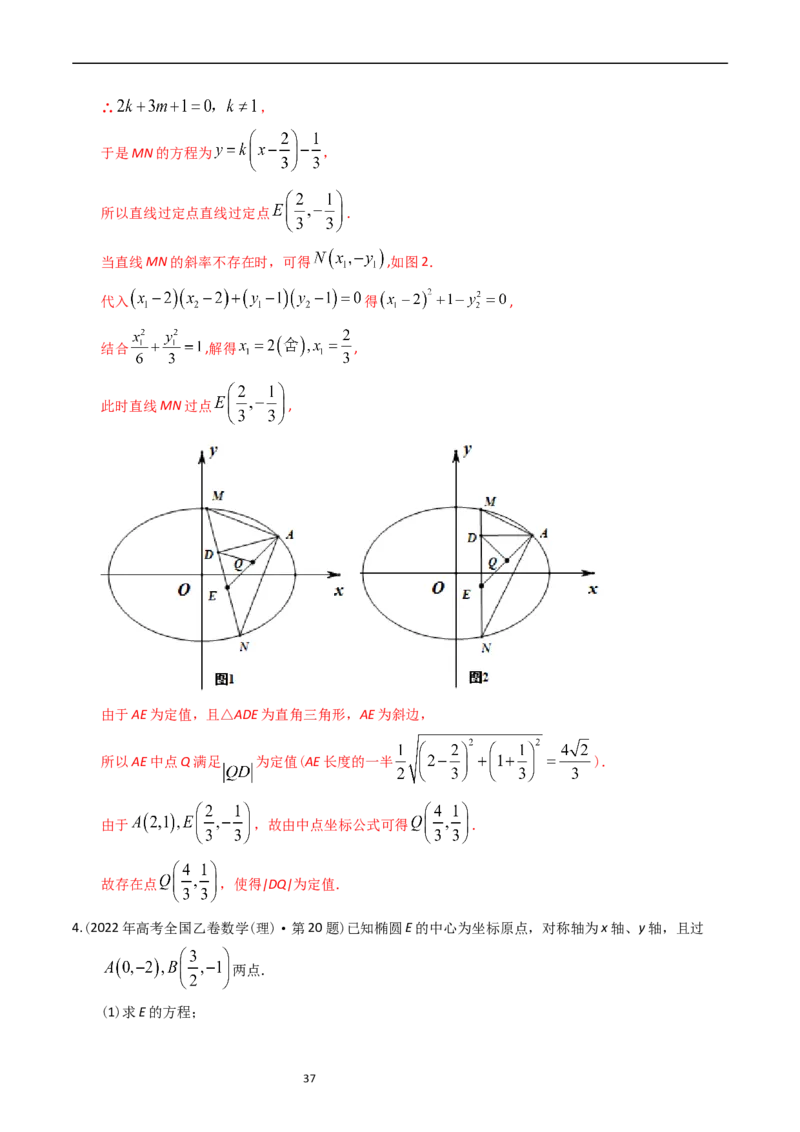4.(2022年高考全国乙卷数学(理)·第20题)已知椭圆E的中心为坐标原点，对称轴为x轴、y轴，且过 两点． (1)求E的方程； 37(2)设过点 的直线交E于M，N两点，过M且平行于x轴的直线与线段AB交于点T，点H满 足 ．证明：直线HN过定点． 【答案】(1) (2) 解析：设椭圆E的方程为 ，过 ， 则 ，解得 ， ， 所以椭圆E的方程为： ． 【小问2详解】 ，所以 ， ①若过点 的直线斜率不存在，直线 ．代入 ， 可得 ， ，代入AB方程 ，可得 ，由 得到 ．求得HN方程： ，过点 ． ②若过点 的直线斜率存在，设 ． 联立 得 ， 可得 ， ， 且 38联立 可得 可求得此时 ， 将 ，代入整理得 ， 将 代入，得 显然成立， 综上，可得直线HN过定点 考点 05 解析几何综合类问题 1.(2023年新课标全国Ⅰ卷·第22题)在直角坐标系 中，点 到 轴的距离等于点 到点 的距 离，记动点 的轨迹为 ． (1)求 的方程； (2)已知矩形 有三个顶点在 上，证明：矩形 的周长大于 ． 【答案】(1) (2)见解析 解析：(1)设 ,则 ，两边同平方化简得 ， 故 ． (2)法一：设矩形的三个顶点 在 上,且 ，易知矩 形四条边所在直线的斜率均存在，且不为0， 39则 ,令 ， 同理令 ，且 ，则 ， 设矩形周长为 ,由对称性不妨设 ， ， 则 ． ， 易知 则令 , 令 ，解得 ， 当 时， ，此时 单调递减， 当 ， ，此时 单调递增， 则 ， 故 ,即 ． 当 时, ,且 ，即 时等号成立，矛盾， 故 , 40得证． 法二：不妨设 在 上，且 ， 依题意可设 ，易知直线 ， 的斜率均存在且不为0， 则设 , 的斜率分别为 和 ，由对称性，不妨设 ， 直线 的方程为 ， 则联立 得 ， ，则 则 ， 同理 ， 令 ，则 ，设 ， 则 ，令 ，解得 ， 当 时， ，此时 单调递减， 41当 ， ，此时 单调递增， 则 ， ， 但 ，此处取等条件为 ，与最终 取等时 不一致，故 ． 法三：为了计算方便,我们将抛物线向下移动 个单位得抛物线 , 矩形 变换为矩形 ,则问题等价于矩形 的周长大于 ． 设 , 根据对称性不妨设 ． 则 , 由于 , 则 ． , 由于 且 介于 之间, 则 ． 令 , ,则 ,从而 故 ①当 时, ②当 时,由于 ,从而 , 42从而 又 , 故 ,由此 ， 当且仅当 时等号成立，故 ，故矩形周长大于 ． ． 2 .(2023年全国乙卷理科·第20题)已知椭圆 的离心率是 ，点 在 上． (1)求 方的程； (2)过点 的直线交 于 两点，直线 与 轴的交点分别为 ，证明：线段 的中点为定点． 【答案】(1) (2)证明见详解 解析：(1)由题意可得 ，解得 ， 43所以椭圆方程为 ． (2)由题意可知：直线 的斜率存在，设 ， 联立方程 ，消去y得： ， 则 ，解得 ， 可得 ， 因为 ，则直线 ， 令 ，解得 ，即 , 同理可得 ， 则 ， 所以线段 的中点是定点 ． 443 .(2020年高考课标Ⅱ卷理科·第19题)已知椭圆C ： (a>b>0) 右焦点F与抛物线C 的焦点 1 的2 重合，C 的中心与C 的顶点重合．过F且与x轴垂直的直线交C 于A，B两点，交C 于C，D两点， 1 2 1 2 且|CD|= |AB|． (1)求C 的离心率； 1 (2)设M是C 与C 的公共点，若|MF|=5，求C 与C 的标准方程． 1 2 1 2 【答案】(1) ；(2) ， ． 解析：(1) ， 轴且与椭圆 相交于 、 两点， 则直线 的方程为 ， 联立 ，解得 ，则 ， 抛物线 的方程为 ，联立 ， 45解得 ， ， ，即 ， ， 即 ，即 ， ，解得 ，因此，椭圆 的离心率为 ； (2)由(1)知 ， ，椭圆 的方程为 ， 联立 ，消去 并整理得 ， 解得 或 (舍去)， 由抛物线的定义可得 ，解得 ． 因此，曲线 的标准方程为 ， 曲线 的标准方程为 ． 4.(2019·天津·理·第18题)设椭圆 的左焦点为 ，上顶点为 ．已知椭圆的短轴 长为4，离心率为 ． (Ⅰ)求椭圆的方程； (Ⅱ)设点 在椭圆上，且异于椭圆的上、下顶点，点 为直线 与 轴的交点，点 在 轴的负 半轴上．若 ( 为原点)，且 ，求直线 的斜率． 【答案】本小题主要考查椭圆的标准方程和几何性质、直线方程等基础知识。考查用代数方法研究圆 锥曲面的性质．考查运算求解能力，以及用方程思想解决问题的能力．满分13分． (Ⅰ)解：设椭圆的半焦距为 ，依题意， ，又 ，可得 ， ． 所以，椭圆的方程为 ． 46(Ⅱ)解：由题意，设 ．设直线 的斜率为 ，又 ， 则直线 的方程为 ，与椭圆方程联立 整理得 ， 可得 ，代入 得 ，进而直线 的斜率 ． 在 中，令 ，得 ．由题意得 ，所以直线 的斜率为 ． 由 ，得 ，化简得 ，从而 ． 所以，直线 的斜率为 或 ． 5.(2019·全国Ⅱ·理·第21题)已知点 ， ，动点 满足直线 与 的斜 率之积为 ．记 的轨迹为曲线 ． 求 的方程，并说明 是什么曲线； 过坐标原点的直线交 于 两点，点 在第一象限， 轴，垂足为 ，连结 并延长 交 于点 ． 证明： 是直角三角形； 求 面积的最大值． 【答案】【答案】 详见解析 详见解析 【官方解析】 由题设得 ，化简得 ，所以 为中心在坐标原点，焦点在 轴上的椭圆，不含左右顶点． 设直线 的斜率为 ，则其方程为 ．由 得 ． 记 ，则 ． 于是直线 的斜率为 ，方程为 ． 47由 ，得 ．① 设 ，则 和 是方程①的解，故 ，由此得 ． 从而直线 的斜率为 ．所以 ，即 是直角三角形． 由 得 ， ， 所以 的面积 ． 设 ，则由 得 ，当且仅当 时取等号． 因为 在 单调递减，所以当 ，即 时， 取得最大值，最大值为 ． 因此， 面积的最大值为 ． 【分析】 分别求出直线 与 的斜率，由已知直线 与 的斜率之积为 ，可以得 到等式，化简可以求出曲线 的方程，注意直线 与 有斜率的条件； 设出直线PQ的方程，与椭圆方程联立，求出 两点的坐标，进而求出点E的坐标，求出 直线QE的方程，与椭圆方程联立，利用根与系数关系求出G的坐标，再求出直线PG的斜率，计算 的值，就可以证明出 是直角三角形； 由 可知P,Q,G三点坐标， 是直角三角形，求出 的长，利用面积公式求出 的面积，利用导数求出面积的最大值. y y 【解析】 直线 的斜率为 (x2)，直线 的斜率为 (x2)，由题意可知： AM x2 BM x2 y y 1    x2 2y2 4,(x2)，所以曲线 是以坐标原点为中心，焦点在 轴上，不 x2 x2 2 x 48x2 y2 包括左右两顶点的椭圆，其方程为  1,x2 ； 4 2 设直线PQ的方程为y kx,由题意可知k 0,直线PQ的方程与椭圆方程x2 2y2 4联立,  2  2 x , x ,   y kx,  2k2 1  2k2 1 即  或 ,点 在第一象限，所以 x2 2y2 4.  2k  2k y  . y  .   2k2 1   2k2 1 2 2k 2 2k 2 P( , ),Q( , ) ( ,0) ，因此点 的坐标为 2k2 1 2k2 1 2k2 1 2k2 1 E 2k2 1 k k k 直线 的斜率为k  ，可得直线 方程： y  x ，与椭圆方程联立， QE QE 2 QE 2 2k2 1  k k y  x ,   2 2k2 1 ，消去 得， 4k2x 12k2 8 (*)，设点 ，显然 (2k2)x2   0  x2 2y2 4. y 2k2 1 2k2 1 G(x ,y ) 1 1 2 点的横坐标 和 是方程(*)的解 Q 2k2 1 x 1 12k2 8  所以有x  2  2k2 1  x  6k2 4 ，代入直线 方程中，得 1 2k2 1 2k2 1 (k2 2) 2k2 1 QE 6k2 4 2k3 ( , ) 2k3 ，所以点 的坐标为 (k2 2) 2k2 1 (k2 2) 2k2 1 ， y  1 (k2 2) 2k2 1 G 2k3 2k  (k2 2) 2k2 1 2k2 1 2k3 2k(k2 2) 1 直线 的斜率为；k    ， PG 6k2 4 2 6k2 42(k2 2) k  PG (k2 2) 2k2 1 2k2 1 因为 ，所以 ，因此 是直角三角形； PQ  PG 2 2k 2 2k P( , ),Q( , ) 由 可知： ， 2k2 1 2k2 1 2k2 1 2k2 1 的坐标为 ， G 492 2 2k 2k 4 1k2 PQ (  )2 (  )2  ， 2k2 1 2k2 1 2k2 1 2k2 1 2k2 1 6k2 4 2 2k3 2k 4k k21 PG  (  )2(  )2  , (k2 2) 2k21 2k21 (k22) 2k21 2k21 (k22) 2k21 1 4k k2 1 4 1k2 8(k3k) S     ， ， PQG 2 (k2 2) 2k2 1 2k2 1 2k4 5k2 2 因为 ，所以当 时， ，函数 单调递增，当 时， ，函数 单调 递减，因此当 时，函数 有最大值，最大值为 . 6.(2019·江苏·第 17 题)如图，在平面直角坐标系 中，椭圆 : 的焦点为 ， ．过 作 轴的垂线 ，在 轴的上方， 与圆 : 交于点 ，与 椭圆 交于点 .连结 并延长交圆 于点 ，连结 交椭圆 于点 ，连结 ． 已知 ． (1)求椭圆 的标准方程； (2)求点 的坐标． 【答案】【答案】见解析 【解析】(1)设椭圆 的焦距为 因为 ， ，所以 ， 又因为 ， 轴，所以 因此， ，从而 由 ，得 50因此，求椭圆 的标准方程为 (2)解法一： 由(1)知，椭圆 ： ， 因为 ⊥ 轴，所以点 的横坐标为1. 将 代入圆 的方程 ，解得 因为点 在 轴上方，所以 . 又 ，所以直线 ： . 由 ，得 ， 解得 或 . 将 代入 ，得 ， 因此 .又 ，所以直线 ： . 由 ，得 ，解得 或 . 又因为 是线段 与椭圆的交点，所以 . 将 代入 ，得 .因此 . 解法二：由(1)知，椭圆C： .如图，连结 51因为 ， ，所以 ，从而 因为 ，所以 ， 所以 ，从而 . 因为 轴，所以 轴. 因为 ，由 ，得 . 又因为 是线段 与椭圆的交点，所以 . 因此 . 52