黑龙江省鹤岗市第一中学2022-2023学年高三上学期开学考试数学答案(1)_2023年8月_028月合集_2023届黑龙江省鹤岗市第一中学高三上学期开学考试

数学参考答案 1.A 2．D 3．D 4．A 5．C 6．C 7．D 8．B 9．AB 10．ABCD 11．ABD 12．BCD 13． 14．0 15． 16． 17.(1) 所以最小正周期 , (2)(-1,2] (3)∵ ，∴ ∵ ∴ ，∴ . 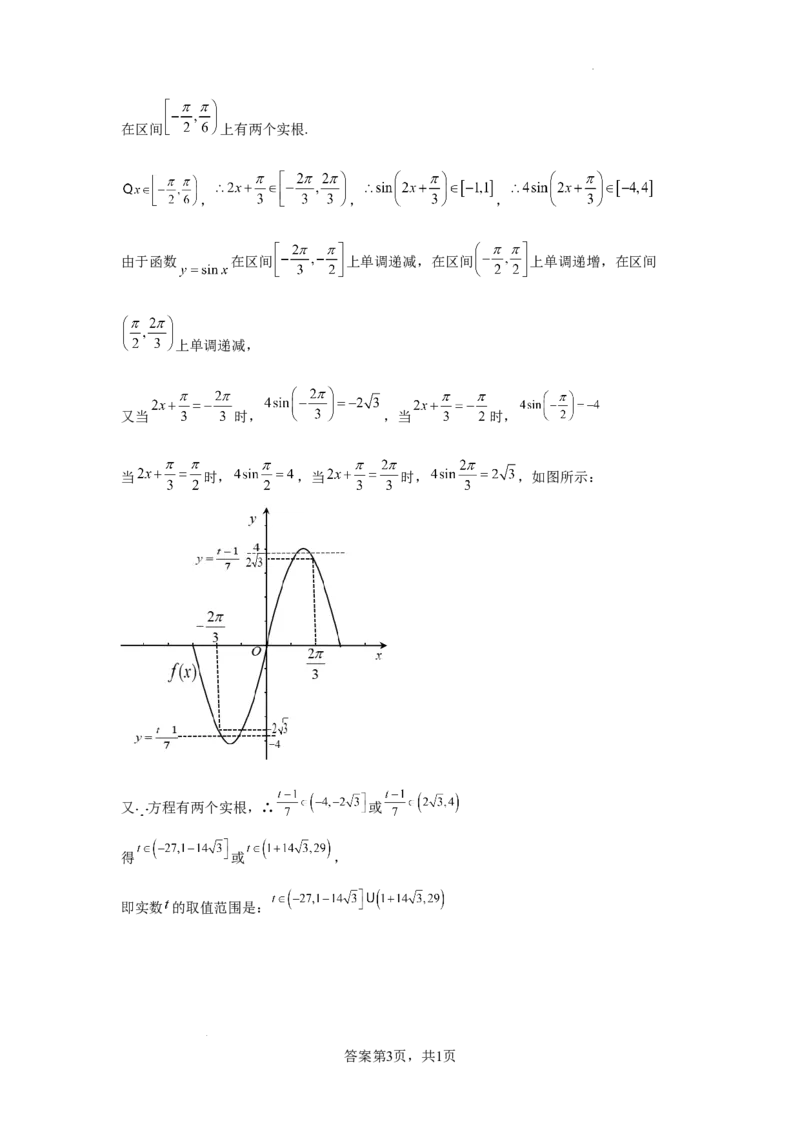18（Ⅰ）由 得，当 时， 答案第1页，共1页 学科网（北京）股份有限公司两式作差得： ，即 ，即 ， 令 得 ，所以 是以 为首项， 为公比的等比数列． 所以 ，故 ． 答案第2页，共1页 学科网（北京）股份有限公司（Ⅱ）由（Ⅰ）知 ， 两式作差得： 所以 ． 19．（1） ， 由 ，可得 ，所以 ， 经检验，满足题意． （2）因为 在 上单调递增，所以 在 上恒成立， 即 在 上恒成立． 令 ， ， 则 ， 因为 ，所以 ， 所以 ，所以 ． 所以实数a的取值范围为 ． 20（1）由题意知 ， ，得周期 ，∴ 答案第2页，共1页 学科网（北京）股份有限公司当 时， 取得最大值4，即 ， 得 ，得 ， 又 ， 当 时， ， 即 ． （2）由已知 在区间 上有两个实根，即方程 答案第3页，共1页 学科网（北京）股份有限公司在区间 上有两个实根. ， ， ， 由于函数 在区间 上单调递减，在区间 上单调递增，在区间 上单调递减， 又当 时， ，当 时， 当 时， ，当 时， ，如图所示： 又 方程有两个实根，∴ 或 得 或 ， 即实数 的取值范围是： 答案第3页，共1页 学科网（北京）股份有限公司21．（1）根据题意得： ，解得 ， ， ，抛物线焦点 ， 因此椭圆 ，拋物线 （2）设 ，联立 与椭圆 ， 整理得： ， 答案第4页，共1页 学科网（北京）股份有限公司判别式： 弦长公式： 所以 联立 与抛物线 ，整理得： ，判别式： 弦长公式： ， 所以 ， 因为 ，因此 ，解得： 在 轴上截距 或 ，因此在 轴上截距取值范 . 22(1) 的定义域为 ， ，当 时， 恒成立，故 在 上单调递减；当 时，令 得： ，令 得： ，故 在 上单调递增，在 上单调递减； 综上：当 时， 在 上单调递减；当 时， 在 上单调递增， 在 上单调递减； (2)由（1）可知，要想 有两个相异的零点 ，则 ，不妨设 ，因为 答案第4页，共1页 学科网（北京）股份有限公司，所以 ，所以 ，要证 ，即证 ，等价于 ，而 ，所以等价于证明 ，即 ， 令 ，则 ，于是等价于证明 成立， 答案第5页，共1页 学科网（北京）股份有限公司设 ， ，所以 在 上单调递增， 故 ，即 成立， 所以 ，结论得证. . 答案第5页，共1页 学科网（北京）股份有限公司