黑龙江省鹤岗市第一中学2022-2023学年高三上学期开学考试数学试题(1)_2023年8月_028月合集_2023届黑龙江省鹤岗市第一中学高三上学期开学考试

鹤岗市第一中学 2022--2023 年度上学期开学考试 7．将函数 fx2cosx的图象先向右平移0个单位长度，再把所得函数图象的
1
高三数学试题 横坐标变为原来的 0倍，纵坐标不变，得到函数gx的图象，若对gx满足

一、单选题（本题共8个小题，每题 5 分，共 40分，在每小题给出的四个选项中，只 gx gx  4，有 x x   恒成立，且g  x 在区间(  ，  )上单调递减，则的取
1 2 1 2 min 4 6 3
有一项是符合题目要求的）
值范围是（ ）
1．已知集合M 
x,yx2y22,xZ,yZ 
，则集合M 的真子集的个数（ ）
   
A．[ ， ] B．[ ，]
A． 29 1 B． 28 1 C． 25 D． 24 1 12 3 3 2
 2  2
1 C．( ， ] D．[ ， ]
2.已知tan(π)  2，则  （ ） 3 3 3 3
1 cos2
1 5 8．设函数 f x的定义域为 R ，满足 f(x2)2f(x)，且当x2,0时，f(x)2x(x2)．若
A．-3 B． C．2 D．
2 6
3
对任意xm,，都有 f(x) ，则m的取值范围是（ ）
3．下列函数中，在，0 上单调递减的是（ ） 4
2  3  1  3 
A． y  2sinx B．y 2x3 A．  3 ,  B．  2 ,  C．  2 ,  D．  4 , 
x1
二、多选题（本题共 4个小题，每题 5分，共 20分）
 1 
C．ylog   D． y  x2 4x  
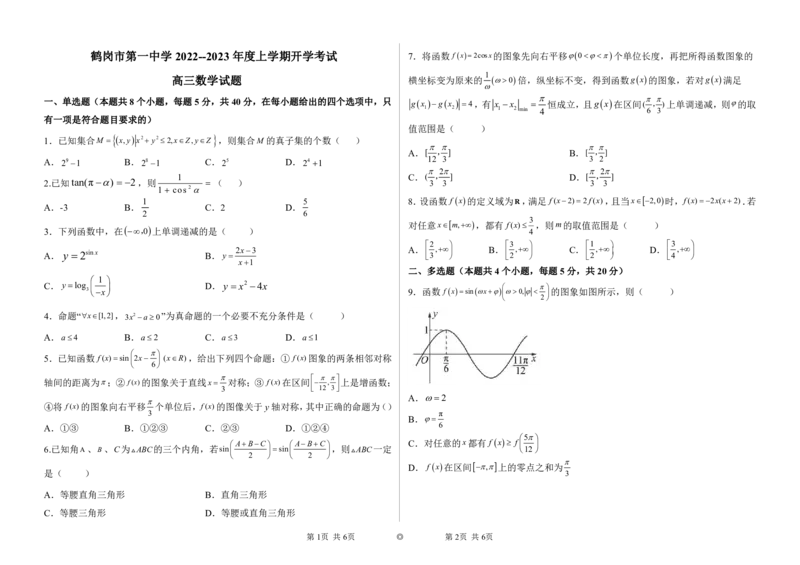
3x 9．函数 f xsinx 0,  的图象如图所示，则（ ）
 2
4．命题“x[1,2]， 3x2a0”为真命题的一个必要不充分条件是（ ）
A．a4 B．a2 C．a3 D．a1
 
5．已知函数 f(x)sin2x  (xR)，给出下列四个命题：① f(x)图象的两条相邻对称
 6
   
轴间的距离为；② f(x)的图象关于直线x 对称；③ f(x)在区间   ,  上是增函数；
3  12 3
A．2

④将 f(x)的图象向右平移 个单位后，f(x)的图像关于y轴对称，其中正确的命题为（）
3 π
B．
A．①③ B．①②③ C．②③ D．①②④ 6
5
 ABC  ABC C．对任意的x都有 f x f 
6.已知角 A 、 B 、C为ABC的三个内角，若sin sin  ，则ABC一定 12 
 2   2 

D． f x在区间,上的零点之和为
是（ ） 3
A．等腰直角三角形 B．直角三角形
C．等腰三角形 D．等腰或直角三角形
第1页 共6页 ◎ 第2页 共6页10．下列说法错误的是（ ） 三．填空题（本题共 4个小题，每小题 5分，共20分）
A.f (x)  ax2021 2021(a 0且a 1)的图象过定点A,则A的坐标为（2021，2021） 13．计算：sin330cos240______．
14．已知 f x是定义在 R 上的偶函数，gx是定义在 R 上的奇函数，且gx f(x1)，
4
B.y sinx (0 x)的最小值是4
sinx 则 f(2021) f(2023)的值为______________.
π  3π
C.不等式mx2 mx10对一切xR恒成立，则m的范围是（0，4） 15．已知 f(x)2sin(2x 3 )，若x 1 ,x 2 ,x 3   0, 2   ，使得 f(x 1 ) f(x 2 ) f(x 3 )，若x 1 x 2 x 3 的
 最大值为M，最小值为N，则M N ___________.
f(x)sin2x2cos2 x关于（ ，0）中心对称
D.
8
16．若关于x的不等式ex alnxa恒成立，则实数a的取值范围为__________．
1
11.已知等比数列a 的前n项和为S ，且S 4a ，a 是a 1与 a 的等差中项， 四．解答题（本题共 6个小题，共 70分,解答应写出文字说明、证明过程或演算步骤）
n n 2 1 2 1 2 3
 
17．（10分）已知函数 f x 3cos2x 2sin2x1．
a  2
数列b 满足b  n ，数列b 的前n项和为T ，则下列命题正确的是（ ）
n n S S n n
n n1 (1)求函数 f x的最小正周期;
A．数列a 的通项公式a 23n1
n n

(2)当x(0, )时，求 f x的值域;
B．s 3n 1 2
n
C．数列b n 的通项公式为b n   3n 1 2    3 3 n n 11  (3)若x    0,  6    且 f x 1 2 ，求 f    x 1  2    的值．
1 1
D．T 的取值范围是  , 
n 8 6
12．已知函数 f  x lg

x2 2x2x1

，g  x 
2x 6
则下列说法正确的是（ ）
2x 2 18．（12分）设数列a 的前n项和为S ，若S a n  nN ．
n n n n
A． f  x 是奇函数
（Ⅰ）证明a 1为等比数列并求数列 a 的通项公式；
n n
B．g  x 的图象关于点 1，2 对称
（Ⅱ）设b  2n1  1a ，数列 b 的前n项和为T ，求T .
n n n n n
C．若函数F  x  f  x g  x 在x 1m,1m 上的最大值、最小值分别为M 、N ，则
M N 4
D．令F  x  f  x g  x ，若F  a F 2a1 4，则实数a的取值范围是1,
第3页 共6页 ◎ 第4页 共6页19．（12分已知 f(x)sinxcosxax，其中aR．
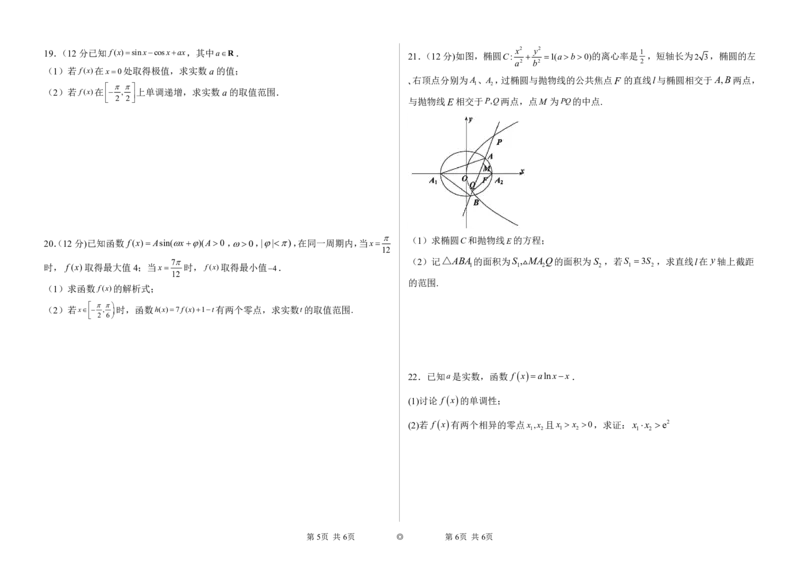
21．（12分)如图，椭圆C:
x2

y2
1(ab0)的离心率是
1
，短轴长为2 3，椭圆的左
a2 b2 2
（1）若 f(x)在x0处取得极值，求实数a的值；
､右顶点分别为A、A ，过椭圆与抛物线的公共焦点F 的直线l与椭圆相交于A,B两点，
   1 2
（2）若 f(x)在

 ,

上单调递增，求实数a的取值范围．
 2 2 与抛物线E相交于P,Q两点，点M 为PQ的中点.
20．（12分)已知函数 f(x) Asin(x)(A0 ，0，||)，在同一周期内，当x
 （1）求椭圆C和抛物线E的方程；
12
7 （2）记△ABA的面积为S ,MAQ的面积为S ，若S 3S ，求直线l在 y轴上截距
时， f (x)取得最大值4；当x 时， f(x)取得最小值4． 1 1 2 2 1 2
12
的范围.
（1）求函数 f(x)的解析式；
  
（2）若x   ,  时，函数h(x)7f(x)1t有两个零点，求实数t的取值范围．
 2 6
22．已知a是实数，函数 f  x alnxx．
(1)讨论 f  x 的单调性；
(2)若 f  x 有两个相异的零点x ,x 且x  x 0，求证：x x e2
1 2 1 2 1 2
第5页 共6页 ◎ 第6页 共6页答案第1页，共1页