文档内容
五年(2019-2023)年高考真题分项汇编
专题 13 不等式
不等式作为高考一个工具,主要题型是小题,再者就是与其他知识点相结合。
考点01 解基本不等式
考点02 不等式应用—线性规划
考点04 不等式综合应用
考点 01:解基本不等式
填空题
1.(2021高考天津)若 ,则 的最小值为____________.
2.(2020天津高考·)已知 ,且 ,则 的最小值为_________.
3.(2020江苏高考·)已知 ,则 的最小值是_______.
4.(2019·天津·理)设 ,则 的最小值为 .
5.(2019·上海)若 ,且 ,则 的最大值为________.
6.(2019·江苏·)在平面直角坐标系 中, 是曲线 上一动点,则点 到直线
的距离最小值是______.
7.(2022年全国高考甲卷数学(文)·)已知 中,点D在边BC上, .当
取得最小值时, ________.
1考点03:不等式应用—线性规划
1.(2021年高考浙江卷·)若实数x,y满足约束条件 ,则 的最小值是 ( )
A. B. C. D.
2.(2021年全国高考乙卷文科·)若 满足约束条件 则 的最小值为 ( )
A.18 B.10 C.6 D.4
3.(2020年浙江省高考数学试卷·)若实数x,y满足约束条件 ,则z=2x+y的取值范围是 (
)
A. B. C. D.
4.(2022年浙江省高考数学试题·)若实数x,y满足约束条件 则 的最大值是 (
)
A.20 B.18 C.13 D.6
5.(2022年高考全国乙卷(文))若x,y满足约束条件 则 最大值是 ( )
的
A. B.4 C.8 D.12
6.(2019·浙·)若实数 , 满足约束条件 则 的最大值是 ( )
A. B. C. D.
7.(2019·天津·文·)设变量 满足约束条件 则目标函数 的最大值为 ( )
A.2 B.3 C.5 D.6
二 填空题
21.(2023年全国乙卷文科·)若x,y满足约束条件 ,则 的最大值为______.
2.(2023年全国甲卷文科·)若x,y满足约束条件 ,设 的最大值为____________.
3.(2020年高考课标Ⅰ卷文科·若x,y满足约束条件 则z=x+7y的最大值为______________.
4.(2020年高考课标Ⅱ卷文科·)若x,y满足约束条件 则 的最大值是__________.
,
5.(2020年高考课标Ⅲ卷文科·第13题)若x,y满足约束条件 ,则z=3x+2y的最大值为
_________.
5.(2019·上海·文理)已知 满足 ,求 的最小值为________.
7.(2019·全国Ⅱ·文·)若变量 满足约束条件 则 的最大值是___________.
考点04 不等式综合应用
1.(2023年全国乙卷文科·)已知实数 满足 ,则 的最大值是 ( )
A. B.4 C. D.7
2.(2019·天津·理) , 的大关系为 ( )
A. B. C. D.
33.(2020年浙江省高考数)已知a,b R且ab≠0,若(x–a)(x–b)(x–2a–b)≥0在x≥0上恒成立,则
( )
A.a<0 B.a>0 C.b<0 D.b>0
4.(2020年浙江省高考数学试卷·)已知a,b R且ab≠0,若(x–a)(x–b)(x–2a–b)≥0在x≥0上恒成立,则 (
)
A.a<0 B.a>0 C.b<0 D.b>0
5.(2019·全国Ⅰ·理) 已知 , , ,则 ( )
A. B. C. D.
二、填空题
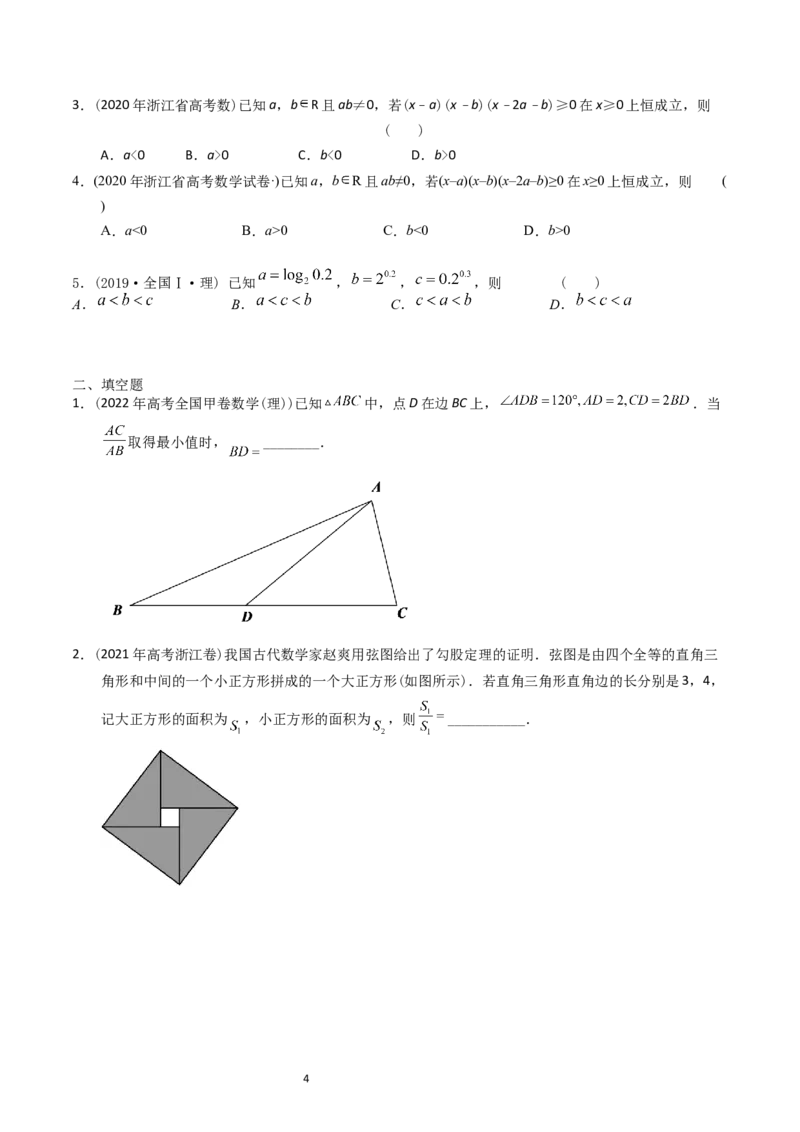
1.(2022年高考全国甲卷数学(理))已知 中,点D在边BC上, .当
取得最小值时, ________.
2.(2021年高考浙江卷)我国古代数学家赵爽用弦图给出了勾股定理的证明.弦图是由四个全等的直角三
角形和中间的一个小正方形拼成的一个大正方形(如图所示).若直角三角形直角边的长分别是3,4,
记大正方形的面积为 ,小正方形的面积为 ,则 ___________.
4