文档内容
【赢在高考·黄金8卷】备战2024年高考数学模拟卷(新高考七省专用)
黄金卷
(考试时间:120分钟 试卷满分:150分)
第 I 卷(选择题)
一、单项选择题:本题共8小题,每小题5分,共40分,在每小题给出的四个选项中,只有一项是符合要
求的。
1.已知集合 ,则 是( )
A. B. C. D.
【答案】C
【解析】由 可得 ,
所以 故选:C
2.已知复数 满足 ,则 ( )
A. B. C. D.
【答案】B
【解析】因为复数 满足 ,所以 ,
所以 .故选:B.
3.已知向量 , , ,若 ,则 ( )
A.3 B.-1 C.2 D.4
【答案】A
【解析】由 , ,
又由 ,可得: ,解得 .故选:A.
4.已知角 满足 ,则 的值为( )
A. B. C. D.
【答案】D
【解析】由 ,可得 ,所以 ,
.故选:D.
5.第19届亚运会在杭州举行.杭州市奥林匹克体育中心是杭州亚运会比赛场馆之一,主要由主体育场、
游泳馆、网球中心以及综合训练馆组成.现从甲、乙等7名服务者中随机选取4人分别到这四个区域负责
服务工作,要求这四个区域各有1名服务者,且甲不去游泳馆,乙不去网球中心,则不同的安排方案共有
( )
A.360种 B.480种 C.620种 D.720种
【答案】C
【解析】由题意按甲、乙是否被选中分为三种情况:
①若甲、乙都未被选中,则不同的安排方案有 (种);
②若甲、乙2人中只有1人被选中,则不同的安排方案有 (种);
③若甲、乙都被选中,则先安排甲,再安排乙,
若甲去了网球中心,则不同的安排方案有 (种);
若甲没有去网球中心,则不同的安排方案有 (种).
所以当甲、乙都被选中时,不同的安排方案有 (种).
由分类加法计数原理可得共有 (种)不同的安排方案.故选:C.
6.已知直线 ,若无论 取何值,直线 与圆 恒有公共点,则
的取值范围是( )
A. B. C. D.
【答案】A
【解析】将直线 化为 ,故直线 恒过定点 ,
又直线 与圆 恒有公共点,
所以点 在圆上或圆内,即 ,
又 ,所以 ,即 的取值范围为 ,故选:A.
7.等差数列 中的前 项和分别为 ,则 ( )
A. B. C. D.
【答案】D
【解析】 等差数列 中的前 项和分别为 ,.故选:D.
8.如图,已知 , 是双曲线C: 的左、右焦点,P,Q为双曲线C上两点,满足 ,
且 ,则双曲线C的离心率为( )
A. B. C. D.
【答案】B
【解析】延长 与双曲线交于点P',因为 ,根据对称性知 ,
设 ,则 , ,
可得 ,即 ,
所以 ,则 , ,
即 ,可知 ,
在 中,由勾股定理得 ,
即 ,解得 .故选:B
二、多项选择题:本题共4小题,每小题5分,共20分,在每小题给出的四个选项中,有多项符合题目的
要求,全部选对的得5分,部分选对的得2分,有选错的得0分。
9.举世瞩目的第19届亚运会于9月23日至10月8日在杭州举行,亚运会点燃了国人激情,也将一股运
动风吹到了大学校园.为提升学生身体素质,倡导健康生活方式,某大学社团联合学生会倡议全校学生参与
“每日万步行”健走活动.下图为该校甲、乙两名同学在同一星期内每日步数的拆线统计图,则(
)A.这一星期内甲、乙的日步数的中位数都为12600
B.这一星期内甲的日步数的平均数大于乙的日步数的平均数
C.这一星期内乙的日步数的方差大于甲的日步数的方差
D.这一星期内乙的日步数的下四分位数是12200
【答案】ABD
【解析】由折线图可得甲一星期内的步数从小到大的排列为:
11000,11800,12200,12600,13500,15400,18200,所以中位数为12600;
由折线图可得乙一星期内的步数从小到大的排列为:
11800,12200,12400,12600,15000,13800,14000,所以中位数为12600,
故这一星期内甲、乙的日步数的中位数都为12600, 正确;
这一星期内甲的日步数的平均数为: ,
这一星期内乙的日步数的平均数为: ,
因为 ,故 正确;
由图知,甲的波动程度较大,故方差较大,故 错误;
乙一星期内的步数从小到大的排列为:11800,12200,12400,12600,15000,13800,14000,
,故这一星期内乙的日步数的下四分位数是12200,故 正确;故选:
10.已知 ,直线 ,且 ,则( )
A. B. C. D.
【答案】ABD
【解析】 ,且 ,
所以 ,当且仅当 时等号成立,故A正确;
,当且仅当 时等号成立, ,故B正确;
,故C错误;,当且仅当 ,即 时等号成立,故D正确.
故选:ABD.
11.如图,正方体 的棱长为4,点E、F、G分别在棱 、 、 上,满足
, ,记平面 与平面 的交线为 ,则( )
A.存在 使得平面 截正方体所得截面图形为四边形
B.当 时,三棱锥 体积为
C.当 时,三棱锥 的外接球表面积为
D.当 时,直线 与平面 所成的角的正弦值为
【答案】BD
【解析】设正方体的棱长为4,以 为原点,以 、 、 所在的直线分别为 轴, 轴, 轴,
建立空间直角坐标系,如图所示:
对于A选项, 时, 在 点, ,
由 可知 ,所以截面 即为四边形 ;
由图形知,截面 为五边形或六边形.故A错误.对于B选项,当 时, ,
所以 ,所以 平面 , ,
又 平面 ,所以 ,
三棱锥 体积为 ,故B正确.
对于C选项,当 时, 且 平面 ,
所以根据球的性质容易判断,三棱锥 的外接球的球心在过线段 的中点,
且垂直于平面 的直线上, , ,
所以 的中点 ,可记球心 , ,
外接球的半径 ,解得 , ,
所以三棱锥 的外接球表面积为 ,故C错误.
对于D选项,当 时, , , , , ,
所以 , , ,设平面 的一个法向量为 ,
则 ,令 ,则 , ,所以可取 ,
由 平面 知,平面 的法向量为 ,
记平面 与平面 的交线 的一个方向向量为 ,
则 ,令 ,则 , ,所以可取 ,
又平面 的法向量为 ,则 , , ,
设 与平面 所成的角为 ,则 ,故D正确.故选:BD.
12.已知函数 , 的定义域均为 , 为 的导函数,且 ,
,若 为奇函数,则( )
A. B. C. D.
【答案】ABD
【解析】已知函数 , 的定义域均为 ,
因为 , ,可得 ,
又因为 为奇函数,则 ,可得 ,即 为偶函数,
则 ,即 ,可得 ,
所以 ,可知 的周期为8.
对于选项A:因为 ,
令 ,则 , ,可得 , ,故A正确;
对于选项B:因为 ,令 ,可得 ,故B正确;
对于选项C:因为 ,且 为偶函数,则 ,
令 ,可得 ,
又因为 ,令 ,则 , ,
可得 ,可得 ,
但由题设条件无法推出 ,故C错误;
对于选项D:因为 的周期为8,故 ,故D正确;故选:ABD.
第 II 卷(非选择题)
三、填空题:本题共4小题,每小题5分,共20分。
13. 的展开式中 的系数为 ,则 的值为 .
【答案】
【解析】由 可知其展开式的通项为 , , ,令 ,得 ,可得 ,
又 的系数为 ,即 , .
14.设动点 在抛物线 上,点 在 轴上的射影为点 ,点 的坐标是 ,则 的最
小值是 .
【答案】
【解析】抛物线 的焦点 ,准线方程为 ,
延长PM交准线于N,连PF,显然 垂直于抛物线的准线,
由抛物线定义知: ,
当且仅当点 是线段 与抛物线的交点时取等号,
而 ,所以 的最小值为 .
15.已知函数 ,曲线 的一个对称中心为 ,一条对称轴为
,则 的最小值为 .
【答案】9
【解析】因为 为 的一个对称中心, 为 的一条对称轴,
, 得 ,
, , 代入①得 ,
, 当 , 时, .
16.若函数 在 处的切线与 的图像有三个公共点,则 的取值范围
.【答案】
【解析】当 时, ,所以切点的坐标为 ,
当 时, , ,
所以切线的斜率 ,所以切线 的方程为:
而 ,即 过点
当切线 过点 时,切线与 函数 的图象有三个公共点,
将 代入切线方程得: ,得
当切线 与 相切时,切线 与数 的图象只有两个公点,
设切线 : 与 在 处相切,
由 ,得 ,
所以 ,得 , ,所以切点坐标为
代入切线 : ,得 ,
因此在 处的切线与 的图像有三个公共点时, 的取值范围为: .
四、解答题:本题共6小题,共70分,解答应写出必要的文字说明、证明过程及验算步骤。
17.(10分)
已知正项等差数列 的前n项和为 ,且 成等比数列.
(1)求数列 的通项公式:
(2)令 ,求 的前n项和 .
【答案】(1) ;(2)
【解析】(1)设等差数列 的公差为 ,
因为 ,则 ,
又因为 成等比数列,可得 ,则 ,解得 或 (舍去),
所以 .
(2)由(1)可得: ,
则 ,
可得 ,
两个等式相减得, ,
所以 ,
所以 .
18.(12分)
已知 的内角 , , 的对边分别为 、 、 , .
(1)求 ;
(2)已知 为 边上的中线, , ,求 的面积.
【答案】(1) ;(2)
【解析】(1) ,
由 , , , ,
所以 ,即 ,
由于 ,所以 .
(2)在 中,由 ,得 ,
由 ,得 , .
则 ,
由正弦定理得, ,
设 , ,由余弦定理得 ,故 ,在 中,由余弦定理得, ,
即 ,解得 ,则 ,
所以 的面积 .
19.(12分)
如图,在四棱锥 中, , , , ,且 .
(1)若 平面 ,证明:点 为棱 的中点;
(2)已知二面角 的大小为 ,求:平面 和平面 夹角的余弦值.
【答案】(1)证明见解析;(2)
【解析】(1)证明::因为 , ,所以, , ,
在直角三角形 中, ,
又因为 , 为 的平分线,
延长 、 交于点 ,连接 ,
在 中, ,所以, 是等腰三角形,
所以,点 是 的中点,
因为直线 平面 ,过 的平面 与平面 的交线为 ,则 ,
因为 是 的中点,所以, 是 的中点.(2)在 中, , , ,则 ,即 ,
由已知得 , ,
又平面 平面 , 平面 ,所以 平面 ,
因为 平面 ,即 ,
所以, 为二面角 的平面角,所以 ,
又 ,所以 为正三角形,
取 的中点为 ,连 ,则 , 平面 ,
以点 为坐标原点, 、 所在直线分别为 、 轴,
平面 内垂直于直线 的直线为 轴建立如下图所示的空间直角坐标系,
则 ,
所以 ,
设 分别为平面 和平面 的法向量,
则 ,取 ,则 ,
,取 ,则 ,
所以 .
则平面 和平面 所成夹角的余弦值为 .
20.(12分)
今年5月以来,世界多个国家报告了猴痘病例,非洲地区猴痘地方性流行国家较多.9月19日,中国疾控
中心发布了我国首例“输入性猴痘病例”的溯源公告.我国作为为人民健康负责任的国家,对可能出现的
猴痘病毒防控已提前做出部署,同时国家卫生健康委员会同国家中医药管理局制定了《猴痘诊疗指南
(2022年版)》.此《指南》中指出:①猴痘病人潜伏期5-21天;②既往接种过天花疫苗者对猴痘病毒
存在一定程度的交叉保护力.据此,援非中国医疗队针对援助的某非洲国家制定了猴痘病毒防控措施之一
是要求与猴痘病毒确诊患者的密切接触者集中医学观察21天.在医学观察期结束后发现密切接触者中未接种过天花疫苗者感染病毒的比例较大.对该国家200个接种与未接种天花疫苗的密切接触者样本医学观察
结束后,统计了感染病毒情况,得到下面的列联表:
接种天花疫苗与否/人数 感染猴痘病毒 未感染猴痘病毒
未接种天花疫苗 30 60
接种天花疫苗 20 90
(1)是否有 的把握认为密切接触者感染猴痘病毒与未接种天花疫苗有关;
(2)以样本中结束医学现察的密切接触者感染猴痘病毒的频率估计概率.现从该国所有结束医学观察的
密切接触者中随机抽取4人进行感染猴痘病毒人数统计,求其中至多有1人感染猴痘病毒的概率:
(3)该国现有一个中风险村庄,当地政府决定对村庄内所有住户进行排查.在排查期间,发现一户3口之
家与确诊患者有过密切接触,这种情况下医护人员要对其家庭成员逐一进行猴痘病毒检测.每名成员进行
检测后即告知结果,若检测结果呈阳性,则该家庭被确定为“感染高危家庭”.假设该家庭每个成员检测
呈阳性的概率均为 且相互独立.记:该家庭至少检测了2名成员才能确定为“感染高危家庭”
的概率为 .求当 为何值时, 最大?附:
0.1 0.05 0.010
2.706 3.841 6.635
【答案】(1)没有 的把握认为密切接触者感染猴痘病毒与未接种天花疫苗有关
(2) ;(3)当 时, 最大
【解析】(1)假设 :密切接触者感染猴痘病毒与未接种天花疫苗无关,
依题意有 ,
故假设不成立, 没有 的把握认为密切接触者感染猴痘病毒与未接种天花疫苗有关.
(2)由题意得,该地区每名密切接触者感染病毒的概率为 ,
设随机抽取的4人中至多有1人感染病毒为事件 ,
则 ,
(3)记事件 为:检测了2名成员确定为“感染高危家庭”;
事件 为:检测了3名成员确定为“感染高危家庭”;
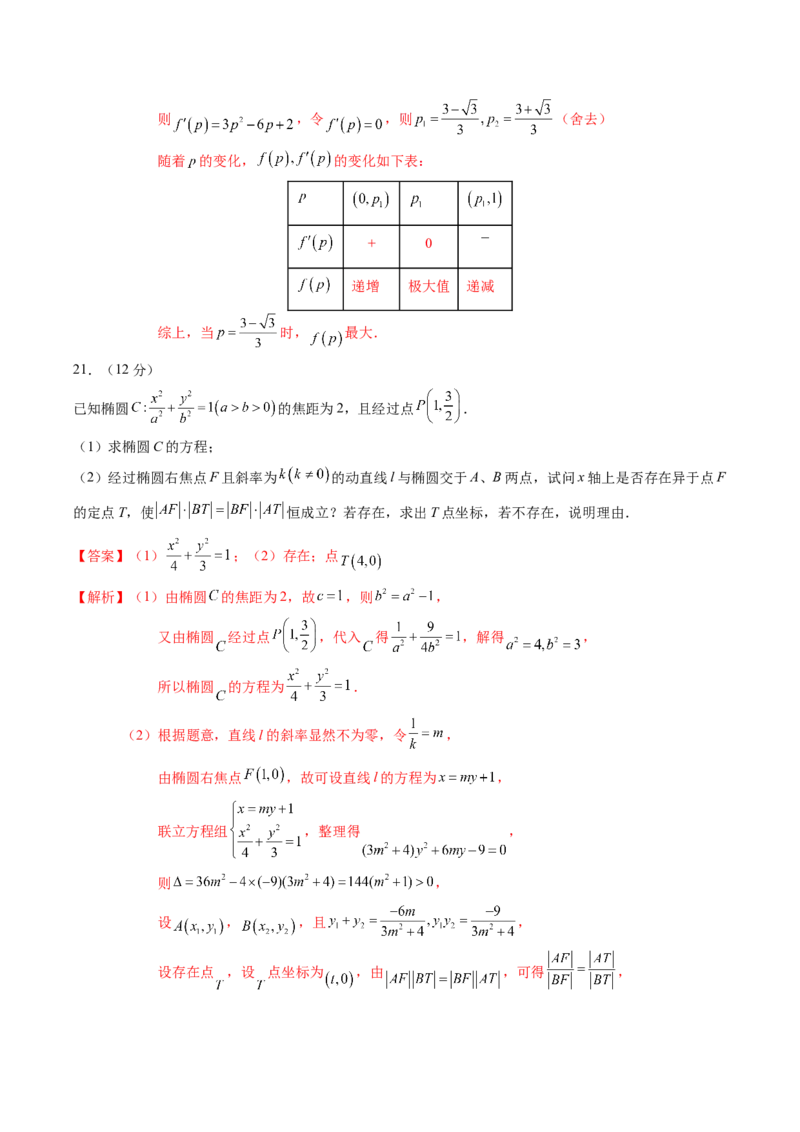
则则 ,令 ,则 (舍去)
随着 的变化, 的变化如下表:
+ 0
递增 极大值 递减
综上,当 时, 最大.
21.(12分)
已知椭圆 的焦距为2,且经过点 .
(1)求椭圆C的方程;
(2)经过椭圆右焦点F且斜率为 的动直线l与椭圆交于A、B两点,试问x轴上是否存在异于点F
的定点T,使 恒成立?若存在,求出T点坐标,若不存在,说明理由.
【答案】(1) ;(2)存在;点
【解析】(1)由椭圆 的焦距为2,故 ,则 ,
又由椭圆 经过点 ,代入 得 ,解得 ,
所以椭圆 的方程为 .
(2)根据题意,直线l的斜率显然不为零,令 ,
由椭圆右焦点 ,故可设直线l的方程为 ,
联立方程组 ,整理得 ,
则 ,
设 , ,且 ,
设存在点 ,设 点坐标为 ,由 ,可得 ,又因为 ,
所以 ,所以 ,
所以直线 和 关于 轴对称,其倾斜角互补,即有 ,
则 ,所以 ,
所以 ,整理得 ,
即 ,即 ,解得 ,
符合题意,即存在点 满足题意.
22.(12分)
已知关于 的方程 有两个不同实根 , .
(1)求实数 的取值范围;
(2)证明: .
【答案】(1) ;(2)证明见解析
【解析】(1)方程 ,
令 , 函数 在 单调递增且 ,
方程 在 有两根 ,
可转化方程 在 有两根 ,其中 ,
令 ,则 在 为减函数,在 为增函数,
又 时, ; 时, , .
(2)不妨设两根 ,则 , ,
令 则 ,
在 单调递增, 时, ,
由 得 , ,
而 在 单调递减,且 ,
所以 ,所以 ,
,,又 ,
,而 在 单调递增,
.