文档内容
【赢在高考·黄金8卷】备战2024年高考数学模拟卷
(新高考Ⅱ卷专用)
黄金卷01
(考试时间:120分钟 试卷满分:150分)
第 I 卷(选择题)
一、单项选择题:本题共8小题,每小题5分,共40分,在每小题给出的四个选项中,只有一项是符合要
求的。
1.设集合 , ,且 ,则 ( )
A.6 B.4 C. D.
【答案】D
【解析】 , ,
∵ ,∴ ,∴ ,
故选:D.
2.已知 ,则 ( ).
A. B. C.2 D.1
【答案】C
【解析】由 ,得 ,
则 ,所以 .
故选:C.
3.已知 的图象与直线 在区间 上存在两个交点,则当 最大时,曲线
的对称轴为( )A. , B. ,
C. , D. ,
【答案】D
【解析】当 时 ,
要使得 的图象与直线 存在两个交点,
则 ,解得 ,
又因为 ,所以 ,所以 ,
此时曲线 的对称轴为 , ,
解得 , ,
故选:D
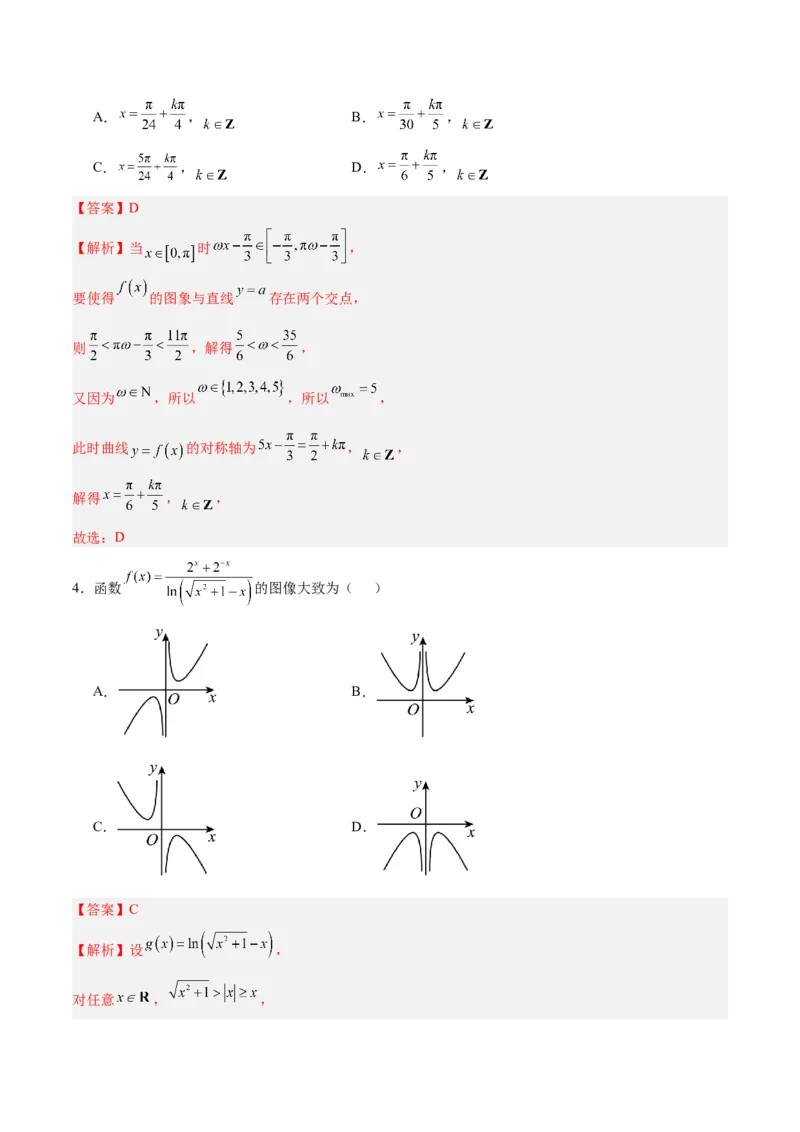
4.函数 的图像大致为( )
A. B.
C. D.
【答案】C
【解析】设 ,
对任意 , ,所以 ,
所以 的定义域为 ,
,
所以函数 为奇函数.
令 ,
可得 ,即 ,
所以 ,可得 ,
由 可得 ,解得 ,
所以 的定义域为 ,
又 ,
所以函数 为奇函数,排除BD选项,
当 时, 是减函数,
则 , ,
所以 ,排除A选项.
故选:C
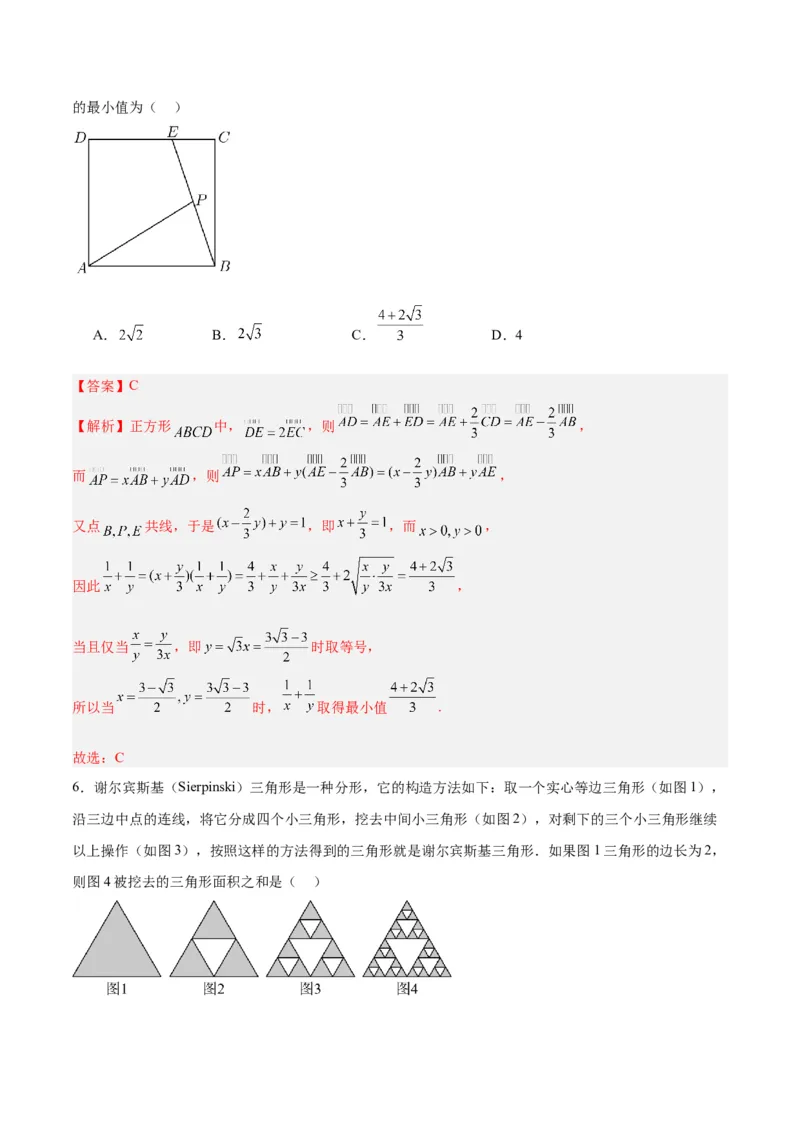
5.如图,正方形 中, 是线段 上的动点,且 ,则的最小值为( )
A. B. C. D.4
【答案】C
【解析】正方形 中, ,则 ,
而 ,则 ,
又点 共线,于是 ,即 ,而 ,
因此 ,
当且仅当 ,即 时取等号,
所以当 时, 取得最小值 .
故选:C
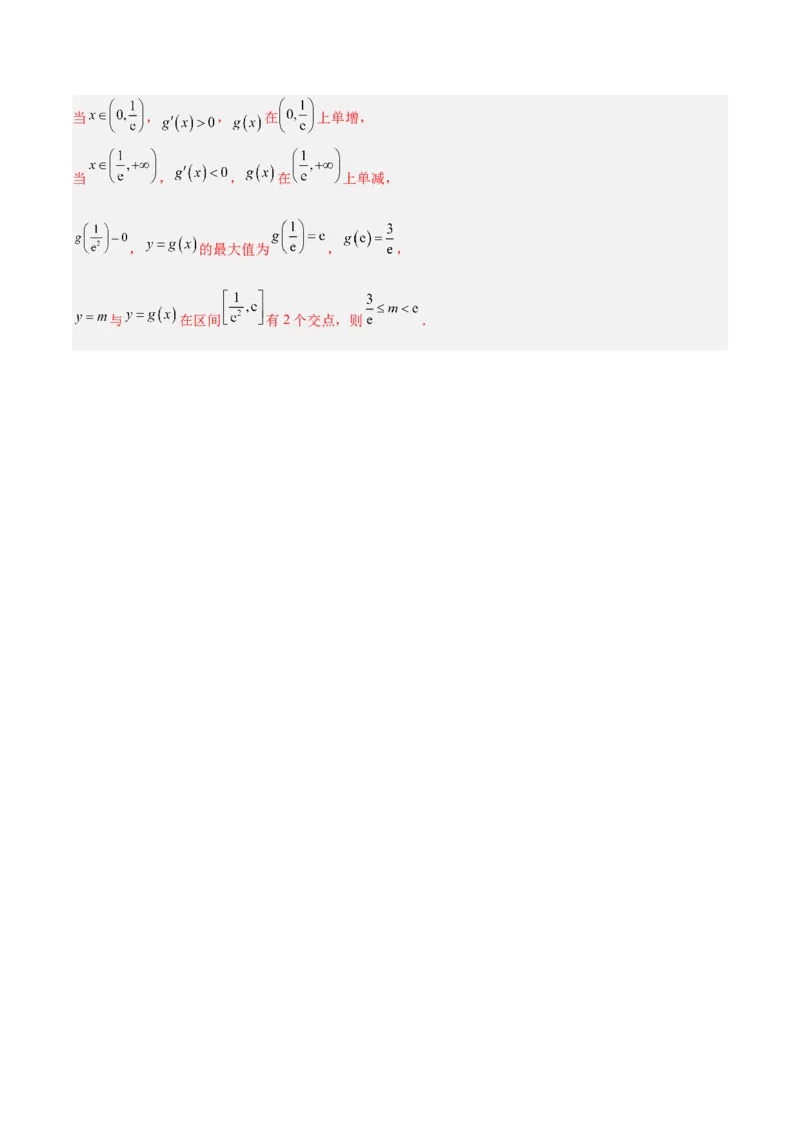
6.谢尔宾斯基(Sierpinski)三角形是一种分形,它的构造方法如下:取一个实心等边三角形(如图1),
沿三边中点的连线,将它分成四个小三角形,挖去中间小三角形(如图2),对剩下的三个小三角形继续
以上操作(如图3),按照这样的方法得到的三角形就是谢尔宾斯基三角形.如果图1三角形的边长为2,
则图4被挖去的三角形面积之和是( )A. B. C. D.
【答案】D
【解析】第一种挖掉的三角形边长为 ,共 个,面积为 ;
第二种挖掉的三角形边长为 ,共 个,面积为 ,
第三种挖掉的三角形边长为 ,共 个,
面积为 ,
故被挖去的三角形面积之和是 .
故选:D
7.已知函数 满足对于任意实数 ,都有 成立,则实数 的
取值范围是( )
A. B. C. D.
【答案】D
【解析】依题意,对于任意实数 ,都有 成立,
不妨设 ,则 ,
所以 在 上单调递减,所以 ,解得 .
故选:D
8.已知双曲线 右支上非顶点的一点A关于原点的对称点为 为双曲线的右焦点,若
,设 ,且 ,则该双曲线的离心率的取值范围为( )
A. B. C. D.
【答案】C
【解析】如图所示,设双曲线的左焦点为 ,连接 , ,
因为 ,则四边形 为矩形,
所以 ,
则 , .
.
.
即 ,
则 ,
因为 ,则 ,可得 ,即 ,
所以 ,
即双曲线离心率的取值范围是 ,
故选:C.
二、多项选择题:本题共4小题,每小题5分,共20分,在每小题给出的四个选项中,有多项符合题目的
要求,全部选对的得5分,部分选对的得2分,有选错的得0分。
9.已知圆M: ,则下列关于圆M的结论正确的是( )
A.点 在圆M内
B.圆M关于直线 对称
C.圆M与圆O: 相切
D.若直线l过点 ,且被圆M截得的弦长为 ,则l的方程为
【答案】BC
【解析】圆 的方程为 ,即圆心为 ,半径为 ,
对于A:因为 ,所以点 在圆 外,故选项A错误;
对于B:因为 ,所以圆心在直线上,故选项B正确;
对于C:因为圆O、圆 的圆心距为 ,两圆的半径差为 ,
所以两圆内切,故选项C正确;
对于D:当直线l的斜率不存在时,其方程为 ,圆心 到直线l的距离为 ,
直线被圆所截得的弦长为 ,
当直线l的斜率存在时,设其方程为 ,圆心 到直线l的距离为 ,解得 ,可得直线l的方程为 ,综上所述,直线l的方程为 或 ,故选
项D错误.
故选:BC.
10.下列说法正确的是( )
A.若数据 的方差为1,则新数据 , ,…, 的方差为1
B.已知随机事件A和B互斥,且 , ,则 等于0.5.
C.“ ”是直线 与直线 互相垂直的充要条件
D.无论实数λ取何值,直线 恒过定点
【答案】ABD
【解析】对于A:若数据 的方差为1,则新数据 , ,…, 的稳定程度没有发生
改变,方差还是 ,A正确;
对于B:随机事件A和B互斥,且 , ,
则 ,
则 ,B正确;
对于C:若直线 与直线 互相垂直,则 ,
解得 或 ,
故“ ”是直线 与直线 互相垂直的充分不必要条件,C错误;
对于D:直线
即为 ,令 ,解得 ,
即无论实数λ取何值,直线 恒过定点 ,D正确.
故选:ABD.11.如图,在棱长为2的正方体 中, , 分别是棱 , 的中点,点 在 上,
点 在 上,且 ,点 在线段 上运动,下列说法正确的有( )
A.当点 是 中点时,直线 平面 ;
B.直线 到平面 的距离是 ;
C.存在点 ,使得 ;
D. 面积的最小值是
【答案】AC
【解析】对于A,由 是 中点, ,得点 是 的中点,连接 ,显然 也是 的中点,
连接 ,
于是 ,而 平面 , 平面 ,所以直线 平面 ,A正确;对于B, 分别是棱 的中点,则 , 平面 , 平面 ,于是
平面 ,
因此直线 到平面 的距离等于点 到平面 的距离h,
,
, , ,
由 ,得 ,B错误;
以A为原点,建立如图所示空间直角坐标系,则 , , , ,
对于C,设 ,则 , , ,
,
由 ,得 ,解得 ,
由于 ,因此存在点 ,使得 ,C正确;
对于D,由选项C得 在 的投影点为 ,则P到 的距离 ,
面积为 ,所以当 时, 取得最小值为 ,D错误.
故选:AC
12.已知 、 都是定义在 上的函数,且 为奇函数, 的图像关于直线 对称,则下
列说法中一定正确的是( )
A. B.
C. 为奇函数 D. 的图像关于直线 对称
【答案】AD
【解析】解:因为 是定义在 上的函数,且 为奇函数,所以 ,故A正确;
因为 是定义在 上的函数,且 的图像关于直线 对称,所以 , 不一定
为0,故B错误;C明显错误;
因为 ,所以 的图像关于直线 对称,故D正确.
故选:AD
第 II 卷(非选择题)
三、填空题:本题共4小题,每小题5分,共20分。
13.已知 的展开式中各项系数的和为 ,则实数 的值为 .
【答案】
【解析】因为 的展开式中各项系数的和为 ,
令 ,可得 ,解得 .
故答案为: .14.已知等差数列 的前 项和分别为 ,且 ,则 .
【答案】
【解析】等差数列 的前 项和分别为 ,且 ,
所以 .
故答案为:
15.在 中,角 , , 所对的边分别为 , , ,已知 , , ,则
的最大值为 .
【答案】 /
【解析】由题意,
, 所以消去 得
,
由 , 得 ,当且仅当 时等号成立,
∴ ,∴原式
故答案为: .
16.在棱长为2的正方体 中,点M是对角线 上的点(点M与A、 不重合),则下
列结论正确的是 .(请填写序号)
①存在点M,使得平面 平面 ;
②存在点M,使得 平面 ;
③若 的面积为S,则 ;
④若 、 分别是 在平面 与平面 的正投影的面积,则存在点M,使得 .
【答案】①②④
【解析】连接 , ,
①设平面 与对角线 交于M,
由 , ,且 平面 , 平面 ,且 ,
所以 平面 ,即 平面 ,
所以存在点M,使得平面 平面 ,所以①正确;
②连接 , ,
由 , 平面 , 平面 ,
所以 平面 ,同理由 可得 平面 ,
又 , 平面 , 平面 ,
所以平面 平面 ,
设平面 与 交于点M,则 平面 ,
所以 平面 ,所以②正确;
③连接 交 于点O,过O点作 ,在正方体 中,
由① 平面 ,同理可证 平面 ,
且 平面 ,
所以 ,所以OM为异面直线 与 的公垂线,
根据 ,所以 ,
即 ,
此时 的面积为 ,
所以③不正确;
④设点 在平面 的正投影为 ,在平面 的正投影为
如图,因为 平面 ,
则 在平面 内的射影为 ,
由 ,则 ,
故在点 从 的中点向着点A运动的过程中,
点 也从 的中点向着点 运动.由 平面 ,则 ,
故当 为 中点时, 正投影 也为 中点,
此时 在平面 的正投影的面积 ,
因此,在点 从 的中点向着点A运动的过程中,
的面积即 从1减少到趋向于0,即 ,
同理,在点 从 的中点向着点A运动的过程中,
点 也从 的中点向着点 运动, 的面积即 从0开始增加,
当 与 重合时, 正投影 与 重合,
此时 在平面 的正投影的面积 ,
所以 ,
故在此过程中,必存在某个点 使得 ,所以④正确,
故答案为:①②④.
四、解答题:本题共6小题,共70分,解答应写出必要的文字说明、证明过程及验算步骤。
17.(10分)已知点 是角 终边上一点.
(1)求 的值;
(2)若将角 终边绕着坐标原点逆时针旋转 得到角 的终边,求 的值.
【答案】(1)
(2)【解析】(1)因为点 是角 终边上一点,
所以 , , ,
(2)将角 终边绕着坐标原点逆时针旋转 得到角 的终边,
故 ,
所以
18.(12分)已知正项数列 的前 项和 ,满足: .
(1)求数列 的通项公式;
(2)记 ,设数列 的前 项和为 ,求证 .
【答案】(1)
【解析】(1)当 时, ,解得 .
当 时,由 ①,可得 ,②
① ②得: ,即 .
,
.是以1为首项,以2为公差的等差数列,
数列 的通项公式 .
(2)由(1)可得 ,
,
, , , , ,
,
.
19.(12分)如图,在四棱柱 中,四棱锥 是正四棱锥, .
(1)求 与平面 所成角的正弦值;
(2)若四棱柱 的体积为16,点 在棱 上,且 ,求点 到平面 的距离.
【答案】(1)
(2)【解析】(1)因为四棱锥 是正四棱锥,连接 交于点 ,则 ,
连接 ,则 平面 ,所以 两两垂直.
如图所示,以点 为坐标原点, 所在直线分别为 轴, 轴, 轴,建立空间直角坐标系
,
设 ,因为 , ,则 ,
设 与 交于点 ,则 为 的中点,
所以 ,
,
所以 ,设平面 的一个法向量为 ,则有 ,
得 ,
取 ,得 ,
直线 的一个方向向量为 ,
设 与平面 所成角为 ,则 ,
所以直线 与平面 所成角的正弦值为 .
(2)因为四棱柱 的体积为 ,所以 ,
由(1)知, ,
.
因为 ,则 ,
所以 ,
,
设平面 的一个法向量为 ,则有 ,得 ,
取 ,得 ,
所以点 到平面 的距离为 .
20.(12分)第19届亚运会于9月23日至10月8日在杭州举行,某学校为持续营造全民参与亚运、服务
亚运、奉献亚运的浓厚氛围举办“心心相融·爱答亚运”知识挑战赛.挑战者向守擂者提出挑战,规则为挑
战者和守擂者轮流答题,直至一方答不出或答错,则另一方自动获胜.若赛制要求挑战者先答题,守擂者
和挑战者每次答对问题的概率都是 ,且每次答题互不影响.
(1)若在不多于两次答题就决出胜负,则挑战者获胜的概率是多少?
(2)在此次比赛中,挑战者获胜的概率是多少?
(3)现赛制改革,挑战者需要按上述方式连续挑战8位守擂者,每次挑战之间相互独立,当战胜至少三分之
二以上的守擂者时,则称该挑战者胜利.若再增加1位守擂者时,试分析该挑战者胜利的概率是否增加?并
说明理由.【答案】(1)0.25
(2)
(3)没有增加,理由见解析
【解析】(1)设事件 为挑战者获胜,事件 为不多于两次答题比赛结束.
.
(2)设 为先答题者获胜的概率,则 ,解得 ,
所以挑战者获胜的概率是 .
(3)设随机变量 为挑战者连续挑战8人时战胜得守擂者人数, 为此时挑战者获胜的概率;
为挑战者连续挑战9人时战胜得守擂者人数, 为此时挑战者获胜的概率.
,
,
显然, ,即该挑战者胜利的概率没有增加.
21.(12分)已知椭圆 : ,点 、 分别是椭圆 的左焦点、左顶
点,过点 的直线 (不与x轴重合)交椭圆 于A,B两点.
(1)求椭圆M的标准方程;(2)若 ,求 的面积;
(3)是否存在直线 ,使得点B在以线段 为直径的圆上,若存在,求出直线 的方程;若不存在,请说明
理由.
【答案】(1)
(2)
(3)不存在,理由见详解
【解析】(1)由左焦点 、左顶点 可知: ,则 ,
所以椭圆 的标准方程为 .
(2)因为 , ,
则过 的直线 的方程为: ,即 ,
解方程组 ,解得 或 ,
所以 的面积 .
(3)若点B在以线段 为直径的圆上,等价于 ,即 ,
设 ,则 ,
因为 ,则 ,
令 ,
解得: 或 ,又因为 ,则不存在点 ,使得 ,
所以不存在直线 ,点B在以线段 为直径的圆上.
22.(12分)已知函数 .
(1)求 的极值;
(2)若 在区间 有2个零点,求 的取值范围.
【答案】(1)当 时, 在 处取极大值
(2)
【解析】(1)因为 ,定义域为 ,所以 ,
当 时,由于 ,则 恒成立,
所以 在 上单调递增, 无极值,
当 时,令 ,解得 ,
当 时, ,则 在 上单调递增;
当 时, ,则 在 上单调递减:
所以当 时, 在 处取极大值 ,无极小值;
(2) ,
令 ,得 ,令 , 在区间 有2个零点,
即 与 在区间 有2个交点,
, , ,当 , , 在 上单增,
当 , , 在 上单减,
, 的最大值为 , ,
与 在区间 有2个交点,则 .