2024届石家庄市高中毕业年级教学质量检测三物理参考答案（终）_2024年5月_01按日期_13号_2024届河北省石家庄市高三教学质量检测（三）

石家庄市 2024 届高中毕业年级教学质量检测（三） 物理参考答案 一、单项选择题：本题共7小题，每小题4分，共28分。在每小题给出的四个选项中，只 有一项符合题目要求。 1 2 3 4 5 6 7 B D C D A B B 二、多项选择题：本题共3小题，每小题6分，共18分。在每小题给出的四个选项中，有 两个或两个以上选项符合题目要求。全部选对的得6分，选对但不全的得3分，有选错的得 0分。 8 9 10 BC AD ABC 三、非选择题：共54分。 11.（8分） （1）③ （2分） （2）V （2分） n （2分）（3）装置出现漏气或环境温度降低 （写出 一个原因即可，2分） 12.（8分） （I -I）R （1）C（写R 给分，2分）（2）如图所示（连线有错误均不给分，2分）（3） 2 1 1 （角 1 I 1 标有错误均不给分，2分）（4）122~162（2分） 13. （8分） （1）（3分）由图甲乙可看出，该波的波长、周期分别为： 8m,T 4s（2分）  则波速：v 2m/s （1分） T （2）（5分）由题意可知，t 0时刻，y10m的质点起振，且起振方向向上，波传至B点 1 1 {#{QQABIYoAoggIAIIAARgCEwEgCkCQkBGCCIoGhFAMMAIACRFABAA=}#}1610 需要的时间为：Δt   3s（1分） 1 v 13 质点B振动的时间为：Δt t Δt  s（1分） 2 2 1 3   质点B的振动方程为：z Asint  Asin Δt （1分）  2 2 由图乙知，该波中质点的振幅A10cm，质点B相对于平衡位置的位移 1  z 10sin   5cm（2分） 6  （其他解法正确均给分） 14. （14分） （1）A向右运动，由牛顿第二定律得： （1分） = 由运动学公式：2al v2（1分） 1 0 设A、B碰后瞬间，A的速度为v ，B的速度为v ，由动量守恒定律得 1 2 mv mv Mv （1分） 0 1 2 由机械能守恒定律得 1 1 1 mv2  mv2 Mv2（1分） 2 0 2 1 2 2 联立解得：v 1m/s，v 2m/s（1分） 1 2 （2）A，B碰后，B向右做匀减速运动，A向左减速，对B，由牛顿第二定律 Mg a （1分） M 设B经时间t向右运动x距离停止，有 2ax0v2（1分） 2 0v at（1分） 2 联立解得：x0.4m，t0.4s t时间内，设A位移为s对A，有 1 svt at2（1分） 1 2 此时，A的速度为 vv at （1分） 1 联立解得：x0.4m，v3m/s 即B停止的瞬间，A刚好与B相碰，再次重复第一次的碰撞。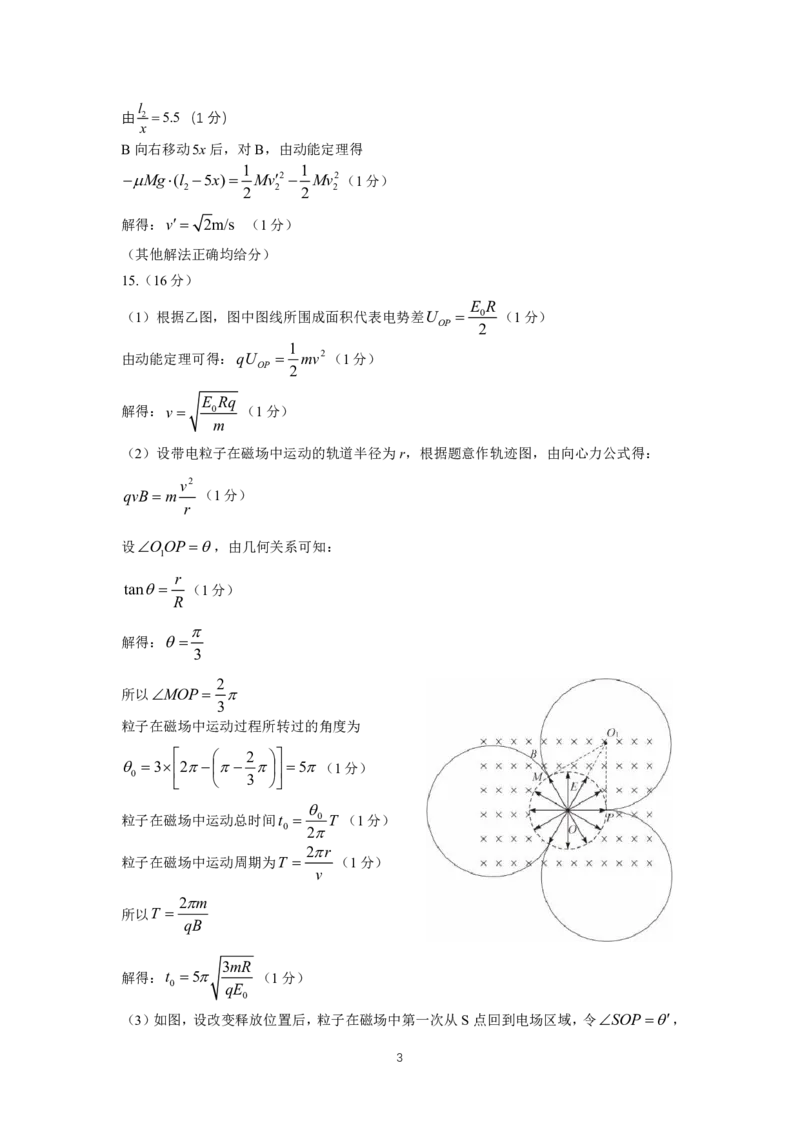 则A、B第一次碰后瞬间到第二次碰前瞬间的时间间隔t0.4s（1分） （3）A、B每经历一次碰撞，B向右移动x0.4m 2 {#{QQABIYoAoggIAIIAARgCEwEgCkCQkBGCCIoGhFAMMAIACRFABAA=}#}l 由 2 5.5（1分） x B向右移动5x后，对B，由动能定理得 1 1 Mg(l 5x) Mv2  Mv2（1分） 2 2 2 2 2 解得：v 2m/s （1分） （其他解法正确均给分） 15.（16分） E R （1）根据乙图，图中图线所围成面积代表电势差U  0 （1分） OP 2 1 由动能定理可得：qU  mv2（1分） OP 2 E Rq 解得：v  0 （1分） m （2）设带电粒子在磁场中运动的轨道半径为r，根据题意作轨迹图，由向心力公式得： v2 qvB m （1分） r 设OOP，由几何关系可知： 1 r tan （1分） R  解得： 3 2 所以MOP  3 粒子在磁场中运动过程所转过的角度为   2   3 2  5（1分） 0   3   粒子在磁场中运动总时间t  0 T （1分） 0 2 2r 粒子在磁场中运动周期为T  （1分） v 2m 所以T  qB 3mR 解得：t 5 （1分） 0 qE 0 （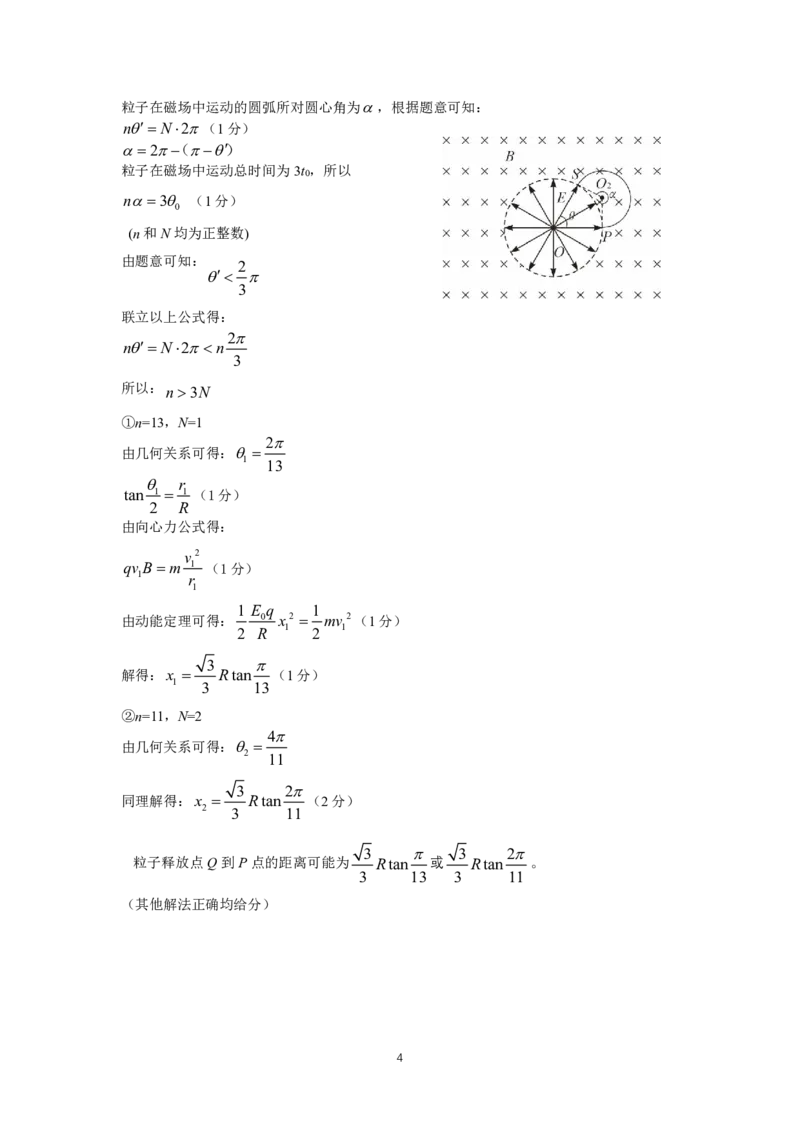3）如图，设改变释放位置后，粒子在磁场中第一次从S点回到电场区域，令SOP ， 3 {#{QQABIYoAoggIAIIAARgCEwEgCkCQkBGCCIoGhFAMMAIACRFABAA=}#}粒子在磁场中运动的圆弧所对圆心角为，根据题意可知： n N2（1分） 2（） 粒子在磁场中运动总时间为3t ，所以 0 n3 （1分） 0 (n和N均为正整数) 由题意可知： 2   3 联立以上公式得： 2 n N2n 3 所以： n3N ①n=13，N=1 2 由几何关系可得：  1 13  r tan 1  1 （1分） 2 R 由向心力公式得： v2 qv B m 1 （1分） 1 r 1 1 E q 1 由动能定理可得： 0 x2  mv2（1分） 2 R 1 2 1 3  解得：x  Rtan （1分） 1 3 13 ②n=11，N=2 4 由几何关系可得：  2 11 3 2 同理解得：x  Rtan （2分） 2 3 11 3  3 2 粒子释放点Q到P点的距离可能为 Rtan 或 Rtan 。 3 13 3 11 （其他解法正确均给分） 4 {#{QQABIYoAoggIAIIAARgCEwEgCkCQkBGCCIoGhFAMMAIACRFABAA=}#}