文档内容
【赢在高考·黄金8卷】备战2024年高考数学模拟卷(全国卷专用)
黄金卷01
(考试时间:120分钟 试卷满分:150分)
第 I 卷(选择题)
一、选择题:本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题
目要求的.
1 2 3 4 5 6 7 8 9 10 11 12
C D B A C C D B A A B B
第 II 卷(非选择题)
二、填空题:本大题共4小题,每小题5分,共20分
13. 14.1 15. 16.①③④
三、解答题:本大题共70分.解答应写出文字说明、证明过程或演算步骤.第17~21题为必考题,每个试
题考生都必须作答.第22、23题为选考题,考生根据要求作答.
(一)必考题:共60分.
17.【答案】(1)有 以上的把握认为倾向“坐标系与参数方程”还是“不等式选讲”与性别有关
(2)分布列见解析,
【详解】(1)依题意得 列联表:
倾向“坐标系与参数方 倾向“不等式选
合计
程” 讲”
男
15 25 40
生
女
20 10 30
生
合
35 35 70
计
所以 ,(4分)
所以有 以上的把握认为倾向“坐标系与参数方程”还是“不等式选讲”与性别有关.(6分)(2)在倾向“坐标系与参数方程”的学生中,女生与男生的人数的比值为 ,所以在倾向“坐
标系与参数方程”的学生抽取的7人中男生有3人.
所以 的取值为 ,
则 .(9分)
故 的分布列为:
0 1 2 3
所以 .(12分)
18.【答案】(1) (2)
【详解】(1)由 , ,
当 时, ,
两式相减得 ,即 ,
所以数列 为等比数列,公比为 .(3分)
选①,由 , , 成等差数列,
可得 ,即 ,
解得 ,所以 .(6分)
选②,由 , , 成等比数列,
得 ,即 ,解得 ,所以 .(6分)
选③,由 ,得 ,
所以 .(6分)
(2)当 为奇数时, ,
记前 项和 中的奇数项之和为 ,
则 .(9分)
当 为偶数时, ,
记前 项和 中的偶数项之和为 ,
则 ,
故 .(12分)
19.【答案】(1)证明见解析(2)
【详解】(1)证明:因为 平面 , 平面 ,所以 ,
因为 ,四边形 是平行四边形,所以四边形 是菱形,所以 .(2分)
又因为 , 平面 , 平面 ,
所以 平面 ,
因为 平面 ,
所以 .(5分)
(2)解:以 为原点,分别以 , , 所在直线为 , , 轴建立如图所示的空间直角坐标系,
如图所示,则 , , , ,
所以 , , ,
设平面 的一个法向量为 ,
则 ,取 ,可得 , ,
所以 ,
设平面 的一个法向量为 ,
则 ,取 ,可得 , ,
所以 ,(9分)设二面角 的大小为 ,
因为 ,
所以 ,
所以二面角 的正弦值为 .(12分)
20.【答案】(1) (2)是定值,理由见解析
【详解】(1)由题意得 ,解得 ,所以椭圆 的方程为 .(3分)
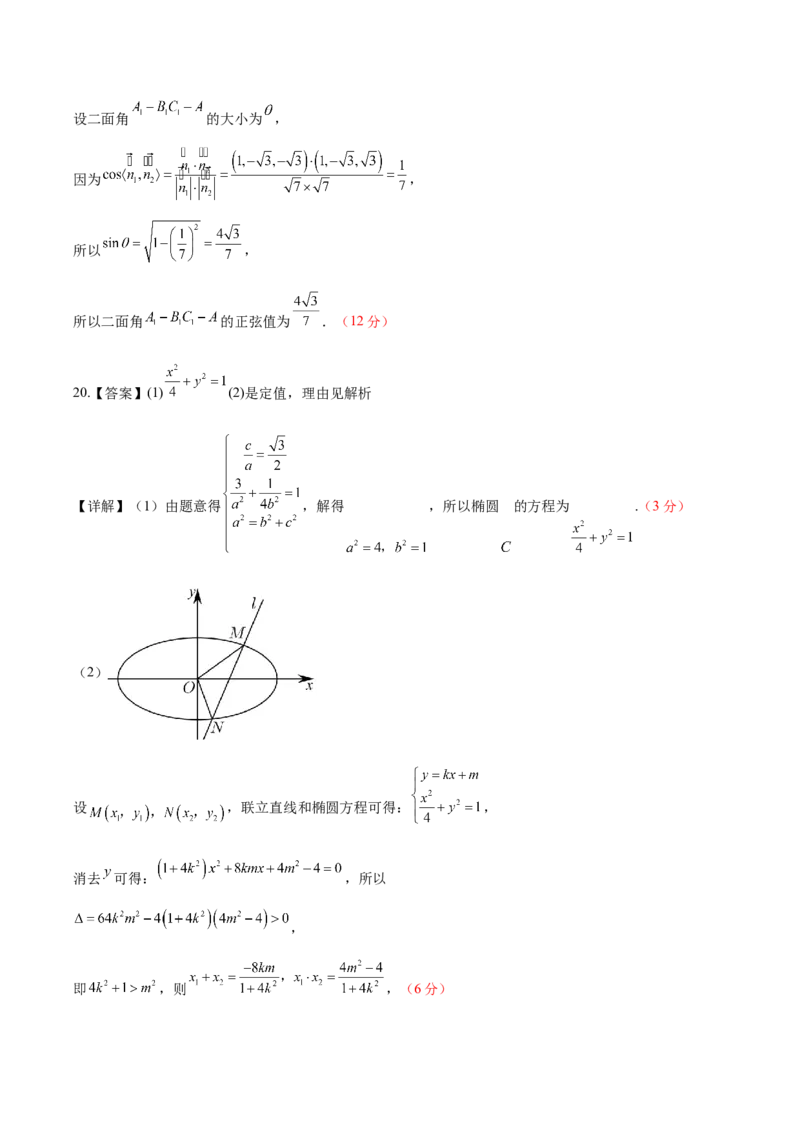
(2)
设 ,联立直线和椭圆方程可得: ,
消去 可得: ,所以
,
即 ,则 ,(6分), ,
把韦达定理代入可得: ,
整理得 ,(9分)
又 ,
而 点到直线 的距离 ,
所以 ,
把 代入,则 ,可得 是定值1.(12分)
21.【答案】(1) (2) .
【详解】(1)由 ,
则 ,
所以 ,即切线斜率为 ,
又 ,则切点为 .
切线方程为 ,
所以曲线 在点 处的切线方程为 .(3分)
(2)根据题意得, ,则 .
由0为 的极小值点,可知 .
设 ,
则 .(5分)
(ⅰ)当 时, ,
所以 在 上单调递增,又 ,
所以当 时, , 单调递减;
当 时, , 单调递增,
所以0是 的极小值点,符合题意.(7分)
(ⅱ)当 时,设 ,
则 ,
所以 在 上单调递增, ,
,
所以存在 ,使得 ,
所以当 时, , 单调递减,即 单调递减;
当 时, , 单调递增,即 单调递增.又 ,
所以当 时, , 单调递减;
当 时, , 单调递增,
所以0是 的极小值点,符合题意.(9分)
(ⅲ)当 时, ,且 在 上单调递增,
所以当 时, , 单调递减,即 单调递减;
当 时, , 单调递增,即 单调递增.
又 ,所以 , 单调递增,不符合题意.
(ⅳ)当 时, , 在 上单调递增, ,
所以存在 ,使得 ,
所以当 时, , 单调递减,又 ,
所以当 时, , 单调递增;
当 时, , 单调递减.
所以0是 的极大值点,不符合题意.
综上, 的取值范围是 .(12分)
(二)选考题:共10分.请考生在22、23题中任选一题作答,如果多做,则按所做的第一题计分.
选修4-4:坐标系与参数方程
22.【答案】(1) ; (2)【详解】(1)因为曲线 的参数方程为 (t为参数),
则 , ,
两式相减,得 的普通方程为: ;
曲线 的参数方程为 ( 为参数),
所以 的普通方程为: .(5分)
(2)因为 ,
所以曲线 的极坐标方程为 ,即 ,
联立 ,得 ,
所以射线 与曲线 交于A ,(7分)
而 的普通方程 ,可化为 ,
所以曲线 的极坐标方程为 ,即 ,
联立 ,得 ,
所以射线 与曲线 交于B ,
又点 ,所以 ,
则 .(10分)选修4-5:不等式选讲
23.【答案】(1) ;(2)1
【详解】(1)由已知不等式 为 ,
时,不等式为 , ,所以 ;
时,不等式为 , ,不成立;
时,不等式为 , ,所以 ,
综上,不等式的解集为 ;(5分)
(2) ,即 的最小值是 ,
所以 ,又 ,所以 ,
所以 ,当且仅当 时等号成立.
所以所求最小值为1. (10分)