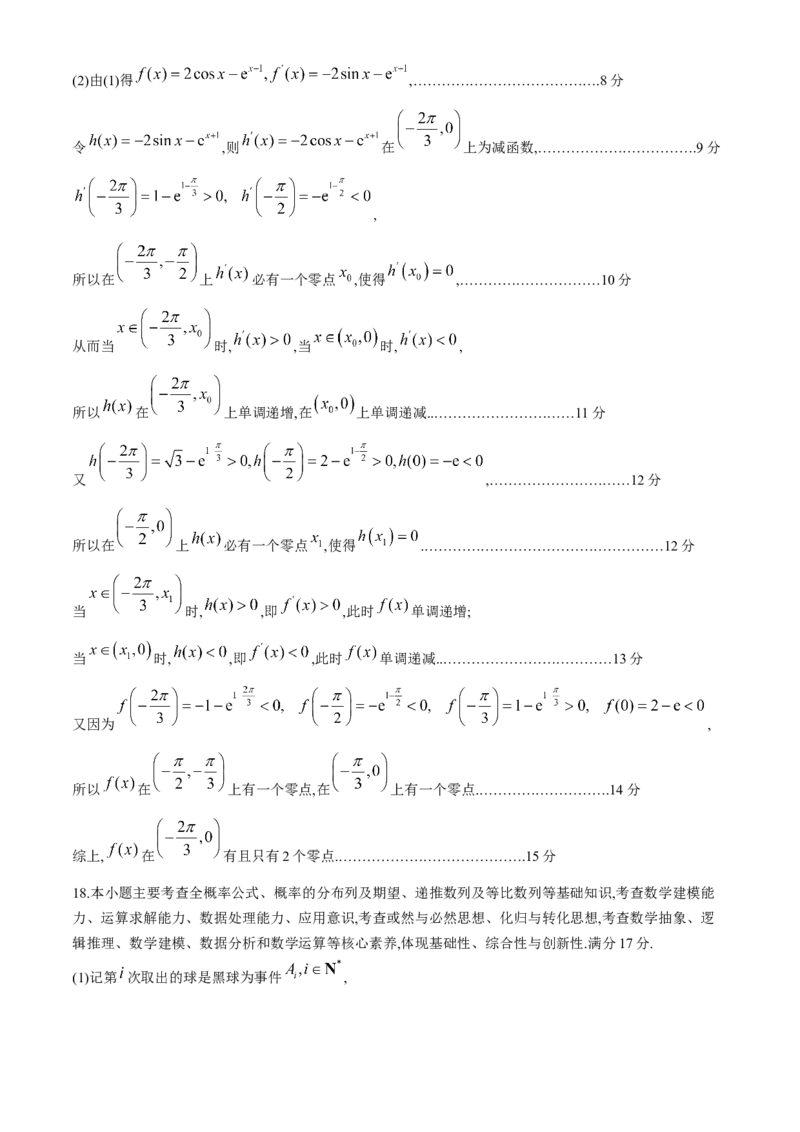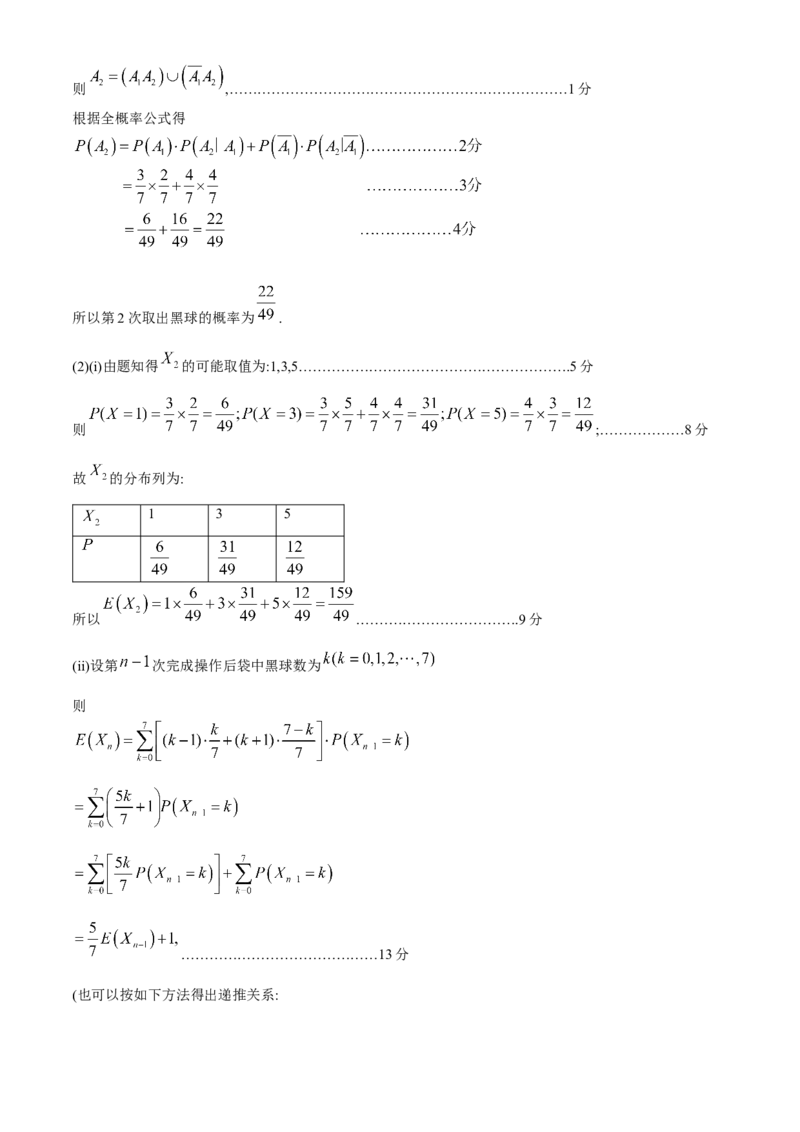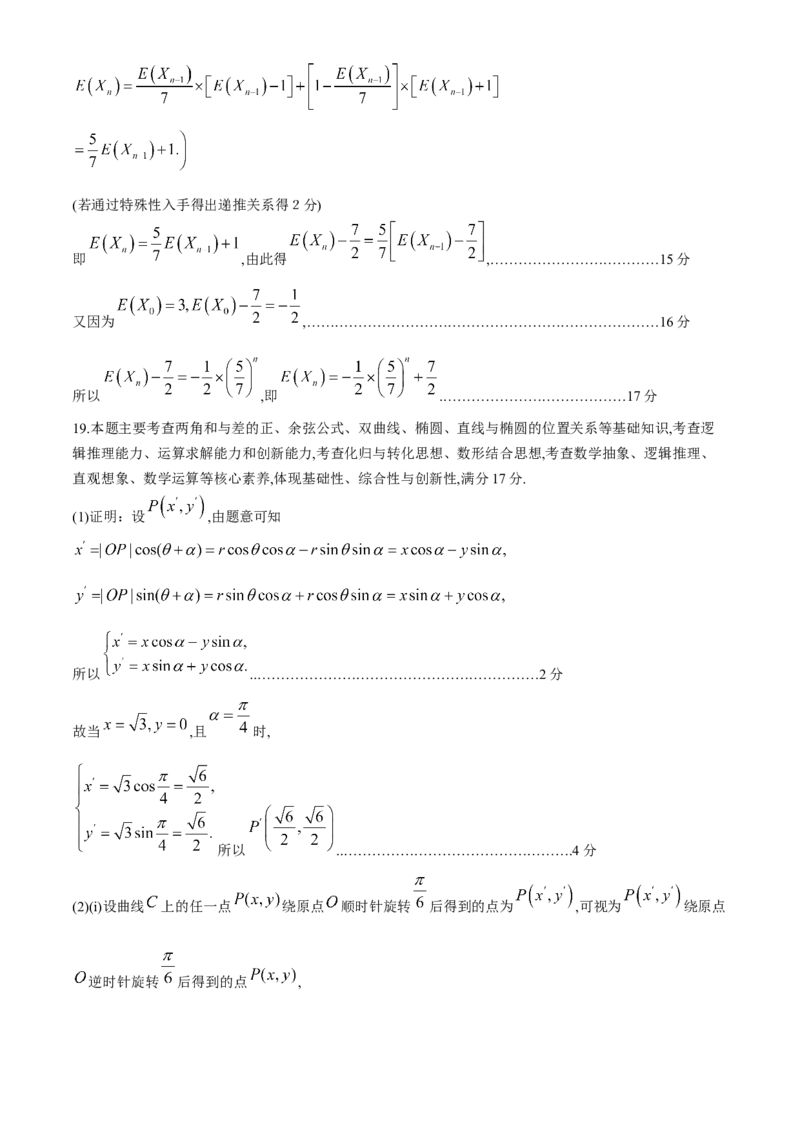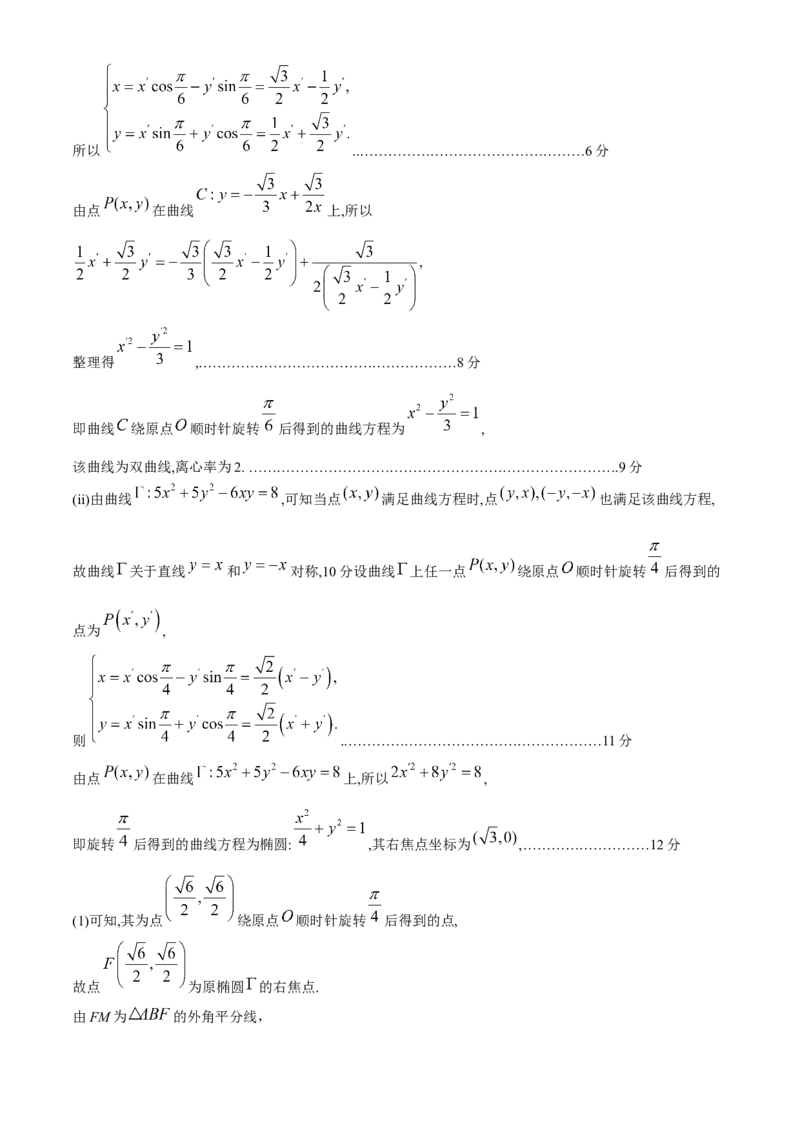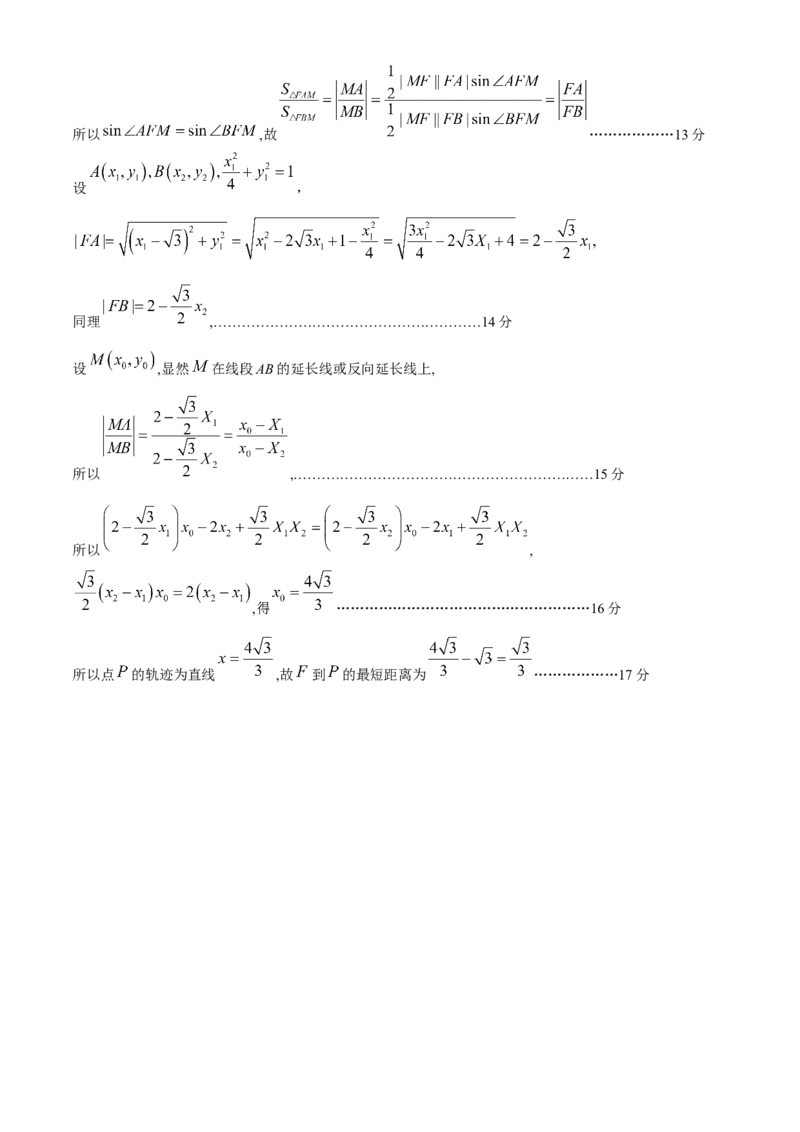文档内容
2024 届福建省宁德市普通高中毕业班五月质量检测数学试题
注意事项:
1.答题前,学生务必在练习卷、答题卡规定的地方填写自己的学校、准考证号、姓名。学生要
认真核对答题卡上粘贴的条形码的“准考证号、姓名”与学生本人准考证号、姓名是否一致。
2.回答选择题时,选出每小题答案后,用2B铅笔把答题卡上对应题目的答案标号涂黑。如需改
动,用橡皮擦干净后,再选涂其他答案标号。回答非选择题时,将答案写在答题卡上。写在本练
习卷上无效。
3.答题结束后,学生必须将练习卷和答题卡一并交回。
一、选择题:本题共8小题,每题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目
要求的.
1.样本数据2,2,3,3,3,4,4,5,5,6的中位数和众数分别为
A.3和3 B.3.5和3 C.4和3 D.3.5和2,3,4,5
2.已知集合 .若 ,则 的取值范围是
A. B. C. D.
3.设 表示两条不同的直线, 表示平面,则以下结论正确的是
A.若 ,则 B.若 ,则
C.若 ,则 D.若 ,则
4.记 为等比数列 的前 项积.设命题 命题 ,则 是 的
A.充分不必要条件 B.必要不充分条件
C.充要条件 D.既不充分也不必要条件
5. 2024海峓两岸各民族欢度“三月三”暨福籽同心爱中华 福建省第十一届“三月三”畲族文化节活动在
宁德隆重开幕.海峡两岸各民族同胞齐聚于此,与当地群众共同欢庆“三月三”,畅叙两岸情.在活动现场,为了
解不同时段的入口游客人流量,从上午10点开始第一次向指挥中心反馈入口人流量,以后每过一个小时反馈
一次.指挥中心统计了前5次的数据 ,其中 为第 次入口人流量数据(单位:百人),由此
得到 关于 的回归方程 .已知 ,根据回归方程(参考数据:
),可顶测下午4点时入口游客的人流量为
A.9.6 B.11.0 C.11.4 D.12.0
6.已知圆台 的上底半径为3,下底半径为6,母线长为6,则以下结论错误的是
A.圆台侧面积为 B.圆台外接球的半径为6
学科网(北京)股份有限公司C.圆台的体积为 D.圆台侧面上的点到下底圆心 的最短距离为
7.已知抛物线 的焦点为 是抛物线上的两个动点.若 ,
则 的最大值为
A. B. C. D.
8.函数 ,若关于 的不等式 有且仅有三个整数解,则 的取值范围是
A. B. C. D.
二、选择题:本题共3小题,每小题6分,共18分.在每小题给出的选项中,有多项符合题目要求.
全部选对的得6分,部分选对的得部分分,有选错的得0分.
9.已知 是两个复数,下列结论中正确的是
A.若 ,则 B.若 为实数,则
C.若 均为纯虚数,则 为实数 D.若 为实数,则 均为纯虚数
10.函数 .若存在 ,使得 为奇函数,则实数 的值可以是
A. B. C. D.
11.若定义在 上的函数 满足 ,且值域为 ,则以下结论正确
的是
A. B. C. 为偶函数 D. 的图象关于 中心对称
三、填空题:本题共3小题,每小题5分,共15分.
12.已知 是两个单位向量,若 在 上的投影向量为 ,则 与 的夹角为______________.
13.中国古代历法是中国劳动人民智慧的结晶,《尚书·尧典》记载“期三百有六旬有六日,以闰月定四时成
岁”,指出闰年有366天.元代郭守敬创造了中国古代最精密的历法——《授时历》,规定一年为365.2425天,
和现行公历格里高利历是一样的,但比它早了300多年.现行公历闰年是如下确定的:①能被4整除,但不能被
学科网(北京)股份有限公司100整除;②能被400整除,满足以上两个条件之一的年份均为闰年,则公元 年,距上一个闰年的年数为
_____.
14.已知曲线 和圆 有2个交点,则实数 的取值范围是_____________.
四、解答题:本题共5小题,共77分.解答应写出文字说明、证明过程或演算步骤.
15.(13分)
在 中,角 的对边分别为 .已知 ,且 .
(1)若 ,垂足为 ,求BD的长;
(2)若 ,求 的长.
16.(15分)
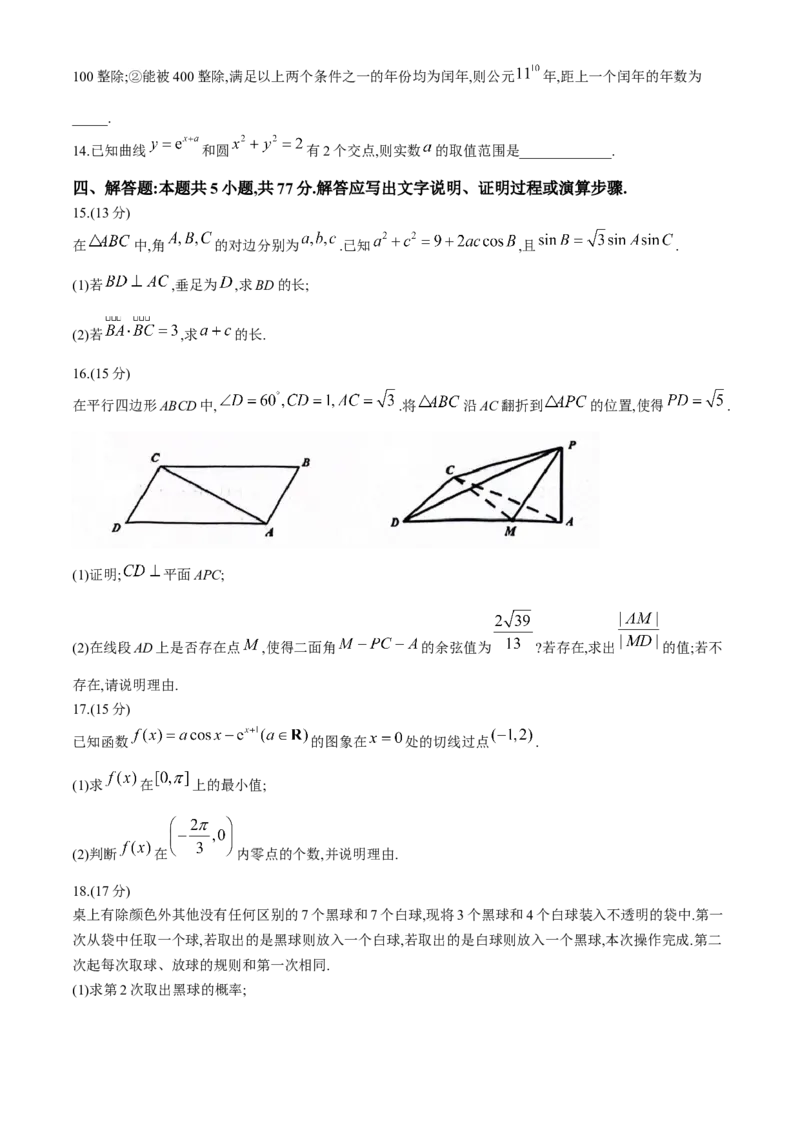
在平行四边形ABCD中, .将 沿AC翻折到 的位置,使得 .
(1)证明; 平面APC;
(2)在线段AD上是否存在点 ,使得二面角 的余弦值为 ?若存在,求出 的值;若不
存在,请说明理由.
17.(15分)
已知函数 的图象在 处的切线过点 .
(1)求 在 上的最小值;
(2)判断 在 内零点的个数,并说明理由.
18.(17分)
桌上有除颜色外其他没有任何区别的7个黑球和7个白球,现将3个黑球和4个白球装入不透明的袋中.第一
次从袋中任取一个球,若取出的是黑球则放入一个白球,若取出的是白球则放入一个黑球,本次操作完成.第二
次起每次取球、放球的规则和第一次相同.
(1)求第2次取出黑球的概率;
学科网(北京)股份有限公司(2)记操作完成 次后袋中黑球的个数为变量 .
(i)求 的概率分布列及数学期望 ;
(ii)求 的数学期望 .
19.(17分)
坐标平面 上的点 也可表示为 ,其中 为 轴非负半轴绕原点 逆时
针旋转到与OP重合的旋转角.将点 绕原点 逆时针旋转 后得到点 ,这个过程称之为旋转变换.
(1)证明旋转变换公式: 并利用该公式,求点 绕原点 逆时针旋转 后的点
的坐标;
(2)旋转变换建立了平面上的每个点 到 的对应关系.利用旋转变换,可将曲线通过旋转转化为我们熟悉的
曲线进行研究.
(i)求将曲线 绕原点 顺时针旋转 后得到的曲线方程,并求该曲线的离心率;
(ii)已知曲线 ,点 ,直线AB交曲线 于 , 两点,作 的外角平分
线交直线AB于点 ,求|FM|的最小值.
学科网(北京)股份有限公司2024 届宁德市普通高中毕业班五月份质量检查
数学试题参考答案及评分标准
说明:
1.本解答指出了每题要考察的主要知识和能力,给出一种或几种解法供参考.如果考生的解法与给出的解
法不同,可根据试题的主要考察内容比照评分标准确定相应的评分细则.
2.对解答题,当考生的解答在某一步出现错误,但整体解决方案可行且后续步骤没有出现推理或计算错误,
则错误部分依细则扣分,并根据对后续步骤影响的程度决定后继部分的给分,但不得超过后续部分正确解
答应给分数的一半;如果后继部分的解答有较严重的错误,就不再给分.
3.解答右端所注分数,表示考生正确做到这一步应得的累加分数.
4.解答题只给整数分数,填空题不给中间分.
一、选择题:本题考查基础知识和基本运算,每小题5分,满分40分.
1.B 2.D 3.D 4.B 5.B 6.C 7.C 8.A
二、选择题:本题共3小题,每小题6分,共18分.在每小题给出的选项中,有多项符合题
目要求.全部选对的得6分,部分选对的得部分分,有选错的得0分.
9.AC 10.BD 11.ABC
11.解法一:对于选项 ,令 ,得 ,所以 或 .
令 ,得 ,由 的值域为 ,
所以当 时,得 ,不合题意,所以 . 正确.
对于选项 ,令 ,得 ,所以 或 .
令 ,得 ,得 ,
因为 的值域为 ,所以 .
令 ,得 ,所以 或 .
因为值域为 ,所以 正确.
对于选项 ,令 ,得 ,因为 ,
则 ,所以函数 为偶函数,图像关于 对称, 正确.
对于选项 ,由值域 和偶函数, 错误.选 .
解法二:由 ,则 ,
学科网(北京)股份有限公司得 ,
设 ,得 ,可设 ( 为正偶数), ,
不妨设 ,可判断 正确, 错误.选 .
三、填空题:本题考查基础知识和基本运算,每小题5分,满分20分.
12. 13.5 14.
四、解答题:本大题共6小题,满分70分,解答须写出文字说明、证明过程和演算步骤.
15.本题主要考查正弦定理、余弦定理、三角形面积公式等基础知识,考查逻辑推理能力、运算求解能力,
考查数形结合思想、化归与转化思想、函数与方程思想等,考查直观想象、逻辑推理、数学运算等核心素
养,体现基础性与综合性.满分13分.
解:(1)由 及余弦定理,得
…………………………………………………………...2分
由 及正弦定理,
得 ,.…………………………………………………………...4分
因为 的面积
所以 .…………………………………………………….6分
(2)由 得 ①,.……………………………………………………7分
因为 ,
所以 ,②……………………………………………………………8分
由①②得 ,………………………………………………………9分
又 ,故 ,.………………………………………………………………10分
学科网(北京)股份有限公司从而 .……………………………………………………….11分
得 ,………………………………………………………………12分
所以 .……………………………………………………………….13分
16.本小题主要考查空间解三角形、直线与直线、直线与平面、平面与平面的位置关系,空间角的计算等基
础知识,考查空间想象能力、逻辑推理能力、运算求解能力,考查数形结合思想、化归与转化思想等,考查直
观想象、逻辑推理、数学运算等核心素养,体现基础性与综合性.满分15分.
解:(1)证明:翻折前,因为四边形ABCD为平行四边形, ,
在三角形ACD中,由正弦定理可得 ………………….1分
,又 ,故 ..……………………………………………………2分
所以 ,即 ,.…………………………………………………………………………3分
因为 ,所以 ,则有 ...………………………………5分
平面APC,所以 平面APC,.…………………………………………6分
(2)由(1)CD⊥平面APC,且 平面ADC,
所以平面 平面APC.
在平行四边形ABCD中, ,即 ,
故 平面ADC...………………………………………………………………………………7分
以点 为坐标原点, 的方向分别为 轴的正方向建立空间直角坐标系,则
,…………………………………………………8分
学科网(北京)股份有限公司设 ,其中 ,
则 ,.……………9分
设平面MCP的法向量为 ,
则 ,取 ,则 ,
所以, ,………………………………………………………11分
易知平面CPA的一个法向量为 ,………………………………………………12分
则 ,整理可得 ,
因为 ,解得 ,………………………………………………………………………14分
因此,线段PC上存在点 ,使二面角 的余弦值为 ,且 .…………15分
17.本小题主要考查导数及其应用、函数的零点和不等式等基础知识,考查逻辑推理能力、运算求解能力等,
考查函数与方程思想、化归与转化思想、分类与整合思想、数形结合思想,考查数学抽象、逻辑推理、直观
想象、数学运算等核心素养,体现基础性与综合性.满分15分.
解法一:(1) ,..…………………………………………2分
又 ,所以切线方程为 ,..……………………………………3分
又切线过点 ,
得 ,所以 ..…………………………………………………………………………4分
所以 ,
当 时, ,所以 在 上单调递减,……………………………………6分
所以 的最小值为 .………………………………………………………7分
(2)判断 在 零点个数,等价于判断方程 根的个数,
学科网(北京)股份有限公司等价于判断方程 根的个数. ………………………………………………………8分
令
,令 ,则 ,得 ..……………………10分
当 时, 在 单调递增;
当 时, 在 单调递减.……………………12分
,
(或 )
所以 时,方程 有2根,
所以 在 有2个零点. .……………………………….15分
解法二:(1) ,……………………………….2分
所以切线方程为 ,………………………………………………………….3分
因此切点为 ,
得 ,所以 ,.………………………………………………………….4分
所以 ,
当 时, ,所以 在 上单调递减,…………………………6分
所以 的最小值为 …………………………………………………….7分
学科网(北京)股份有限公司(2)由(1)得 ,………………………………….8分
令 ,则 在 上为减函数,…………………………….9分
,
所以在 上 必有一个零点 ,使得 ,…………………………10分
从而当 时, ,当 时, ,
所以 在 上单调递增,在 上单调递减..…………………………11分
又 ,…………………………12分
所以在 上 必有一个零点 ,使得 .……………………………………………12分
当 时, ,即 ,此时 单调递增;
当 时, ,即 ,此时 单调递减..………………………………13分
又因为 ,
所以 在 上有一个零点,在 上有一个零点.……………………….14分
综上, 在 有且只有2个零点.………………………………….15分
18.本小题主要考查全概率公式、概率的分布列及期望、递推数列及等比数列等基础知识,考查数学建模能
力、运算求解能力、数据处理能力、应用意识,考查或然与必然思想、化归与转化思想,考查数学抽象、逻
辑推理、数学建模、数据分析和数学运算等核心素养,体现基础性、综合性与创新性.满分17分.
(1)记第 次取出的球是黑球为事件 ,
学科网(北京)股份有限公司则 ,………………………………………………………………1分
根据全概率公式得
所以第2次取出黑球的概率为 .
(2)(i)由题知得 的可能取值为:1,3,5………………………………………………….5分
则 ;………………8分
故 的分布列为:
1 3 5
所以 .…………………………….9分
(ii)设第 次完成操作后袋中黑球数为
则
……………………………………13分
(也可以按如下方法得出递推关系:
学科网(北京)股份有限公司(若通过特殊性入手得出递推关系得2分)
即 ,由此得 ,………………………………15分
又因为 ,…………………………………………………………………16分
所以 ,即 .…………………………………17分
19.本题主要考查两角和与差的正、余弦公式、双曲线、椭圆、直线与椭圆的位置关系等基础知识,考查逻
辑推理能力、运算求解能力和创新能力,考查化归与转化思想、数形结合思想,考查数学抽象、逻辑推理、
直观想象、数学运算等核心素养,体现基础性、综合性与创新性,满分17分.
(1)证明:设 ,由题意可知
所以 ..……………………………………………………2分
故当 ,且 时,
所以 ..………………………………………….4分
(2)(i)设曲线 上的任一点 绕原点 顺时针旋转 后得到的点为 ,可视为 绕原点
逆时针旋转 后得到的点 ,
学科网(北京)股份有限公司所以 ..…………………………………………6分
由点 在曲线 上,所以
整理得 ,.………………………………………………8分
即曲线 绕原点 顺时针旋转 后得到的曲线方程为 ,
该曲线为双曲线,离心率为2. …………………………………………………………………….9分
(ii)由曲线 ,可知当点 满足曲线方程时,点 也满足该曲线方程,
故曲线 关于直线 和 对称,10分设曲线 上任一点 绕原点 顺时针旋转 后得到的
点为 ,
则 ..………………………………………………11分
由点 在曲线 上,所以 ,
即旋转 后得到的曲线方程为椭圆: ,其右焦点坐标为 ,………………………12分
(1)可知,其为点 绕原点 顺时针旋转 后得到的点,
故点 为原椭圆 的右焦点.
由FM为 的外角平分线,
学科网(北京)股份有限公司所以 ,故 ………………13分
设 ,
同理 ,…………………………………………………14分
设 ,显然 在线段AB的延长线或反向延长线上,
所以 ,.………………………………………………………15分
所以 ,
,得 ………………………………………………16分
所以点 的轨迹为直线 ,故 到 的最短距离为 ………………17分
学科网(北京)股份有限公司