文档内容
【赢在高考·黄金8卷】备战2024年高考数学模拟卷(全国卷专用)
黄金卷02
(考试时间:120分钟 试卷满分:150分)
第 I 卷(选择题)
一、选择题:本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题
目要求的.
1.设集合 ,则 ( )
A. B. C. D.
【答案】B
【分析】先化简集合,再利用集合的交并补运算求解即可,
【详解】由题意得 , ,
则 ,则 ,故A错误;
,或 ,则 ,故B正确;
又 , ,故C错误;
,故D错误.
故选:B.
2.设复数 满足 ,则 ( )
A. B. C. D.
【答案】C
【分析】设 ,根据复数相等即可求出 , ,进而求解.
【详解】设 ,则 ,整理得 ,
所以 ,所以 ,所以 ,所以 .
故选:C
3.命题 :函数 的最大值为 ,函数 的最小值为 ;命题 : 的最大
值为 ,则 是 的( )
A.充分不必要条件 B.必要不充分条件
C.充要条件 D.既不充分又不必要条件
【答案】D
【分析】取特殊函数方法判断充分必要条件即可.
【详解】设 , 分别存在最大值 和最小值 ,则
的最大值为 ,所以充分性不成立;
设 , , 取得最大值为1,但 不存在最小
值,所以必要性不成立.
故选:D.
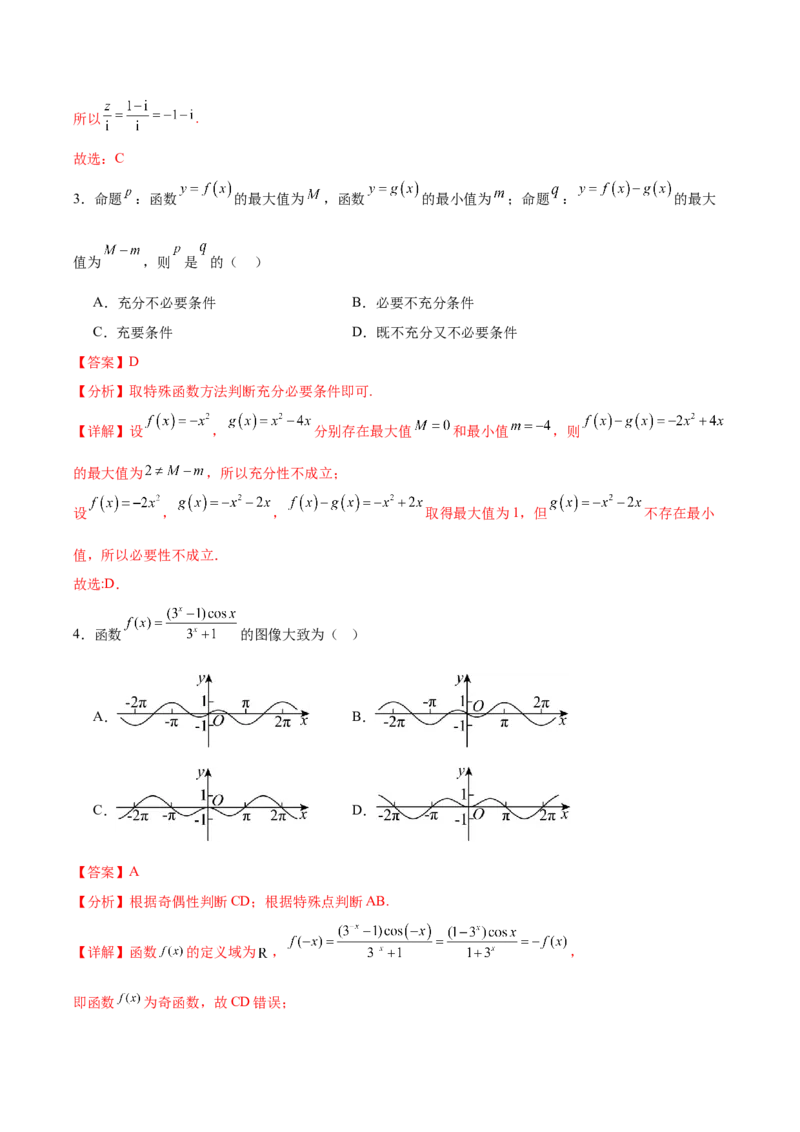
4.函数 的图像大致为( )
A. B.
C. D.
【答案】A
【分析】根据奇偶性判断CD;根据特殊点判断AB.
【详解】函数 的定义域为 , ,
即函数 为奇函数,故CD错误;由 可知,C错误,A正确;
故选:A
5.已知向量 ,且 ,则实数 构成的集合是( )
A. B.
C. D.
【答案】C
【分析】利用向量坐标运算,及向量垂直的坐标表示求解即得.
【详解】向量 ,则 ,
由 ,得 ,即 ,解得 ,
所以实数 构成的集合是 .
故选:C
6.若两个正实数 满足 ,且不等式 有解,则实数 的取值范围是( )
A. B. C. D.
【答案】D
【分析】妙用“1”求 ,然后解一元二次不等式 即可.
【详解】不等式 有解,等价于 ,
因为 ,所以 ,
所以 ,当且仅当 ,即 时等号成立.
所以 ,即 ,解得 或 .
故选:D
7.为落实立德树人的根本任务,践行五育并举,某学校开设 三门劳动教育校本课程,现有甲、乙、
丙、丁、戊五位同学报名参加该校劳动教育校本课程的学习,每位同学仅报一门,每门至少有一位同学参
加,则不同的报名方法有( )
A.60种 B.150种 C.180种 D.300种
【答案】B
【分析】对五位同学分3组,有两种情况,然后分类讨论各自情况种数,采用加法原理求解即可.
【详解】根据题意,甲、乙、丙、丁、戊五位同学选 三门德育校本课程,
每位同学仅报一门,每门至少有一位同学参加,需要分三组,有两类情况,
①三组人数为1、1、3,此时有 种;
②三组人数为2、2、1,此时有 种.
所以不同的报名方法共有60+90=150种.
故选:B.
8.已知 其中 则 ( )
A. B. C. D.
【答案】C
【分析】先根据两角和与差得正弦余弦公式构造并计算出 , ,再根据同角三角函数商数关系计
算出 ,同理计算出 ,最后代入即可算出.
【详解】因为 , ,得 ,所以 ,所以 , ,所以 ,
因为 , ,得 ,所以 ,
, ,所以
,
所以 .
故选: .
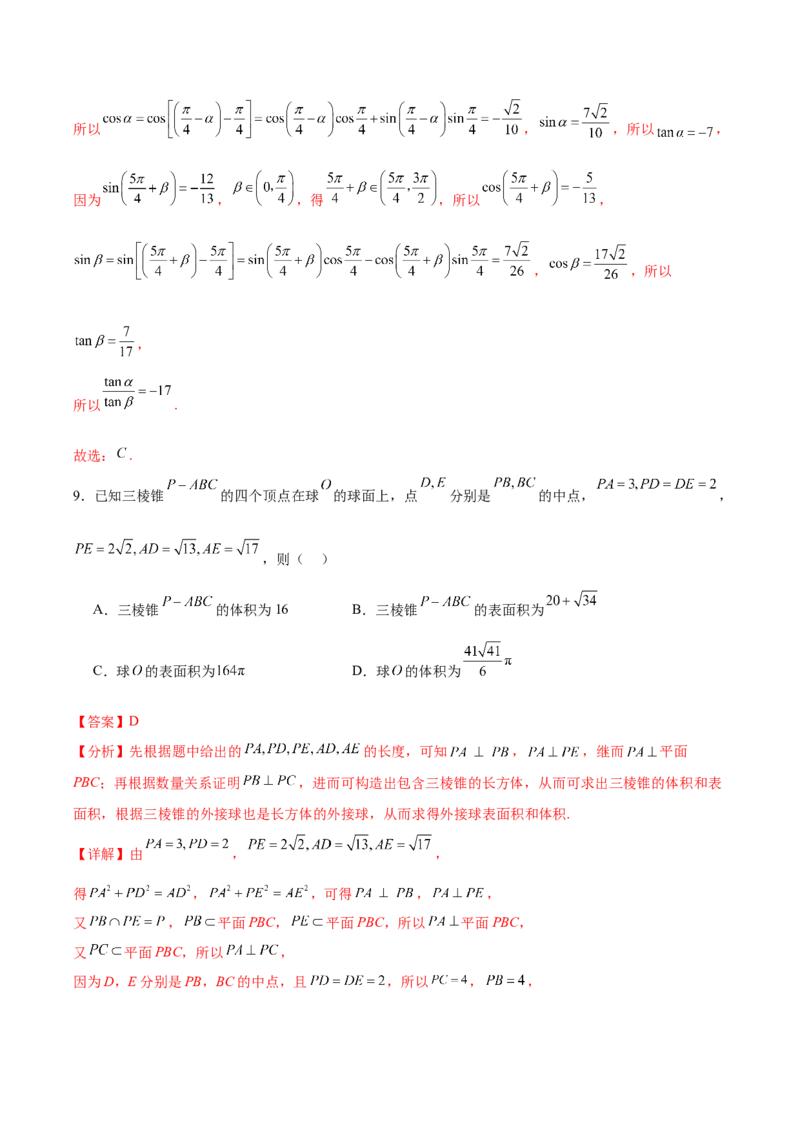
9.已知三棱锥 的四个顶点在球 的球面上,点 分别是 的中点, ,
,则( )
A.三棱锥 的体积为16 B.三棱锥 的表面积为
C.球 的表面积为 D.球 的体积为
【答案】D
【分析】先根据题中给出的 的长度,可知 , ,继而 平面
PBC;再根据数量关系证明 ,进而可构造出包含三棱锥的长方体,从而可求出三棱锥的体积和表
面积,根据三棱锥的外接球也是长方体的外接球,从而求得外接球表面积和体积.
【详解】由 , ,
得 , ,可得 , ,
又 , 平面PBC, 平面PBC,所以 平面PBC,
又 平面PBC,所以 ,
因为D,E分别是PB,BC的中点,且 ,所以 , ,又 ,所以 ,有 ,得 ,
故 两两互相垂直,故可将三棱锥 放在长方体中,如图:
则三棱锥外接球的直径等于该长方体的对角线,设其外接球 的半径为R,
则 ,所以 ,所以球 的表面积为 ,
球 的体积为 ,故选项C错误,D正确.
三棱锥 的体积为 ,
在 中, ,点 分别是 的中点,
则 的高 ,所以 ,
三棱锥 的表面积为 ,
故选项AB错误.
故选:D.
10.已知双曲线 : ( , )的右焦点为 , 、 两点在双曲线的左、右两支上,
且 , , ,且点 在双曲线上,则双曲线的离心率为( )
A. B. C. D.
【答案】B【分析】设双曲线的左焦点为 ,连接 ,则由题意可得四边形 为矩形,设 ,
则 , ,分别在 和 中,运用勾股定理,结合离心率公
式可求得结果.
【详解】设双曲线的左焦点为 ,连接 ,
因为 ,所以 ,
因为 ,所以 ,
因为 ,所以四边形 为矩形,
设 ( ),则 , ,
在 中, ,
所以 ,化简得 ,解得 ,
在 中, ,
所以 ,所以 ,
所以 ,得 ,
所以离心率 ,
故选:B11.已知定义在 上的函数 满足 , 为 的导函数,当
时, ,则不等式 的解集为( )
A. B.
C. D.
【答案】C
【分析】由题意设 ,结合题意可得 ,即函数 是定义在 上的奇函数,又
当 , 时, ,则 ,可得 在 , 上单调递增,在 , 上单
调递增,利用单调性,即可得出答案.
【详解】令 ,
则 ,即 ,
故函数 是定义在 上的奇函数,
当 , 时, ,则 ,
故 在 , 上单调递增,在 , 上单调递增,所以 在 上单调递增,
又 ,则 ,
则不等式 ,即 ,
故 ,解得 .
故选:C.
12.已知数列 的前 项和为 ,且 ,则下列四个结论中正确的个数是( )
① ;
②若 ,则 ;
③若 ,则 ;
④若数列 是单调递增数列,则 的取值范围是 .
A.1 B.2 C.3 D.4
【答案】C
【分析】由 ,可得 ,两式相减得到 ,进而可得
,可判断①,根据 的值可判断 是否为等差,再根据等差数列得前 项和公式即可
求解②③;根据条件得 , ,再根据数列 单调递增,则必有
,且 ,求解即可得出 的取值范围.
【详解】因为 ,当 , ,
两式相减得 ,所以 ,两式相减得 ,故①错误,
当 时,令 ,则 , ,得 ,所以 ,
令 ,则 , ,得 ,所以 ,则
,所以 ,
故 奇数项是以 为首项,2为公差的等差数列,偶数项是以 为首项,2为公差的等差数列,
则
,所以②正确;
当 时,令 ,则 , ,得 ,所以 ,
令 ,则 , ,得 ,
故 偶数项是以 为首项,2为公差的等差数列,奇数项从第二项开始以 为首项,2为公差的
等差数列,
则
,所以③正确;
由于 , , ,
则 ,
又数列 单调递增,则
必有 ,且 ,
所以 ,且 ,解得 ,
所以 的取值范围是 ,所以④正确.
故选:C.第 II 卷(非选择题)
二、填空题:本大题共4小题,每小题5分,共20分
13.(广西壮族自治区玉林市2024届高三高中毕业班第一次摸底测试数学试题)已知公差不为零的等差数
列 的前 项和为 ,则
【答案】7
【分析】若公差为 且 ,易得 ,应用等差数列前n项和公式求结果.
【详解】若公差为 且 ,则 ,
由 .
故答案为:7
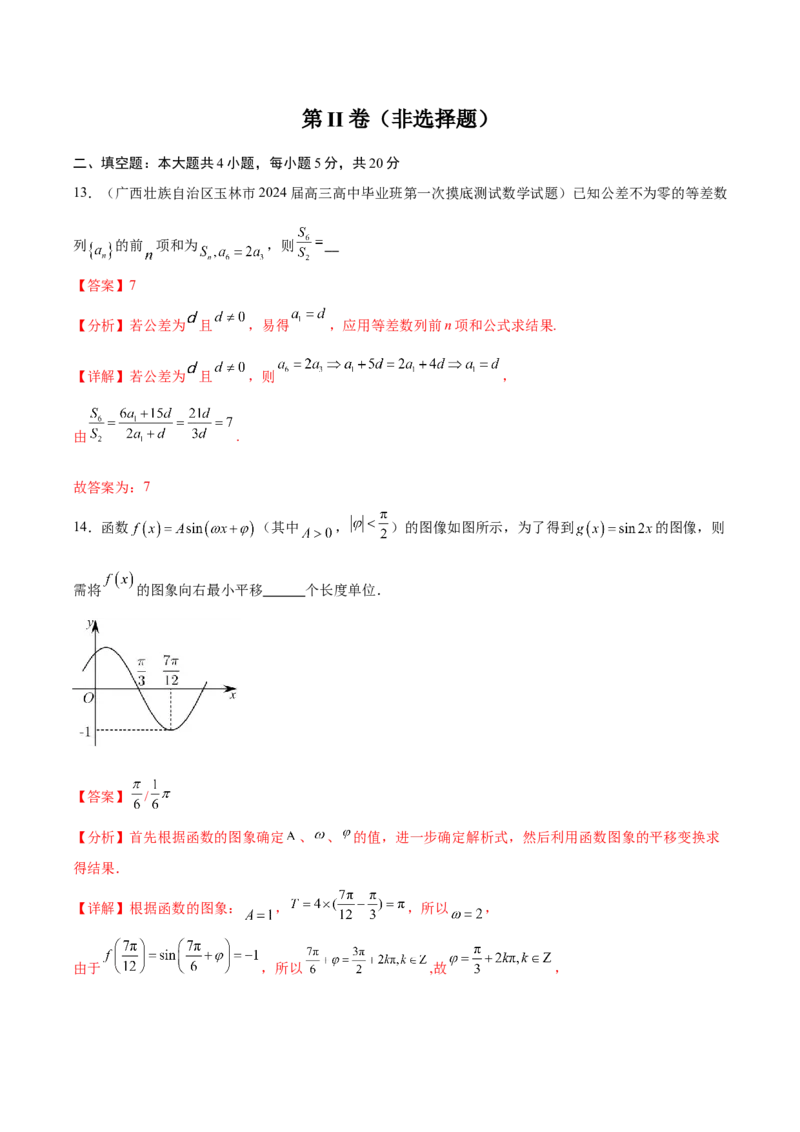
14.函数 (其中 , )的图像如图所示,为了得到 的图像,则
需将 的图象向右最小平移 个长度单位.
【答案】 /
【分析】首先根据函数的图象确定 、 、 的值,进一步确定解析式,然后利用函数图象的平移变换求
得结果.
【详解】根据函数的图象: , ,所以 ,
由于 ,所以 ,故 ,由于 ,取 ,得:
因此
要得到 的图象,则需将 的图象向右最小平移 个单位即可.
故答案为:
15.米斗是称量粮食的量器,是古代官仓、粮栈、米行的必备的用具.为使坚固耐用,米斗多用上好的木
料制成.米斗有着吉祥的寓意,是丰饶富足的象征,带有浓郁的民间文化韵味,如今也成为了一种颇具意
趣的藏品.如图的米斗可以看作一个正四棱台,已知该米斗的侧棱长为10,两个底边长分别为8和6,则
该米斗的外接球的表面积是 .
【答案】
【分析】首先根据正四棱台的对称性得到外接球的球心 所在位置,根据垂直关系列出方程组,解方程组
得外接球半径,最后求出外接球表面积即可.
【详解】由题意,方斗的示意图如下:设棱台上底面中心为 ,下底面中心为 ,
由棱台的性质可知,外接球的球心 落在线段 上,
由题意该四棱台上下底面边长分别为8和6,侧棱长为10,
则 , , ,
所以 ,
设外接球的半径为 , ,则 ,
因为 垂直于上下底面,
所以 ,即 ,又 ,即 ,
联立解得 , ,
所以该米斗的外接球的表面积为 .
故答案为:
16.已知关于 的方程 在 上有两个不相等的实根,则实数 的取值范围是
【答案】
【分析】先利用指、对数性质整理方程为 ,令 , ,即得
在 有两个不相等的实根,再转化为 和 , 有
两个不同的交点,利用导数研究函数图象,并结合图象得到结果即可.
【详解】解: 由 ,则方程 ,即 ,
令 , ,则由 单调性可知,函数 是递增的,故 时,
值域为 .
而 转化为 ,
当 时,方程为 ,不成立,故 ,即转化为 在 有两个不相等的实
根,即 和 , 有两个不同的交点.,当 和 时, ,即 在 上递减,在
上递减;当 时, , 递增.
另外, 时, ; 时, ; .
结合函数 , 图象可知,
当 时, 和 , 的图象有两个不同的交点.
故答案为: .
三、解答题:本大题共70分.解答应写出文字说明、证明过程或演算步骤.第17~21题为必考题,每个试
题考生都必须作答.第22、23题为选考题,考生根据要求作答.
(一)必考题:共60分.
17.(12分)目前,教师职业越来越受青睐,考取教师资格证成为不少人的就业规划之一.当前,中小学教师资
格考试分笔试和面试两部分,笔试通过后才能进入面试环节.已知某市 年共有 名考生参加了中小
学教师资格考试的笔试,笔试成绩 ,只有笔试成绩高于 分的学生才能进入面试环节.
(1)从报考中小学教师资格考试的考生中随机抽取 人,求这 人中至少有一人进入面试的概率;
(2)现有甲、乙、丙 名学生进入了面试,且他们通过面试的概率分别为 ,设这 名学生中通过面试的
人数为 ,求随机变量 的分布列和数学期望.参考数据:若 ,则 , ,
, , .
【答案】(1)
(2)随机变量 的分布列见解析;期望为
【详解】(1)记“至少有一人进入面试”为事件 ,由已知得: ,...........................1分
所以 ,..............................................................3分
则 ,.......................................................................................4分
即这 人中至少有一人进入面试的概率为 .............................................................................5分
(2) 的可能取值为 ,.............................................................................................................6分
,
,
,
,......................................................................................................................9分
则随机变量 的分布列为:
.................................................................................................................................................................11分
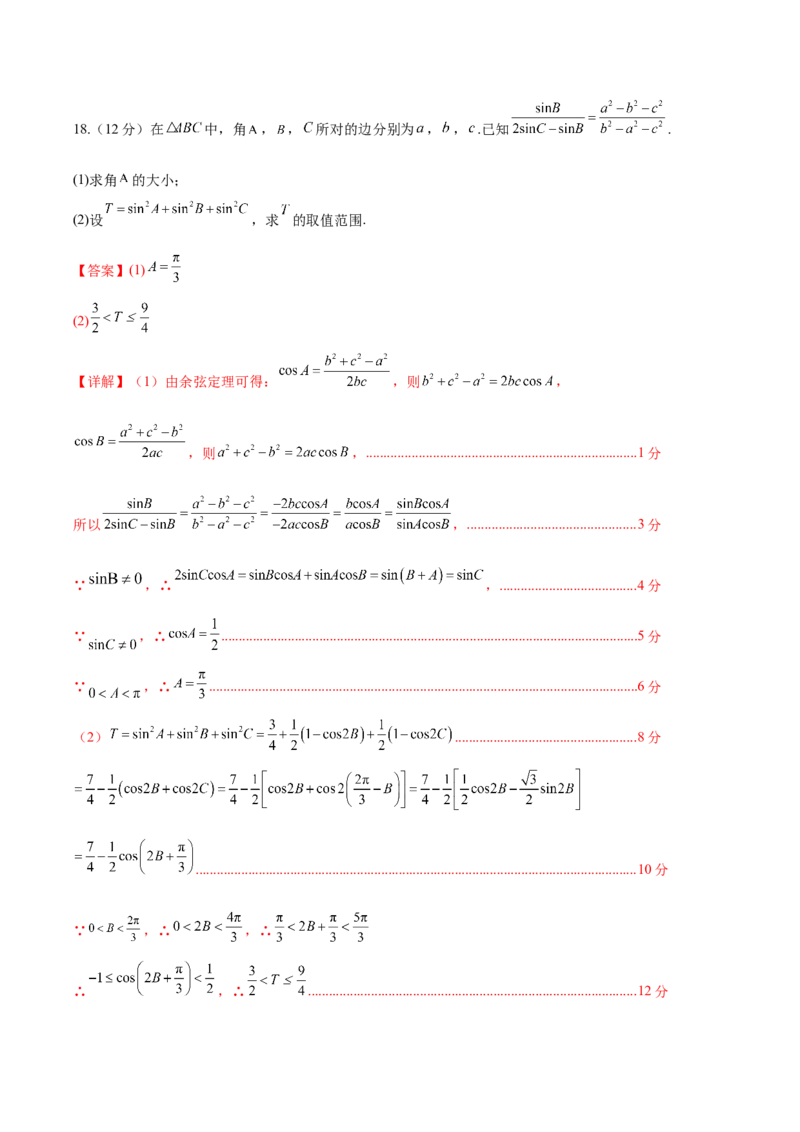
, ...........................................................................................12分18.(12分)在 中,角 , , 所对的边分别为 , , .已知 .
(1)求角 的大小;
(2)设 ,求 的取值范围.
【答案】(1)
(2)
【详解】(1)由余弦定理可得: ,则 ,
,则 ,.............................................................................1分
所以 ,................................................3分
∵ ,∴ ,.......................................4分
∵ ,∴ .......................................................................................................................5分
∵ ,∴ ..........................................................................................................................6分
(2) ....................................................8分
..............................................................................................................................10分
∵ ,∴ ,∴
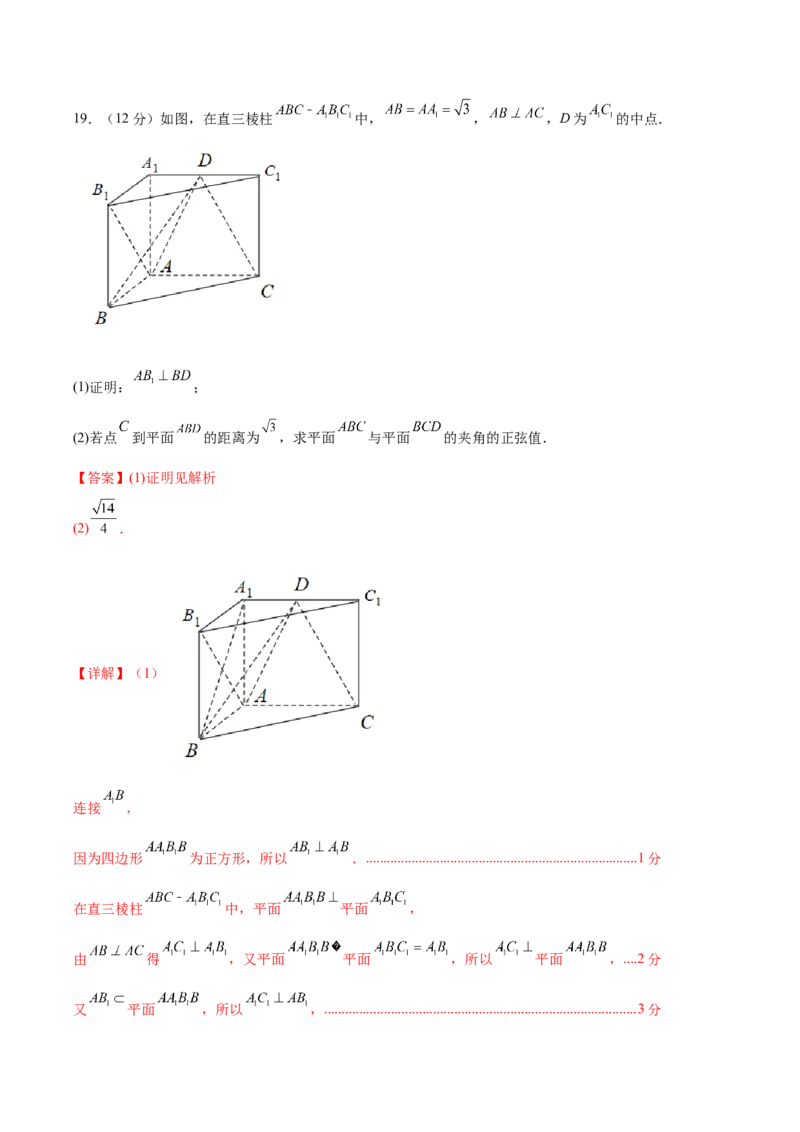
∴ ,∴ ..............................................................................................12分19.(12分)如图,在直三棱柱 中, , ,D为 的中点.
(1)证明: ;
(2)若点 到平面 的距离为 ,求平面 与平面 的夹角的正弦值.
【答案】(1)证明见解析
(2) .
【详解】(1)
连接 ,
因为四边形 为正方形,所以 ..............................................................................1分
在直三棱柱 中,平面 平面 ,
由 得 ,又平面 平面 ,所以 平面 ,....2分
又 平面 ,所以 ,.........................................................................................3分又 , 平面 , 平面 ,所以 平面 ,................4分
又 平面 ,
所以 .......................................................................................................................................5分
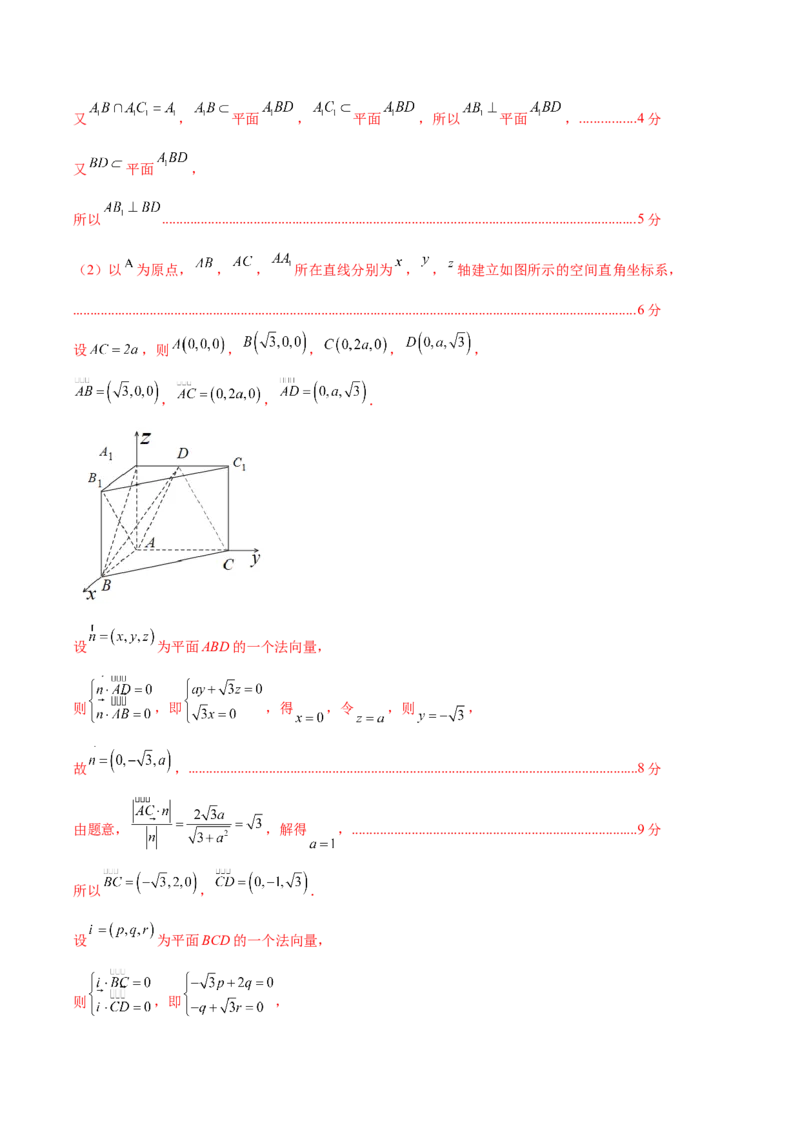
(2)以 为原点, , , 所在直线分别为 , , 轴建立如图所示的空间直角坐标系,
.................................................................................................................................................................6分
设 ,则 , , , ,
, , .
设 为平面ABD的一个法向量,
则 ,即 ,得 ,令 ,则 ,
故 ,................................................................................................................................8分
由题意, ,解得 ,.................................................................................9分
所以 , .
设 为平面BCD的一个法向量,
则 ,即 ,令 ,则 , ,即 ,.................................................................................10分
平面ABC的一个法向量为 ,
设平面 和平面 的夹角为 ,
则 ,....................................................................................11分
所以 ,
所以平面 和平面 的夹角的正弦值为 ......................................................................12分
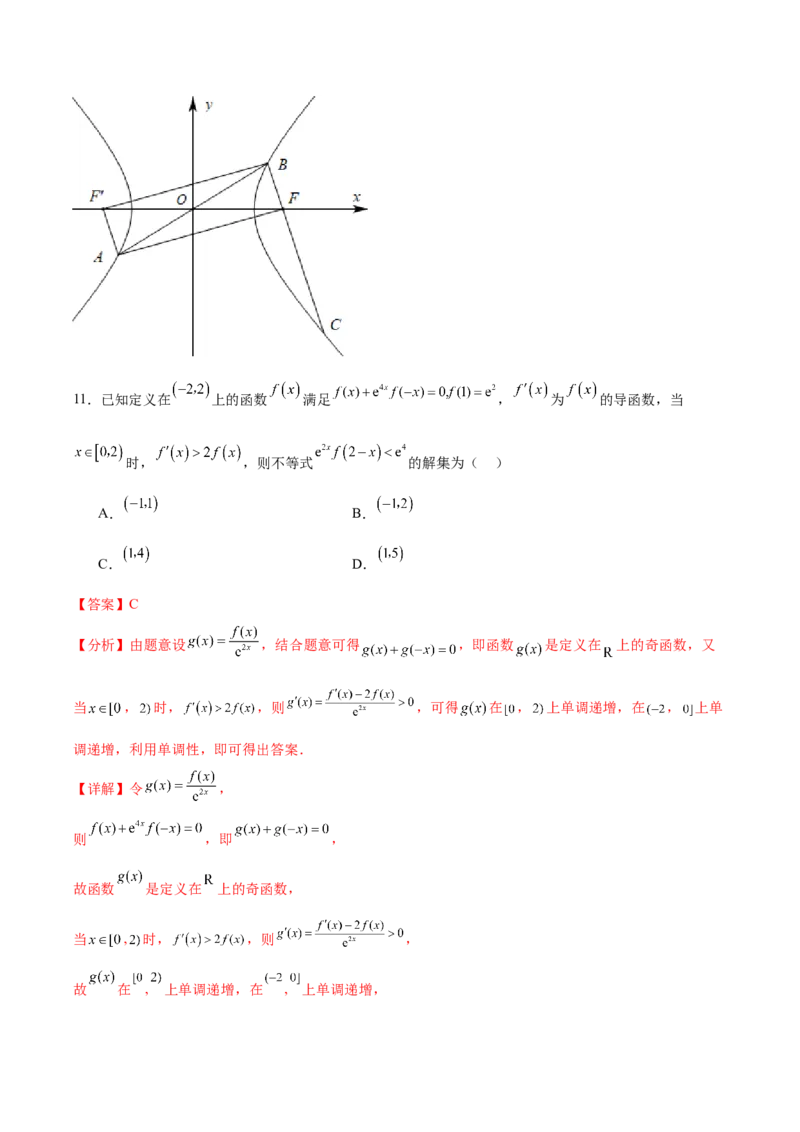
20.(12分)(贵州省遵义市2024届高三第一次质量监测统考数学试题)已知 为椭圆
的两个焦点, 为椭圆 上异于左、右顶点的任意一点, 的周长为6,面积的最大值为 :
(1)求椭圆 的方程;
(2)直线 与椭圆 的另一交点为 ,与 轴的交点为 .若 , .试问: 是否
为定值?并说明理由.
【答案】(1)
(2) ,理由见解析
【详解】(1)设椭圆 的方程为 ,则
由椭圆的定义及 的周长为6,知 ①,....................................................................1分
由于 为椭圆 上异于左、右顶点的任意一点,得 到 轴距离最大为 ,
因为 的面积的最大值为 ,
所以 ②,..............................................................................................................2分又 ③,.................................................................................................................................3分
联立①②③,得 ,
所以椭圆 的方程为 .........................................................................................................4分
(2) 为定值 ,理由如下:.................................................................................................5分
根据已知条件作出图形如图所示,
设 ,则 ,
因为 在椭圆内部,则直线 与椭圆一定有两交点,
联立 消去 得: ,.................................................................7分
,......................................................................................................8分
又 ,且 ,
所以 ,同理 ....................................................................................................10分
所以 .所以 为定值 ...........................................................................................................................12分
21.(12分)已知函数 , .
(1)若 ,求函数 值域;
(2)是否存在正整数a使得 恒成立?若存在,求出正整数a的取值集合;若不存在,请说明理
由.
【答案】(1) ;
(2) .
【详解】(1)由题设 ,则
,.........................................1分
若 ,则 , ,可得 , 递增;
若 ,则 , ,可得 , 递减;.........................................3分
又 ,
综上, ,值域为 .....................................................................................4分
(2)由 , ,则 ,.............................................5分
令 , ,则 ,且 ,当 , ,(舍);..........................................6分
当 ,则 ,故 ,
令 ,则
,
又 ,对于 ,有 ,即 递增,
所以 ,故 恒成立,......................................................................8分
所以 ,即 在 上递增,又 ,则 ,
所以 在 上递增,又 ,即 , ,符合题意;
当 ,令 ,则 , ,........................10分
所以 (舍);.11分
综上,正整数a的取值集合 ..........................................................................................................12分
【点睛】关键点点睛:第二问,问题化为 在 上恒成立,再分类讨
论参数并结合导数研究函数值的符号,再 时令 ,构造出 为关键.
(二)选考题:共10分.请考生在22、23题中任选一题作答,如果多做,则按所做的第一题计分.
选修4-4:坐标系与参数方程
22.(10分)平面直角坐标系 中,曲线 的参数方程为 ( 为参数).以原点O为极点,x
轴的正半轴为极轴建立极坐标系,曲线 的极坐标方程为 .(1)求曲线 的普通方程和曲线 的直角坐标方程;
(2)已知点 ,记 和 交于 两点,求 的值.
【答案】(1)曲线 的普通方程为 ;曲线 的直角坐标方程为
(2)
【详解】(1)已知曲线 ( 为参数),
则 ,由 消参得 ,
则曲线 的普通方程为 ..................................................................................................2分
由曲线 的极坐标方程为 ,
变形得 ,............................................................................................3分
即 ,且满足 ,
由互化公式 ,得 ,即 .
故曲线 的直角坐标方程为 ........................................................................................5分
(2)由于 在直线l上,可设直线l的参数方程的标准形式为 (t为参数),
代入曲线 ,
化简得 , ,............................................................................................7分
设A,B对应的参数分别为 , ,
则 , ,................................................................................................................8分
由于 ,故 ,
所以 .
故 的值为 .....................................................................................................................10分
选修4-5:不等式选讲
23.(10分)已知函数 .
(1)求不等式 的解集 ;
(2)若 是 的最小值,且正数 满足 ,证明: .
【答案】(1)
(2)证明见解析
【详解】(1) ................................................................1分∴ 或 或 ,..................................................................3分
解得 或 或 ,
∴不等式的解集为 ;...........................................................................................5分
(2)证明:由 ,可得 的最小值为 ,...........................................6分
则 , ,
∴
,当且仅当 时,等号成立,.............................................9分
∴ ..................................................................................................................10分