2024届福建省泉州市普通高中毕业班质量监测（三）数学答案_2024年3月_013月合集_2024届福建省泉州市普通高中毕业班质量监测三_2024届福建省泉州市普通高中毕业班质量监测（三）数学

保密★使用前 泉州市 2024 届高中毕业班质量监测（三） 2024.03 高 三 数 学 本试卷共19题，满分150分，共8页。考试用时120分钟。 一、选择题答案： 1.B 2.C 3.C 4．B 5． C． 6． D． 7．A 8．D 二、选择题答案： 9.AD 10.BCD 11.ACD 三、填空题：本题共3小题，每小题5分，共15分。 16 12．5 13.x2 4y 14．e3 3 四、解答题：本题共5小题，共77分。解答应写出文字说明，证明过程或演算步骤。 15．（13分） 如图，在三棱锥PABC中，PAPC AB AC2，BC 2 2，E为PC的中点，点F   在PA上，且EF 平面PAB ，PM PB (R)． （1）若MF‖平面ABC，求； 1 （2）若 ，求平面PAB 与平面MAC夹角的正弦值． 2 【命题意图】本题考查空间点、直线与平面间的位置关系等知识；考查推理论证、运算求解 等能力；考查数形结合思想、化归与转化思想等；体现应用性、创新性、综合 高三数学试题 第1页（共8页） {#{QQABDY4QgggAAAAAAAhCAwVqCAKQkAEACAoGwFAMsAABCBFABAA=}#}性，导向对直观想象、数学运算等核心素养的关注. 解法一：（1）依题意得,△PAC 为正三角形，取PA 中点N， 连结CN ，则CN PA ， 因为EF 平面PAB ，所以EF PA， EF∥CN，·················································································（2分） 1 又因为E为PC的中点，所以F 为PN 中点，则PF  PA ，·················（3分） 4 因为MF∥平面ABC，MF 平面PAB ， 平面PAB 平面ABC AB，即MF∥AB，······································（5分） 1 1 也即PM  PB， . ·······························································（6分） 4 4 （2）因为EF∥CN，则CN 平面PAB ，且CN  3·························（7分） 又因为EF 平面PAB ，所以EF  AB，···········································（8分） 由AB AC 2, BC 2 2 可知BC2  AB2  AC2， 则△ABC为等腰直角三角形，AB AC， 又因为EF 与AC 相交于平面PAC ，所以AB平面PAC ，················· （10分） △PAB 为等腰直角三角形，M 为斜边PB中点，则△PAM 也为等腰直角三角形， 2 取AM 中点H ，则NH  AM ，且NH  ， 2 连结CH ，AM 平面CNH ， 则AM CH ，CHN为二面角PAM C 的平面角， ·····················（11分） 1 14 在Rt△CHN 中， CH  CN2 NH2  3  2 2 高三数学试题 第2页（共8页） {#{QQABDY4QgggAAAAAAAhCAwVqCAKQkAEACAoGwFAMsAABCBFABAA=}#}CN 3 42 sinCHN    . 则 CH 14 7 ····················································（13分） 2 解法二： （1）同解法一； （2）因为EF 平面PAB ，所以EF  AB，······································（7分） 由AB AC 2, BC 2 2 可知BC2  AB2  AC2， 则△ABC为等腰直角三角形，AB AC， 取AC 中点O，连结PO，则PO AC， 取BC中点Q，连结OQ，则OQ∥AB， 又因为EF 与AC 相交于平面PAC ，所以AB平面PAC ，···················（9分） 也即OQ 平面PAC ， 所以OQ，OC，OP两两相互垂直，以O为原点，OQ，OC，OP所在直线分 别为x轴，y轴，z轴，建立空间直角坐标系. 1 3 1 3 3 A(0,1,0)，B(2,1,0)，C(0,1,0)，P(0,0, 3)，E(0, , )，F(0, , )， 2 2 4 4 1 3 1 3 3 3 M(0, , )，AM (1, , )，AC (0,2,0)，EF (0, , )，······（10分） 2 2 2 2 4 4 设平面MAC 的一个法向量n(x,y,z)，则 nAM 0 ， nAC0 ，即  1 3 x y z0,  2 2 取z2，则x 3，  2y0. 所以n( 3,0,2)为平面MAC 的一个法向量. ···································（11分） 3 EFn cosEF，n   2  7 ， EF  n 3 7 7 4 1 42 记平面PAB 与平面MAC 夹角为，sin 1  .···················· （13分） 7 7 解法三： （1）因为EF 平面PAB ，所以EF  AB， 高三数学试题 第3页（共8页） {#{QQABDY4QgggAAAAAAAhCAwVqCAKQkAEACAoGwFAMsAABCBFABAA=}#}由AB AC 2, BC 2 2 可知BC2  AB2  AC2， 则△ABC为等腰直角三角形，AB AC， △PAC 为正三角形，取AC 中点O，连结PO，则PO AC， 取BC中点Q，连结OQ，则OQ∥AB， 又因为EF 与AC 相交于平面PAC ， 所以AB平面PAC ，也即OQ 平面PAC ， ·································· （3分） 所以OQ，OC，OP两两相互垂直，以O为原点，OQ，OC，OP所在直线分 别为x轴，y轴，z轴，建立空间直角坐标系. 1 3 A(0,1,0)，B(2,1,0)，C(0,1,0)，P(0,0, 3)，E(0, , )，PA (0,1, 3)， 2 2 ··································································································（4分） 因为MF∥平面ABC，MF 平面PAB ， 平面PAB 平面ABC AB，则MF∥AB， ·····································（6分）     因为PM PB ，所以PF PA(0,, 3)， F(0,, 3 3)，  1 3   EF (0, ,  3)，EFPA410， 2 2 1 所以 . ················································································（9分） 4 补充说明：第一小题利用坐标法解答得9分，其中证明AB平面PAC 得3分， 请把这3分的分值写到第二小题的得分栏。 1 3 1 3 3 3 （2）M(0, , )，AM (1, , )，AC (0,2,0)，EF (0, , ),（10分） 2 2 2 2 4 4 设平面MAC 的一个法向量n(x,y,z)，则 nAM 0 ， nAC0 ，即 高三数学试题 第4页（共8页） {#{QQABDY4QgggAAAAAAAhCAwVqCAKQkAEACAoGwFAMsAABCBFABAA=}#} 1 3 x y z0,  2 2 取z2，则x 3，  2y0. 所以n( 3,0,2)为平面MAC 的一个法向量. ···································（11分） 3 EFn cosEF，n   2  7 ， EF  n 3 7 7 4 1 42 记平面PAB 与平面MAC 夹角为，sin 1  .···················· （13分） 7 7 解法四： (1)同解法一； (2)设点C在平面PAB 的射影为N，则CN 平面PAB ， 过点N做NH  AM ，垂足为H ，连结CH ，AM 平面CNH ， 则AM CH ，CHN为PAM C 的平面角， 因为EF 平面PAB ，所以EF  AB，··············································（7分） 由AB AC 2, BC 2 2 可知BC2  AB2  AC2， 则△ABC为等腰直角三角形，AB AC， △PAC 为正三角形，取AC 中点O，连结PO，则PO AC， 又因为EF 与AC 相交于平面PAC ，所以AB平面PAC ，···················（9分） ABPO，ABAC A，PO平面ABC 1 1 因为V V ，则 S CN  S PO，所以CN PO 3，（10分） CPAB PACB 3 △PAB 3 △ABC 在△PBC中，PC2， BCBP2 2 ， 高三数学试题 第5页（共8页） {#{QQABDY4QgggAAAAAAAhCAwVqCAKQkAEACAoGwFAMsAABCBFABAA=}#}(2 2)2(2 2)222 3 cosPBC  ， 22 22 2 4 CM2 BM2 BC2 2BM BCcosPBC 4，CM 2，······················（11分） 在△MCA中， AM  2 ，ACMC2，△MCA∽△PBC 1 1 1 7 14 S  AM CH  ACMCsinACM  22 ，CH  ，（12分） △AMC 2 2 2 4 2 CN 3 42 sinCHN    . CH 14 7 ·······················································（13分） 2 16．（15分） 淄博烧烤、哈尔滨冬日冰雪、山河四省梦幻联动、鄂了赣饭真湘……，2023年全国各地 的文旅部门在网络上掀起了一波花式创意宣传，带火了各地的文旅市场，很好地推动国内旅 游业的发展．已知某旅游景区在手机APP上推出游客竞答的问卷，题型为单项选择题，每题 均有4个选项，其中有且只有一项是正确选项．对于游客甲，在知道答题涉及的内容的条件 下，可选出唯一的正确选项；在不知道答题涉及的内容的条件下，则随机选择一个选项．已 1 知甲知道答题涉及内容的题数占问卷总题数的 ． 3 （1）求甲任选一题并答对的概率； （2）若问卷答题以题组形式呈现，每个题组由2道单项选择题构成，每道选择题答对得2 2 分，答错扣1分，放弃作答得0分．假设对于任意一道题，甲选择作答的概率均为 ，且两 3 题是否选择作答及答题情况互不影响，记每组答题总得分为X ． （i）求P(X 4)和P(X 2)； （ii）求E(X)． 【命题意图】本小题主要考查全概率、独立事件、分布列、数学期望、等基础知识，考查运 算求解、推理论证、数据处理能力，体现综合性、创新性、应用性，导向对发 高三数学试题 第6页（共8页） {#{QQABDY4QgggAAAAAAAhCAwVqCAKQkAEACAoGwFAMsAABCBFABAA=}#}展数学运算、逻辑推理、数据分析、数学建模等核心素养的关注． 【试题简析】（1）记“甲任选一道题并答对”为事件M ，“甲知道答题涉及内容”为事件A． ········································································································1分 1 2 1 依题意，P(A) ，P(A) ，P(M A)1，P(M A) ．·······················2分 3 3 4 因为事件MA与MA互斥，所以P(M)P(MAMA)P(MA)P(MA) （没说明互斥不扣分）3分 ········································································· 1 P(M A)P(A)P(M A)P(A) ．·······················（公式1分，结果1分）5分 2 2 1 2 1 1 （2）（ⅰ）P(X 4)     ．··················································· 7分 3 2 3 2 9 2 1 2 1 1 P(X 2)     ；··（本小题答对任意一个2分，答对两个3分）8分 3 2 3 2 9 （ⅱ）依题意，随机变量X 2,1,0,1,2,4．·······（部分对1分，全对2分）10分 1 2 1 2 P(X 1)2    ；······························································11分 3 3 2 9 1 1 1 P(X 0)   ；········································································ 12分 3 3 9 2 1 2 1 2 P(X 1)2     ；··························································· 13分 3 2 3 2 9 1 2 1 2 P(X 2)2    ；································································14分 3 3 2 9 1 2 1 2 2 1 2 故E(X)(2) (1) 0 1 2 4  ．·······················15分 9 9 9 9 9 9 3 17．（15分） 1 lnx1 （1）已知x[ ,1]，求 f(x) 的最大值与最小值； 2 x2 （2）若关于x的不等式lnxax2 1存在唯一的整数解，求实数a的取值范围． 【命题意图】本小题主要考查导数的应用、不等式等基础知识，考查运算求解、推理论证、 数形结合、转化化归等能力，体现综合性、创新性，导向对发展数学运算、逻 辑推理、直观想象等核心素养的关注． 【试题简析】 高三数学试题 第7页（共8页） {#{QQABDY4QgggAAAAAAAhCAwVqCAKQkAEACAoGwFAMsAABCBFABAA=}#}1 (2lnx1) （1） 因为x[ ,1]， f '(x) ，······················································ 1分 2 x3 e 令 f '(x)0，解得x ，··································································2分 e f '(x)， f(x)的变化情况如下表所示. 1 e e e x ( , ) ( ,1) 2 e e e f '(x)  0  e f(x) 单调递增 单调递减 2 ········································································································4分 1 e e 所以， f(x)在区间( , )上单调递增，在区间( ,1)上单调递减. 2 e e e e 当x 时， f(x)有极大值 ，也是 f(x)的最大值.·································5分 e 2 1 又因为 f( )44ln2， f(1)1， 2 1 而(44ln2)134ln2lne3ln160 ，所以 f( ) f(1)，·····················6分 2 所以 f(1)1为 f(x)的最小值.································································7分 （2） lnx1 解法一：因为x 0，所以不等式lnxax2 1可化为a f(x) .·····················8分 x2 由（1）可知 lnx1 e e f(x) 在区间(0, )上单调递增，在区间( ,)上单调递减. x2 e e e e 因为 f(x)的最大值 f ( )= ， f(1)1， ·············································9分 e 2 1 1ln2 1 e f ( )0  f(1)， f(2)  f(1)，  12 e 4 e e 所以xN*，x1时， f(x)最大，····························（有相应解释即可）10分 所以不等式lnxax2 1即a f (x)存在唯一的整数解只能为1， ······················································（整步只提供图形没有解释扣2分）11分  f(1)a 所以 ，················································································13分 f(2)a 高三数学试题 第8页（共8页） {#{QQABDY4QgggAAAAAAAhCAwVqCAKQkAEACAoGwFAMsAABCBFABAA=}#}1ln2 ln2e 所以a的取值范围为 a1.（或[ ,1)）···································15分 4 4 解法二：令g(x)lnxax2 1(x0)，由题意可知g(x)0有唯一整数解，·················8分 12ax2 g'(x) ， x 12ax2 当a0时，g'(x) 0，所以g(x)在(0,)单调递增， x 而g(1)1a0，所以g(2)g(1)0，与题意矛盾；································9分 12ax2 2a 2a 当a0时，由g'(x) 0可得x 或x （舍去）， x 2a 2a 2a 2a 当x(0, )时，g'(x)0，x( ,)时，g'(x)0， 2a 2a 2a 2a 所以g(x)在(0, ]单调递增，在[ ,)单调递减， 2a 2a 2a 1 所以x 时，g(x)取最大值为ln 2a  ，·····································10分 2a 2 1 e 由题意可知ln 2a  0，解得0a ，········································· 11分 2 2 因为g(1)1a，所以当g(1)1a0即0a1时， 1ln2 由g(x)0有唯一整数解知g(2)ln24a10，解得 a1，·······12分 4 2a 2a 若12 ，由g(x)在(0, ]单调递增知0 g(1) g(2)0 ，矛盾 2a 2a 2a 2a 所以2 ，由g(x)在[ ,)单调递减可知x[2,)，g(x)0 2a 2a 1ln2 所以 a1符合题意；······························································ 13分 4 2a 2 当a1时，  ，g(1)1a0， 2a 2 2a 由g(x)在[ ,)单调递减可知x[1,)，g(x)g(1)0，不符合题意； 2a ······································································································14分 1ln2 ln2e 综上所述，a的取值范围为 a1.（或[ ,1)）··························15分 4 4 18．（17分） (a,b)表示正整数a,b的最大公约数．若{x,x ,,x }{1,2,,m}（k,mN*），且 1 2 k 高三数学试题 第9页（共8页） {#{QQABDY4QgggAAAAAAAhCAwVqCAKQkAEACAoGwFAMsAABCBFABAA=}#}x{x,x ,,x }，(x,m)1，则将k的最大值记为(m)，例如：(1)1,(5)4． 1 2 k （1）求(2),(3),(6)； （2）已知(m,n)1时，(mn)(m)(n)． （i）求(6n)； 1 6 （ii）设b  ，数列{b }的前n项和为T ，证明：T  ． n 3(6n)1 n n n 25 【命题意图】本小题主要考查等比数列的通项公式与数列求和等基础知识，考查运算求解能 力，考查函数与方程、化归与转化等思想，体现基础性，导向对发展数学运算等 核心素养的关注． 【试题解析】（1）依题可得(m)表示所有不超过正整数m，且与m互质的正整数的个数， 因为与2互质的数为1，所以(2)1；····················································1分 因为与3互质的数为1,2，所以(3)2；·················································2分 因为与6互质的数为1,5，所以(6)2；················································3分 （2）①因为[1,2n]中与2n互质的正整数只有奇数， 所以[1,2n]中与2n互质的正整数个数为2n1，所以(2n)2n1，··················· 5分 又因为[3k2,3k]（k 1,2,,3n1）中与3n互质的正整数只有3k2与3k 1两 个，所以  1,3n  中与3n互质的正整数个数为23n1，所以  3n 23n1， ········································································································7分 所以(6n)(2n)(3n)26n1.·····························································9分 1 1 ②解法一：因为b  ，所以b  ．···································10分 n 3(6n)1 n 6n 1 1 所以b  ．··············································································13分 n 56n1 1 令c  1 ,因为 c n1  56n  1 , n 56n1 c 1 6 n 56n1 1 1 所以数列{c }是以 为首项， 为公比的等比数列.···································14分 n 5 6 高三数学试题 第10页（共8页） {#{QQABDY4QgggAAAAAAAhCAwVqCAKQkAEACAoGwFAMsAABCBFABAA=}#}1 1 [1( )n] 所以数列{c }的前n项和S  5 6  6 [1( 1 )n].·····························16分 n n 1 25 6 1 6 6 1 1 6 所以T  [1( )n].又因为( )n 0,所以T  ．·································17分 n 25 6 6 n 25 1 1 解法二：因为b  ，所以b  ．······································10分 n 3(6n)1 n 6n 1 1 6n11 又因为b   , n 6n 1 (6n 1)(6n11) 6 [(6n11)(6n 1)] 所以 6n1 5 6 1 1 ,············13分 b    [  ] n (6n 1)(6n11) (6n 1)(6n11) 5 6n 1 6n11 6 1 1 1 1 1 1 1 1 所以T  [        ], n 5 611 62 1 62 1 63 1 63 1 64 1 6n 1 6n11 ······································································································14分 6 1 1 6 6 1 所以T  [  ],所以T   [ ].································16分 n 5 611 6n11 n 25 5 6n11 1 6 因为 0,所以T  .·······························································17分 6n11 n 25 高三数学试题 第11页（共8页） {#{QQABDY4QgggAAAAAAAhCAwVqCAKQkAEACAoGwFAMsAABCBFABAA=}#}19．（17分） 已知中心在原点、焦点在x轴上的圆锥曲线E的离心率为2，过E的右焦点F 作垂直于x 轴的直线，该直线被E截得的弦长为6． （1）求E的方程； （2）若面积为3的△ABC的三个顶点均在E上，边BC过F ，边AB过原点，求直线BC的 方程； （3）已知M(1,0)，过点T( 1 ,2)的直线l与E在y轴的右侧交于不同的两点P,Q，l上是 2     否存在点S满足TPSQPSTQ，且|SM |2 |SF|213？若存在，求S的坐标，若不存在， 请说明理由. 【命题意图】本小题主要考查双曲线的定义，双曲线的标准方程，直线与双曲线的位置关系 等知识；考查运算求解、逻辑推理等能力；考查数形结合、函数与方程等思想； 体现基础性、综合性与创新性，导向对直观想象、逻辑推理、数学运算等核心 素养的关注． 【试题解析】 （1）圆锥曲线E的离心率为2，故E为双曲线，·············································1分 x2 y2 因为E中心在原点、焦点在x轴上，所以设E的方程为  1(a0,b0)， a2 b2 ·····································································································1分 【说明：指出曲线为双曲线，或正确写出曲线的方程形式，均可得1分，但不累计得分】 b2 2b2 令xc，解得y ，所以有 6......① ·······································2分 a a b2 又由离心率为2，得 1 2......②，··················································3分 a2 a2 1 由①②解得 ，··········································································4分 b2 3 y2 所以双曲线E的标准方程是x2  1．··················································4分 3 解法一：（2）设B(x,y ),C(x ,y ) ，由已知，得F2,0，根据直线AB过原点及对称性， 1 1 2 2 高三数学试题 第12页（共8页） {#{QQABDY4QgggAAAAAAAhCAwVqCAKQkAEACAoGwFAMsAABCBFABAA=}#}1 知S 2S 2 OF  y y c y y 2 y y ，······················5分 ABC BOC 2 1 2 1 2 1 2  y2 x2  1 联立方程，得 3 ，化简整理，得(3t2 1)y2 12ty90，···············6分  xty2  12t y  y    1 2 3t2 1 所以 ，且144t2 36(3t2 1)36t2 360，····················7分  y y  9  1 2 3t2 1 6(t2 1) 所以S 2 y y 2 y  y 24y y 2 3 ， ABC 1 2 1 2 1 2 3t2 1 解得 t  3 ， ........ 8分【到此可得第8分】 所以直线BC的方程是x 3y20或x 3y20．·····························8分 解法二：（2）设B(x,y ),C(x ,y ) ，由已知，得F2,0，根据直线AB过原点及对称性， 1 1 2 2 1 知S 2S 2  BC d  BC d （其中d为原点O到直线BC的距离）， ABC BOC 2 ········································································································5分  y2 x2  1 联立方程， 3 ，化简整理，得(3t2 1)y2 12ty90，··················6分  xty2  12t y  y    1 2 3t2 1 所以 ，且144t2 36(3t2 1)36t2 36，························7分  y y  9  1 2 3t2 1 所以 6(t2 1) BC  1t2 y  y 24y y  1t2 y  y 24y y  1t2  ， 1 2 1 2 1 2 1 2 3t2 1 2 6(t2 1) 2 12(t2 1) 又因为d  ，于是S  BC d  1t2   3， 1t2 ABC 3t2 1 1t2 3t2 1 解得 t  3 ，····················································································8分 所以直线BC的方程是x 3y20或x 3y20． 8分 高三数学试题 第13页（共8页） {#{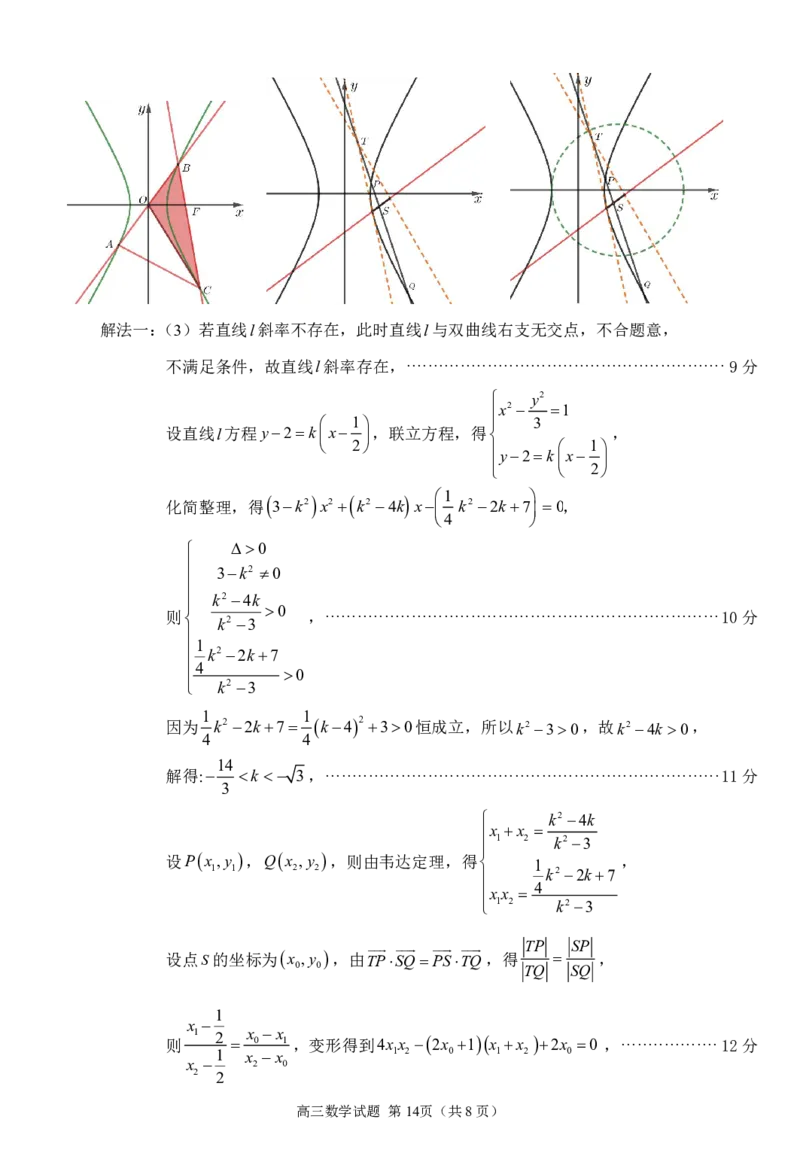QQABDY4QgggAAAAAAAhCAwVqCAKQkAEACAoGwFAMsAABCBFABAA=}#}解法一：（3）若直线l斜率不存在，此时直线l与双曲线右支无交点，不合题意， 不满足条件，故直线l斜率存在，··························································· 9分  y2 x2 1  1  3 设直线l方程y2kx ，联立方程，得 ，  2  y2k  x 1     2 化简整理，得  3k2 x2   k2 4k  x   1 k2 2k7   0， 4   0  3k2 0    k24k 则 k23 0 ，·········································································10分  1 k22k7 4 0   k23 1 1 因为 k22k7 k4230恒成立，所以k230，故k24k 0， 4 4 14 解得: k  3，·········································································11分 3  k24k x x  1 2 k23  设Px,y ，Qx ,y ，则由韦达定理，得 1 ， 1 1 2 2  k22k7 4 xx   1 2 k23     TP SP 设点S的坐标为x ,y ，由TPSQPSTQ，得  ， 0 0 TQ SQ 1 x  则 1 2  x 0 x 1 ，变形得到4xx 2x 1x x 2x 0 ，··················12分 1 x x 1 2 0 1 2 0 x  2 0 2 2 高三数学试题 第14页（共8页） {#{QQABDY4QgggAAAAAAAhCAwVqCAKQkAEACAoGwFAMsAABCBFABAA=}#}1 k24k k22k7 2k14 将x x  ， 4 代入，解得x  ，················13分 1 2 k23 xx  0 4k3 1 2 k23 2k14  1 9k12 【将x  代入y2kx 中，解得y  ， 0 4k3  2 0 68k 消去k，得到点S的轨迹为定直线l :3x4y60 上的一段 1 线段（不含线段端点S,S ）．·····························································14分】 1 2 2k14 【将x  化为2k(2x 1)3x 14， 0 4k3 0 0  1 将S的坐标x ,y 代入y2kx 中，并化为2k(2x 1)4(y 2)， 0 0  2 0 0 故3x 144(y 2)，即点S的轨迹为定直线l :3x4y60 上的一段 0 0 1 线段（不含线段端点S,S ）．·····························································14分】 1 2 3 因为M(1,0)，F(2,0)，且|SM |2 |SF|213，记H( ,0)， 2  1 5 所以|SM |2 |SF|22|SH |2   13，故|SH | ，即S的轨迹方程为  4 2 3 25 5 (x )2  y2  ，表示以点H 为圆心，半径为 的圆H ，······················15分 2 4 2 3 设直线l 与y轴，x轴分别交于S (0, ),S (2,0)，依次作出直线TS ,TS,TS ,TS ， 1 3 2 4 3 1 2 4 14 4 且四条直线的斜率分别为：k 7，k  ，k  3，k  ， TS3 TS1 3 TS2 TS4 3 因为k k k k ，所以线段SS 是线段S S 的一部分.······················· 16分 TS3 TS1 TS2 TS4 1 2 3 4 3 经检验点S (0, ),S (2,0)均在圆H 内部，所以线段S S 也必在圆H 内部，因此线 3 2 4 3 4     段SS 也必在圆H 内部，所以满足条件TPSQPSTQ的点S始终在圆H 内部， 1 2     故不存在这样的点S，使得TPSQPSTQ，且|SM |2 |SF|213成立．····17分 解法二：（3）若直线l斜率不存在，此时直线l与双曲线右支无交点，不合题意， 不满足条件，故直线l斜率存在，··························································· 9分  y2 x2 1  1  3 设直线l方程y2kx ，联立方程，得 ，化简整理，得  2  y2k  x 1     2 高三数学试题 第15页（共8页） {#{QQABDY4QgggAAAAAAAhCAwVqCAKQkAEACAoGwFAMsAABCBFABAA=}#} 0  3k2 0   3k2 x2   k2 4k  x   1 k2 2k7   0，则    k k 2 2   4 3 k 0 ，···············10分 4   1 k22k7 4 0   k23 1 1 因为 k22k7 k4230恒成立，所以k230，故k24k 0， 4 4 14 解得: k  3，·········································································11分 3     TP SP TP SP 由TPSQPSTQ，得  ，且SPQ，假设  ，则 TQ SQ TQ SQ 1 x x  1 2   P  T  T  Q  ，  P  S    S  Q  ，设Px,y ，Qx ,y ，Sx ,y ，则   2 1 ， 1 1 2 2 0 0  2 y 1 y 2  1  1 x x  (1) 即 1 2 2 ，·······································································12分  y y 2(1) 1 2  x x x  1 2   0 1 x x x (1) 又 ，所以 1 2 0 ，  y  y 1 y 2 y 1 y 2 y 0 (1)  0 1  y2  y2 x2  1 1 x2  1 1  1 3  1 3 联立方程 ，得 ，两式相减，得  y 2  2y 2 x 2  2 1 2x 2  2 2  2 3  2 3 1 (x x )(x x ) (y y )(y y )12，将上述等式代入，得 1 2 1 2 3 1 2 1 2 1 1 x (1) (1) y (1)2(1)(1)(1)，·····························13分 0 2 3 0 1 2 即 x  y 1，亦即3x 4y 60，故点S为定直线l :3x4y60 上的 2 0 3 0 0 0 1 一段线段（挖掉左右端点S,S ）．··························································14分 1 2 以下同解法一． 高三数学试题 第16页（共8页） {#{QQABDY4QgggAAAAAAAhCAwVqCAKQkAEACAoGwFAMsAABCBFABAA=}#}