文档内容
玉溪师范学院附属中学 2024-2025 学年高三上学期开学适应性考试
数学
考试范围:高考范围;考试时间:120分钟
第I卷(选择题)
一、单选题(每小题5分,共8小题,共计40分)
1.已知集合 ,若 ,则所有 的取值构成的集合为( )
A. B. C. D.
2.已知复数 ( 为虚数单位),则 ( )
A.8 B.9 C.10 D.100
3.某公司对员工的工作绩效进行评估,得到一组数据 ,后来复查数据时,又将 重复记
录在数据中,则这组新的数据和原来的数据相比,一定不会改变的是( )
A.平均数 B.中位数 C.极差 D.众数
4.函数 的图象大致为( )
A. B.
C. D.
5. 是抛物线 上的两点, 为坐标原点.若 ,且 的面积为 ,则
( )
A. B. C. D.
6.已知向量 以 为基底时的坐标为 ,则 以 为基底时的坐标为(
)A. B. C. D.
7.若" "为假命题,则 的取值范围为( )
A. B. C. D.
8.已知函数 ,若关于 的方程 有两个不等
实根 ,且 ,则 的最大值是( )
A. B. C. D.
二、多选题(每小题6分,共3小题,选对得部分分,选错得0分,共计18分)
9.在 的展开式中,下列命题正确的是( )
A.偶数项的二项式系数之和为32
B.第3项的二项式系数最大
C.常数项为60
D.有理项的个数为3
10.已知椭圆 的左、右焦点分别为 ,左、右顶点分别为 是 上异于
的一个动点.若 ,则下列说法正确的有( )
A.椭圆 的离心率为
B.若 ,则
C.直线 的斜率与直线 的斜率之积等于
D.符合条件 的点 有且仅有2个
11.已知函数 的定义域为 ,则( )A. B.函数 是奇函数
C. D. 的一个周期为3
第II卷(非选择题)
三、填空题(每小题5分,共3小题,共计15分)
12.某省的高中数学学业水平考试,分为 五个等级,其中 等级的比例为 .假设
某次数学学业水平考试成绩服从正态分布 ,其中王同学得分88分等级为 ,李同学得分85分
等级为 .请写出一个符合条件的 值__________.
(参考数据:若 ,则 ,
13.有甲、乙两个工厂生产同一型号的产品,其中甲厂生产的占 ,甲厂生产的次品率为 ,乙厂生产
的占 ,乙厂生产的次品率为 ,从中任取一件产品是次品的概率是__________.
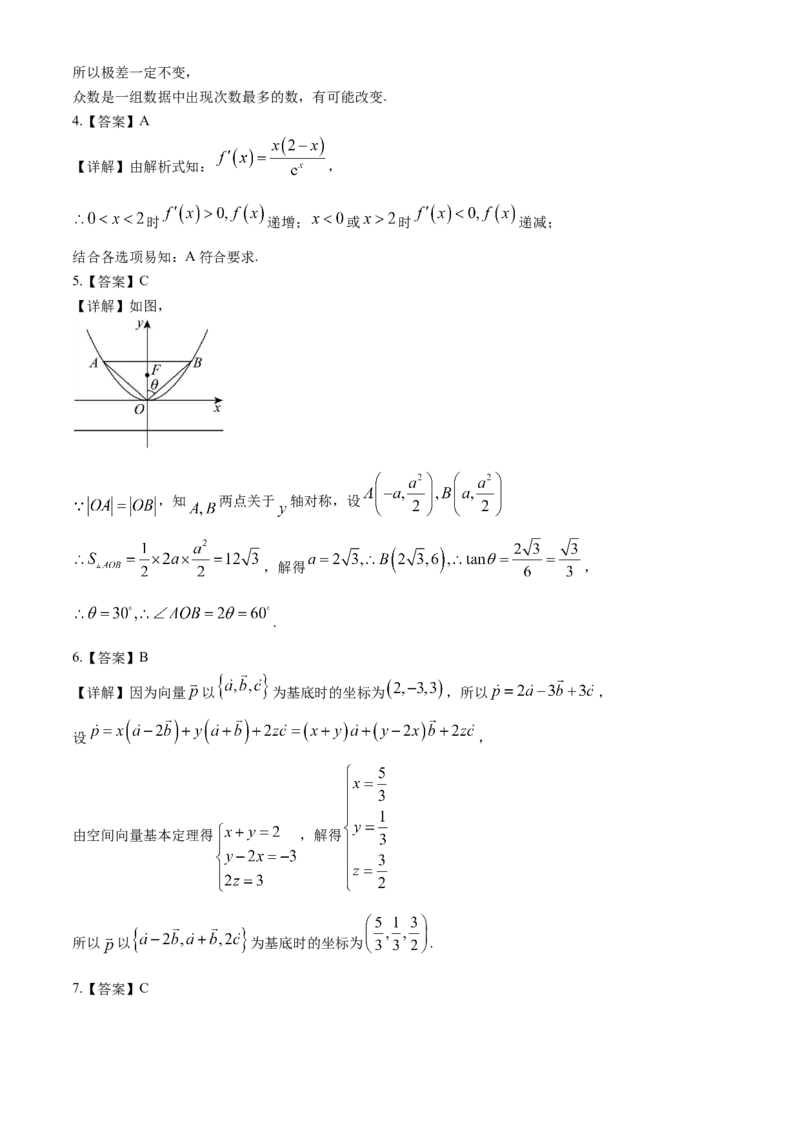
14.已知函数 的部分图象如图所示.若在 中,
,则 面积的最大值为__________.
四、解答题(15题13分,16、17题各15分,18、19题各17分,共计77分)
15.已知等差数列 ,若 ,且 成等比数列.
(1)求数列 的通项公式;
(2)若 ,设 ,求数列 的前 项和 .
16.2021年某公司为了提升一项产品的竞争力和市场占有率,对该项产品进行了科技创新和市场开发,经
过一段时间的运营后,统计得到 之间的五组数据如下表:1 2 3 4 5
9 11 14 26 20
其中, (单位:百万元)是科技创新和市场开发的总投入, (单位:百万元)是科技创新和市场开发
后的收益.
(1)求相关系数 的大小(精确到0.01),并判断科技创新和市场开发后的收益 与科技创新和市场开发
的总投入 的线性相关程度;
(2)该公司对该产品的满意程度进行了调研,在调研100名男女消费者中,得到的数据如下表:
满意 不满意 总计
男 45 10 55
女 25 20 45
总计 70 30 100
是否有 的把握认为消费者满意程度与性别有关?
(3)对(2)中调研的45名女消费者,按照其满意程度进行分层抽样,从中抽出9名女消费者到公司进行
现场考察,再从这9名女消费者中随机抽取4人进行深度调研,设这4人中选择“满意”的人数为 ,求
的分布列及数学期望.
参考公式:① ;
② ,其中 .
临界值表:
0.100 0.050 0.025 0.010 0.001
2.706 3.841 5.024 6.635 10.828
参考数据: .
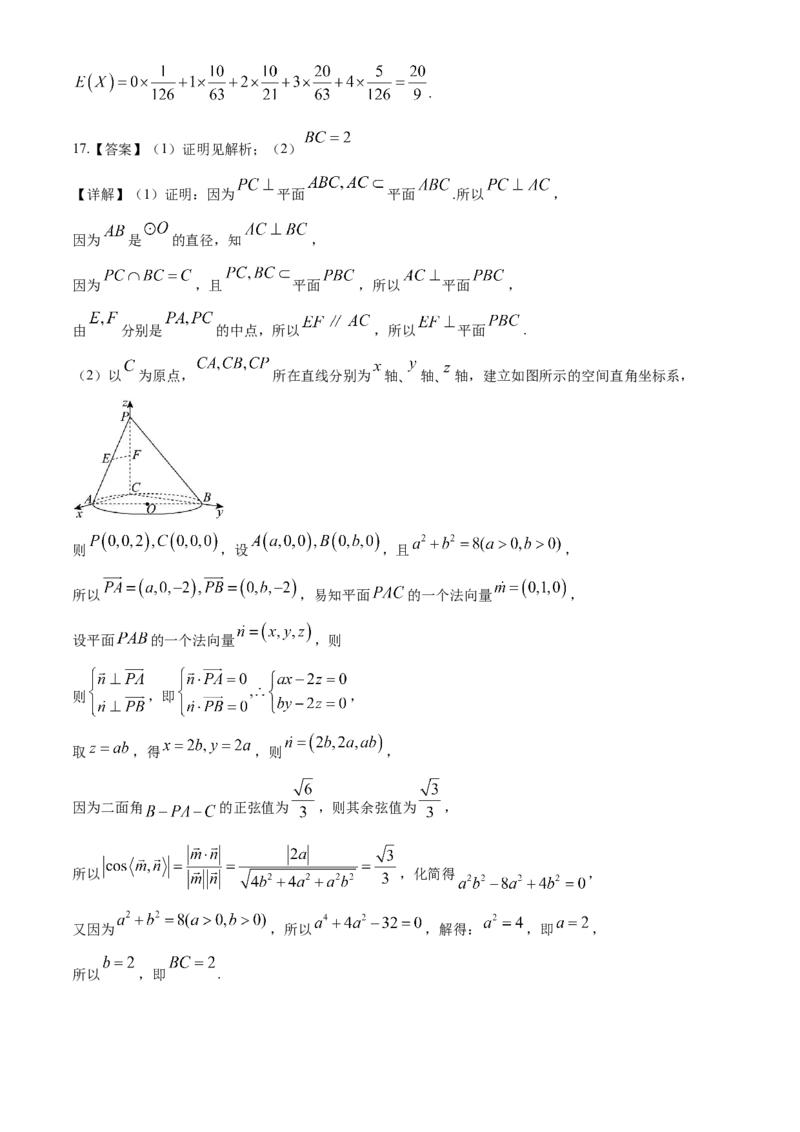
17.如图所示, 是 的直径,点 是 上异于 平面 分别为 , 的中点,(1)求证: 平面 ;
(2)若 ,二面角 的正弦值为 ,求 .
18.已知双曲线 的渐近线方程为 ,左焦点为F,过 的直线为 ,
原点到直线 的距离是 .
(1)求双曲线的方程;
(2)已知直线 交双曲线于不同的两点 ,问是否存在实数 ,使得以 为直径的圆经过
双曲线的左焦点 .若存在,求出 的值;若不存在,请说明理由.
19.设实系数一元二次方程 ①,有两根 ,则方程可变形为
,展开得 ②,
比较①②可以得到
这表明,任何一个一元二次方程的根与系数的关系为:两个根的和等于一次项系数与二次项系数的比的相
反数,两个根的积等于常数项与二次项系数的比.这就是我们熟知的一元二次方程的韦达定理.
事实上,与二次方程类似,一元三次方程也有韦达定理.
设方程 有三个根 ,则有 ③
(1)证明公式③,即一元三次方程的韦达定理;
(2)已知函数 恰有两个零点.
(i)求证: 的其中一个零点大于0,另一个零点大于-2且小于0;
(ii)求 的取值范围.玉溪师范学院附属中学 2024-2025 学年高三上学期开学适应性考试
数学 答案
考试范围:高考范围;考试时间:120分钟
第I卷(选择题)
一、单选题(每小题5分,共8小题,共计40分)
1.【答案】C
【详解】 ,故当 时,易求 ;
当 时,由 得, 或2.综上得:
2.【答案】C
【详解】 ,所以
3.【答案】C
【详解】平均数是所有数据之和再除以这组数据的个数,故平均数有可能改变,
中位数是按照顺序排列的一组数据中居于中间位置的数,故中位数也可能改变,
极差表示一组数据中最大值与最小值之差,将 重复记录在数据中,最大值与最小值并未改变,所以极差一定不变,
众数是一组数据中出现次数最多的数,有可能改变.
4.【答案】A
【详解】由解析式知: ,
时 递增; 或 时 递减;
结合各选项易知:A符合要求.
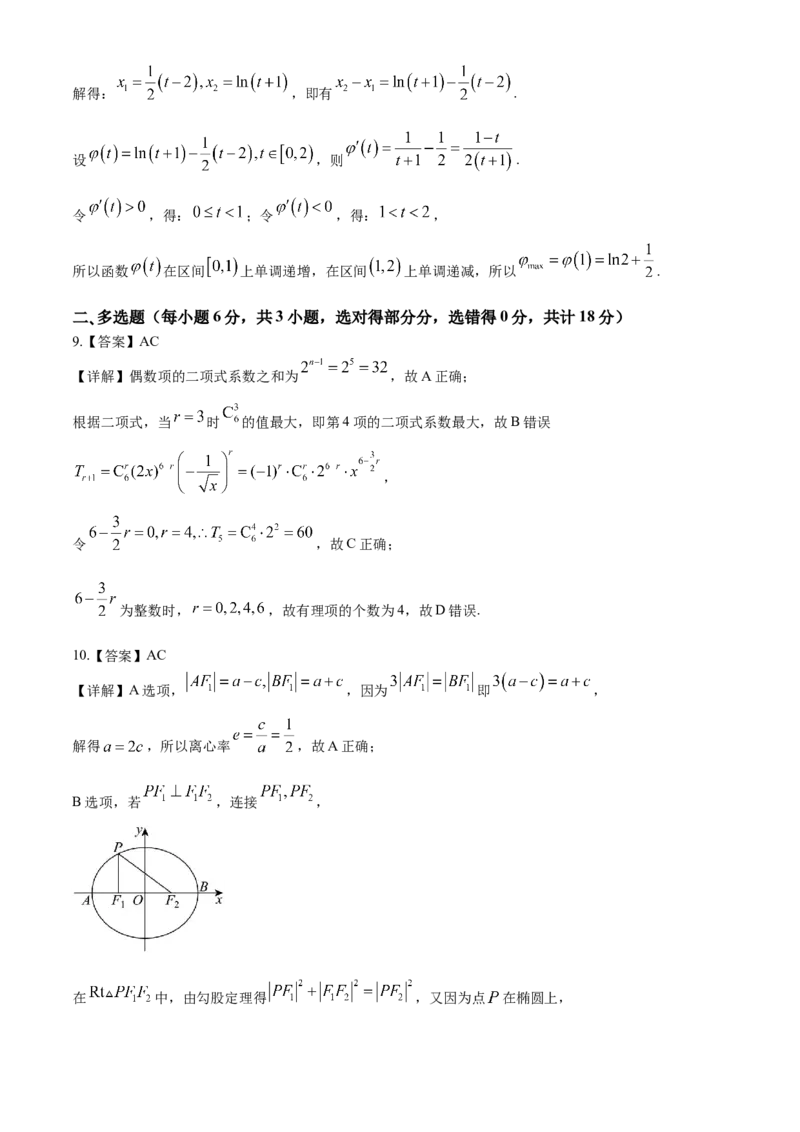
5.【答案】C
【详解】如图,
,知 两点关于 轴对称,设
,解得 ,
.
6.【答案】B
【详解】因为向量 以 为基底时的坐标为 ,所以 ,
设 ,
由空间向量基本定理得 ,解得
所以 以 为基底时的坐标为 .
7.【答案】C【详解】由题意得该命题的否定为真命题,即" "为真命题,
即 ,
令 ,因为 ,则 ,则存在 ,使得 成立,
令 ,令 ,则 (负舍),
则根据对勾函数的性质知 在 上单调递减,在 上单调递增,
且 ,则 ,则 .
8.【答案】B
【详解】由 可得:
函数 的定义域为 ,
所以函数 在 上单调递增.
令 .
因为关于 的方程 有两个不等实根 ,
则关于 的方程 有两个不等实根 .
作出函数 的图象,如图所示:
所以结合图形可知 .
由 可得: ,解得: ,即有 .
设 ,则 .
令 ,得: ;令 ,得: ,
所以函数 在区间 上单调递增,在区间 上单调递减,所以 .
二、多选题(每小题6分,共3小题,选对得部分分,选错得0分,共计18分)
9.【答案】AC
【详解】偶数项的二项式系数之和为 ,故A正确;
根据二项式,当 时 的值最大,即第4项的二项式系数最大,故B错误
,
令 ,故C正确;
为整数时, ,故有理项的个数为4,故D错误.
10.【答案】AC
【详解】A选项, ,因为 即 ,
解得 ,所以离心率 ,故A正确;
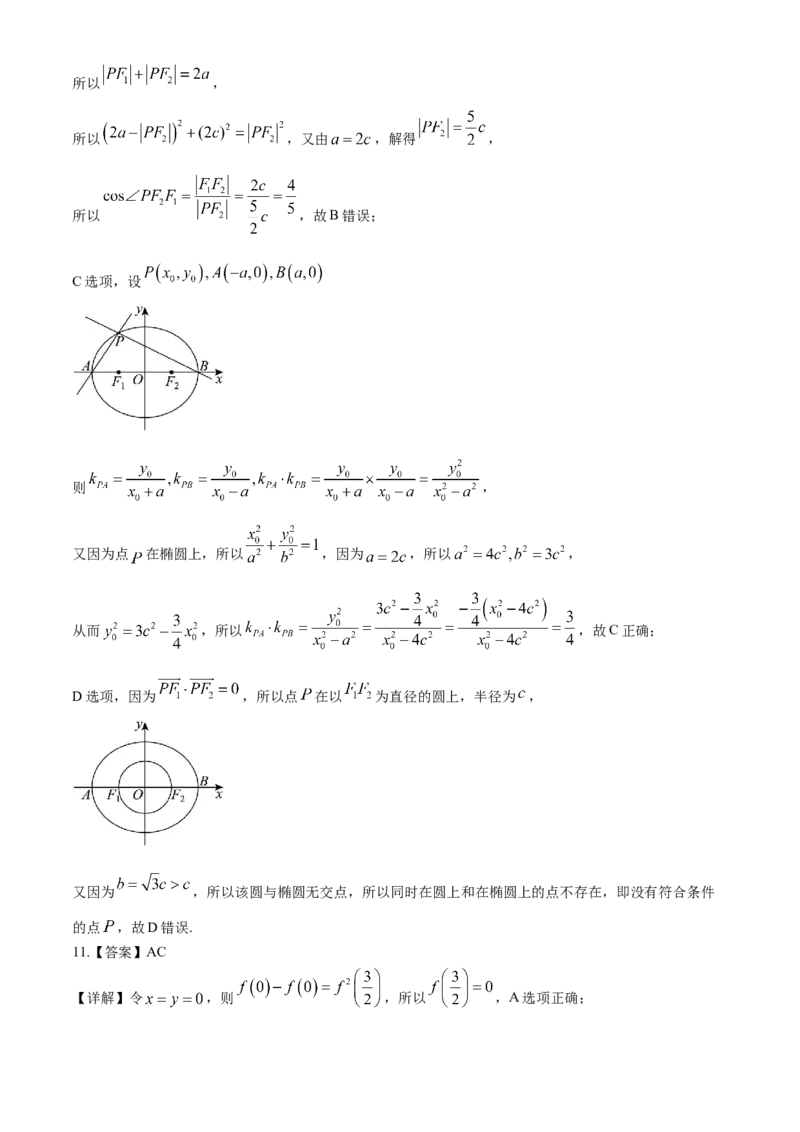
B选项,若 ,连接 ,
在 中,由勾股定理得 ,又因为点 在椭圆上,所以 ,
所以 ,又由 ,解得 ,
所以 ,故B错误;
C选项,设
则 ,
又因为点 在椭圆上,所以 ,因为 ,所以 ,
从而 ,所以 ,故C正确;
D选项,因为 ,所以点 在以 为直径的圆上,半径为 ,
又因为 ,所以该圆与椭圆无交点,所以同时在圆上和在椭圆上的点不存在,即没有符合条件
的点 ,故D错误.
11.【答案】AC
【详解】令 ,则 ,所以 ,A选项正确;令 ,则 ,即 ,所以 是偶函数,B选项
错误;
,令 ,则 ,
令 ,则 ,所以 ,
所以 ,因为 ,所以 ,C选项正确;
令 ,则 ,
所以 ,所以 的一个周
期为 选D项错误.
第II卷(非选择题)
三、填空题(每小题5分,共3小题,共计15分)
12.【答案】7(答案不唯一,只需要填区间[5,8]内的任意一个值)
【详解】由题意可知, ,解得 .
故答案为:7(答案不唯一,只需要填区间 内的任意一个值).
13.【答案】
【详解】设 为甲,乙两厂生产的产品, 表示取得次品,
,
所以 .
所以任取1件产品的概率为0.026.
14.【答案】
【详解】由图象可得 ,解得 ,所以 ,由 ,由图 ,即 ,
由 ,得 .故 ,
在 中, ,
,即 ,
设角 的对边为 ,由 ,
则 ,
,当且仅当 时等号成立.
,所以 面积最大值为 .
四、解答题(15题13分,16、17题各15分,18、19题各17分,共计77分)
15.【答案】(1) 或 (2)
【详解】解:(1) ①
成等比数列, 化简得 ,若
若 ②,由①②可得,
所以数列的通项公式是 或
(2)由(1)得
16.【答案】(1)0.84,科技创新和市场开发后的收益 与科技创新和市场开发的总投入 具有较强的相关性.(2)有;(3)分布列见解析,
【详解】(1)由题意可得 ,
,
,
.
"科技创新和市场开发后的收益 与科技创新和市场开发的总投入 具有较强的相关性.
(2)由题意:
满意 不满意 总计
男 45 10 55
女 25 20 45
总计 70 30 100
,
有 的把握认为消费者满意程度与性别有关.
(3)易知9人中满意的有5人,不满意的有4人
由题意可知, 的可能取值为 ,
,
的分布列为:
0 1 2 3 4.
17.【答案】(1)证明见解析;(2)
【详解】(1)证明:因为 平面 平面 .所以 ,
因为 是 的直径,知 ,
因为 ,且 平面 ,所以 平面 ,
由 分别是 的中点,所以 ,所以 平面 .
(2)以 为原点, 所在直线分别为 轴、 轴、 轴,建立如图所示的空间直角坐标系,
则 ,设 ,且 ,
所以 ,易知平面 的一个法向量 ,
设平面 的一个法向量 ,则
则 ,即 ,
取 ,得 ,则 ,
因为二面角 的正弦值为 ,则其余弦值为 ,
所以 ,化简得 ,
又因为 ,所以 ,解得: ,即 ,
所以 ,即 .18.【答案】(1) .(2) .
【详解】试题分析:(1) ,
原点到直线 的距离, .
.故所求双曲线方程为 .
(2)把 代入 中消去 ,整理得 .
设 ,则 ,
因为以CD为直径的圆经过双曲线的左焦点F,所以 ,
可得 把 代入,
解得:
解 ,得 满足
19.【答案】(1)证明见解析;(2)(i)证明见解析;(ii) .
【详解】(1)证明:因为方程 有三个根 ,
所以方程 即为 ,
变形为 ,
比较两个方程可得 .
(2)(i)证明: 有两个零点, 有一个二重根 ,一个一重根 ,且由(1)可得 ,由 可得 .
由 可得 .
联立上两式可得 ,解得 ,
又 ,综上 .
(ii)解:由(i)可得 ,
.
令 ,则 ,
,当 时, ,
在 上单调递增, ,
.