文档内容
韶关市 2024 届高三综合测试(二)
数学
本试卷共 4页,19小题,满分 150分,考试时间 120分钟.
注意事项:
1.答卷前、考生务必用黑色字迹的钢笔或签字笔将自己的姓名、准考证号、学校和班级填写在
答题卡上,将条形码横贴在答题卡右上角“条形码粘贴处”.
2.作答选择题时,选出每小题答案后,用 2B 铅笔把答题卡对应题目选项的答案信息点涂黑;
如需改动,用橡皮擦干净后,再选涂其他答案.答案不能答在试卷上.
3.非选择题必须用黑色字迹的钢笔或签字笔作答,答案必须写在答题卡各题目指定区城内和应
位置上;如需改动,先划掉原来的答案,然后再写上新答案;不准使用铅笔和涂改液,不按以
上要求作答无效.
4.考生必须保持答题卡的整洁.考试结束后,将试卷和答题卡一并交回。
一、选择题:本题共 8小题,每小题 5分,共 40分.在每小题给出的四个选项中,只有一项是
符合题目要求的.
{ } 1 ( )
1.若集合A= x1< x ≤6 ,B = x <0,则 A B =( )
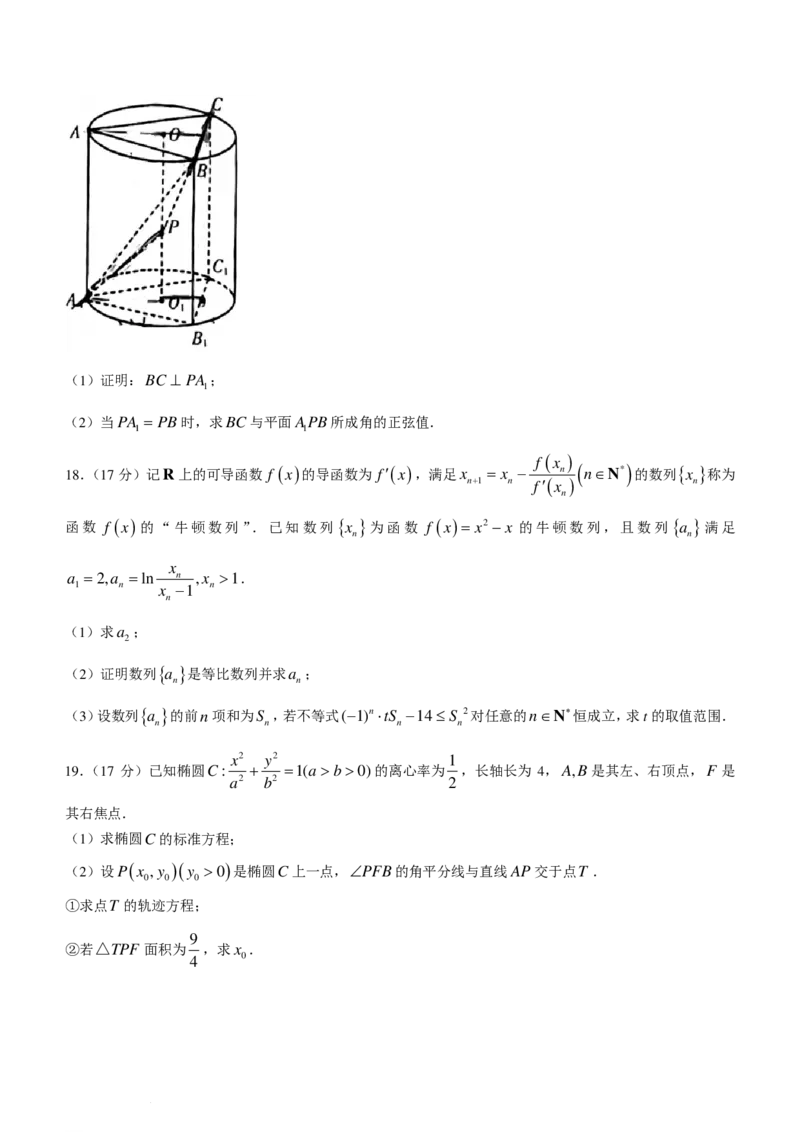
x−7 R
A. { x x ≤1或6≤ x ≤7 } B. { x x ≤1或6< x<7 }
C. { x x<1或6≤ x<7 } D. { x x ≤1或6< x ≤7 }
2.设α,β,γ是三个不同的平面,m,l 是两条不同的直线,则下列命题正确的是( )
A.若m∥α,m∥β,则α∥β B.若m∥α,l∥α,则m∥l
C.若m ⊥α,m ⊥β,则α∥β D.若α⊥γ,β⊥γ,则α∥β
3.已知一组数据:12,16,22,24,25,31,33,35,45,若去掉 12 和 45,将剩下的数据与原数据相比,
则( )
A.极差不变 B.平均数不变 C.方差不变 D.上四分位数不变
4 . 过 点 P (−2,3 ) 作 斜 率 为 −2 的 直 线 , 若 光 线 沿 该 直 线 传播 经 x 轴 反 射 后 与 圆
C:(x−3)2 +(y−2)2 = r2(r >0)相切,则r =( )
A. 2 B. 3 C.2 D. 5
5.在工程中估算平整一块矩形场地的工程量 W(单位:平方米)的计算公式是W =(长+4 )×(宽+4 ) ,在
不测量长和宽的情况下,若只知道这块矩形场地的面积是10000平方米,每平方米收费1元,请估算平整完这
块场地所需的最少费用(单位:元)是( )
学科网(北京)股份有限公司A.10000 B.10480 C.10816 D.10818
1 3
6.在△ABC 中,tanA= ,tanB = .若△ABC 的展长边的长为 17 .则最短边的长为( )
4 5
A. 2 B. 3 C.2 D. 5
x2 y2
7.已知双曲线C: − =1(a >0,b>0)的左焦点为F ,过点F 的直线l:3x+4y+m =0与 y轴交于点
a2 b2
B,与双曲线C交于点A(A在y轴右侧).若B是线段AF 的中点,则双曲线C的渐近线方程为( )
3 1
A.y =± x B.y = ± x C. y = ± 3x D. y = ±2x
3 2
a,a ≥b b,a ≥b
8 . 定 义 max { a,b }= ,min { a,b }= , 对 于 任 意 实 数 x >0,y >0 , 则
b,a1.
1 n x −1 n
n
(1)求a ;
2
(2)证明数列{ a }是等比数列并求a ;
n n
(3)设数列{ a }的前n项和为S ,若不等式(−1)n⋅tS −14≤ S 2对任意的n∈N∗恒成立,求t的取值范围.
n n n n
x2 y2 1
19.(17 分)已知椭圆C: + =1(a >b>0)的离心率为 ,长轴长为 4,A,B是其左、右顶点,F 是
a2 b2 2
其右焦点.
(1)求椭圆C的标准方程;
(2)设P ( x ,y )( y >0 )是椭圆C上一点,∠PFB的角平分线与直线AP交于点T .
0 0 0
①求点T 的轨迹方程;
9
②若△TPF 面积为 ,求x .
4 0
学科网(北京)股份有限公司