文档内容
石嘴山三中2024届高三一模考试数学(文科)试题答案
一.单选题 ACDADB CDABDB
二.填空题 3, , ②③⑤
,
三.答案详解
1.已知集合 , ,则 ( )
A. B. C. D.
【答案】A
【分析】根据题意求解 ,再求解 ,确定选项.
【详解】因为 ,
所以 .
2.设 在复平面内对应的点为 ,则 在复平面内对应的点为( )
A. B. C. D.
【答案】C
【分析】利用复数运算法则化简 即可求解.
【详解】依题意得 ,
所以 ,
则 在复平面内对应的点为 .
故选:C
3.采购经理指数(PMI),是通过对企业采购经理的月度调查结果统计汇总、编制而
第 页 共 页
学科网(北京)股份有限公司
1 25成的指数,它涵盖了企业采购、生产、流通等各个环节,包括制造业和非制造业领
域,是国际上通用的检测宏观经济走势的先行指数之一,具有较强的预测、预警作
用.制造业PMI高于 时,反映制造业较上月扩张;低于 ,则反映制造业较
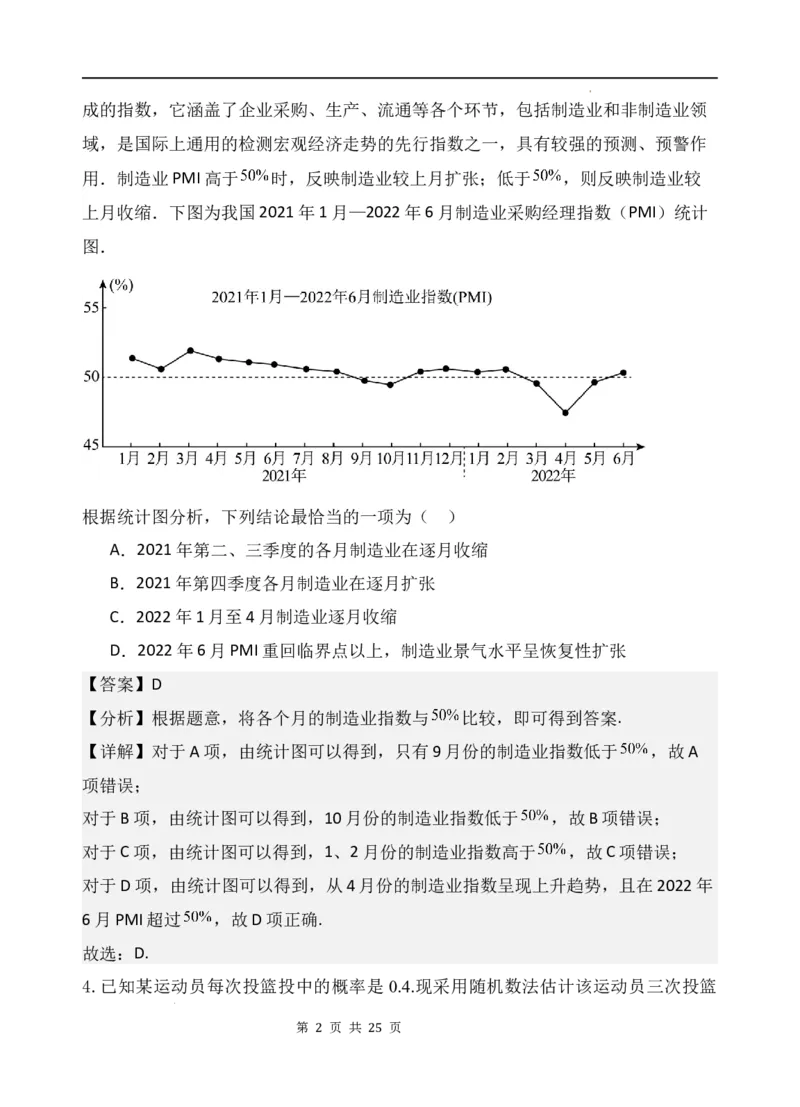
上月收缩.下图为我国2021年1月—2022年6月制造业采购经理指数(PMI)统计
图.
根据统计图分析,下列结论最恰当的一项为( )
A.2021年第二、三季度的各月制造业在逐月收缩
B.2021年第四季度各月制造业在逐月扩张
C.2022年1月至4月制造业逐月收缩
D.2022年6月PMI重回临界点以上,制造业景气水平呈恢复性扩张
【答案】D
【分析】根据题意,将各个月的制造业指数与 比较,即可得到答案.
【详解】对于A项,由统计图可以得到,只有9月份的制造业指数低于 ,故A
项错误;
对于B项,由统计图可以得到,10月份的制造业指数低于 ,故B项错误;
对于C项,由统计图可以得到,1、2月份的制造业指数高于 ,故C项错误;
对于D项,由统计图可以得到,从4月份的制造业指数呈现上升趋势,且在2022年
6月PMI超过 ,故D项正确.
故选:D.
4.已知某运动员每次投篮投中的概率是 0.4.现采用随机数法估计该运动员三次投篮
第 页 共 页
学科网(北京)股份有限公司
2 25中,恰有两次投中的概率:先由计算器随机产生0~9中的整数,指定1,2,3,4
表示投中,5,6,7,8,9,0表示未投中;再以每三个随机数为一组,代表三次投
篮的结果.现产生了如下 10组随机数:907 966 191 925 271 431 932 458 569 683.估
计该运动员三次投篮恰有两次投中的概率为( A )
A. B. C. D.
5.已知函数 是定义域为 的偶函数,在区间 上单调递增,且对任意
,均有 成立,则下列函数中符合条件的是( )
A. B. C. D.
【答案】D
【分析】由指数、对数运算性质结合函数单调性、奇偶性定义逐一判断每个选项即
可求解.
【详解】对于A, ,故A错误;
对于B, ,故 不是偶函数,故B错误;
对于C, ,故C错误;
对于D, ,
又 定义域为全体实数,它关于原点对称,且 ,
即函数 是定义域为 的偶函数,
当 时, 单调递增,满足题意.
故选:D.
6已知平行四边形 ABCD的三个顶点为 A(-1,2),B(3,4),C(4,-2),点
第 页 共 页
学科网(北京)股份有限公司
3 25(x,y)在平行四边形ABCD的内部,则z=2x-5y的取值范围是( B)
A(-14,16) B(-14,20) C(-12,18) D(-12,20)
7.正方体 中, 为 的中点,则直线 与 所成角的正切值为
( )
A. B. C. D.1
【答案】C
【分析】平移直线 到 ,将直线DP与 所成的角转化为DP与 所成的
角,利用几何求法求解即可.
【详解】
连接 ,根据正方体的性质可知 ,
所以 或其补角为直线 DP与 所成的角,
因为 平面 , ⊂平面 ,所以 又 ,
, ⊂平面 ,所以 平面
又 平面 ,所以
设正方体的棱长为2,则
第 页 共 页
学科网(北京)股份有限公司
4 25在 中, 所以 故直线 与 所成的角的
正切值为 .
故选: C.
8.已知函数 (其中 )图象的一个对称中心为 ,为了得到
的图象,只需将 的图象( )
A.向左平移 个单位 B.向左平移 个单位
C.向右平移 个单位 D.向右平移 个单位
【答案】D
【分析】根据题意,利用正弦型函数的性质求得 ,再结合三角函
数的图像变换,即可求解.
【详解】因为函数 的一个对称中心为 ,且 ,
将点 代入 ,可得 ,解得 ,
所以 ,可得 ,
第 页 共 页
学科网(北京)股份有限公司
5 25所以函数 的图象向右平移 个单位可得到 的图象.
故选:D.
9.如图,在 中, , 为 上一点,且 ,若
,则 的值为( )
A. B. C. D.
【答案】A
【分析】结合题意可知 三点共线,进而得到 ,利用向量基本定理表示出
,进而表示出 计算即可.
【详解】因为 ,所以
所以 ,
因为 ,所以 ,
即 ,
第 页 共 页
学科网(北京)股份有限公司
6 25因为 三点共线,所以 ,解得 ,
所以 ,
而 ,
所以 ,
即 .
10.已知数列 满足 ,设其前 项和为 ,则
( )
A.2500 B.2600 C.2700 D.2800
【答案】B
【分析】由分组求和法以及等差数列求和公式即可求解.
【详解】若 ,则 ,
若 ,则 ,
所以数列 的偶数项构成以2为首项,公差为2的等差数列,奇数项构成常数数
列,
.
故选:B.
11.已知 , , ,则a,b,c( )
A. B. C. D.
第 页 共 页
学科网(北京)股份有限公司
7 25【答案】D
【分析】根据给定条件,构造函数,利用导数探讨单调性即可比较大小.
【详解】令 ,求导得 ,
当 时, ,则 在 上单调递减,
则 ,即 ,而 ,于是 ,
所以 .
故选:D
12.已知 分别是椭圆 的左、右焦点, 在 上, 在 轴
上, ,以 为直径的圆过 ,且 的面积为 ,则椭圆 的标准
方程为( )
A. B.
C. D.
【答案】B
【分析】设 ,表示出 的面积,结合向量关系以及垂直关系,
求出点 ,借助椭圆的定义求解即可.
第 页 共 页
学科网(北京)股份有限公司
8 25【详解】
结合题意可得: , ,设 ,
则由 的面积为 ,得 ①,
由 ,得 ②.
连接 以 为直径的圆过 , ③.
由②③得 ,
结合①得 ,
,
,故椭圆 的标准方程为 ,
故选:B.
二、填空题(本大题共4小题,每小题5分,共20分)
13.在各项均为正数的等比数列 中, ,则 .
【答案】3
【分析】利用等比数列的性质,结合对数运算性质求解即可.
第 页 共 页
学科网(北京)股份有限公司
9 25【详解】解: .
故答案为:3
14.已知正四棱锥的底面边长为2,高为4,它的所有顶点都在同一球面上,则这个
球表
面积是 ___ __
15.已知双曲线 的左焦点为 ,过 作一倾斜角为 的直线交双曲线右支
于 点,且满足 ( 为原点)为等腰三角形,则该双曲线的离心率 为
.
【答案】 /
【分析】画出图形利用双曲线定义并根据 为等腰三角形可得 ,再
由勾股定理可得 ,即求出离心率.
【详解】如图,连接 ,
第 页 共 页
学科网(北京)股份有限公司
10 25因为P在双曲线的右支上,则 ,又易知双曲线 的左焦点
,
又因为 为等腰三角形, ,可知 ,
可得 ,即 ,又 ,
即 为等边三角形,即 , ,
所以 ,
所以在直角 中, , ,则 ,
所以 ,即 ,
解得 .
故答案为:
16.下列命题中:
①若集合 中只有一个元素,则 ;
②已知命题p: , ,如果命题p是假命题,则实数a的取值范围是
;
③已知函数 的定义域为 ,则函数 的定义域为 ;
第 页 共 页
学科网(北京)股份有限公司
11 25④函数 在 上单调递增;
⑤方程 的实根的个数是2.
所有正确命题的序号是 .
【答案】②③⑤
【分析】利用判别式可判断①;利用特称命题的否定为全称命题可判断②;求出
的定义域可判断③;分离常量后根据反比例函数的单调性可判断④;在同一坐
标系中作出 和 的图象可判断⑤.
【详解】对于①: 时, ; 时, ,则 ,故 或
1,
故错误;
对于②:p: , 为假命题,则 , 为真命题,
故 即 ,故正确;
对于③: ,则 ,即 的定义域为 ,故正确;
对于④: ,其在 上单调递减,故错误;
对于⑤:在同一坐标系中作出 和 的图象,观察两图象有2个交
点,
则方程 的实根的个数是2,故正确.
第 页 共 页
学科网(北京)股份有限公司
12 25故答案为:②③⑤.
三、解答题(共70分)解答应写出文字说明、证明过程或演算步骤.第17~21题为必
考题,每个试题考生都必须作答.第22、23题为选考题,考生根据要求作答.
17.足球是世界普及率最高的运动,我国大力发展校园足球.为了解本地区足球特色
学校的发展状况,社会调查小组得到如下统计数据:
年份x 2014 2015 2016 2017 2018
足球特色学校y(百个) 0.30 0.60 1.00 1.40 1.70
(1)根据上表数据,计算y与x的相关系数r,并说明y与x的线性相关性强弱.
(已知: ,则认为y与x线性相关性很强; ,则认为y与x线
性相关性一般; ,则认为y与x线性相关性较弱):
(2)求y关于x的线性回归方程,并预测A地区2025年足球特色学校的个数(精确到
个).
参考公式和数据: ,
, , .
【答案】(1) ,y与x线性相关性很强
第 页 共 页
学科网(北京)股份有限公司
13 25(2) ;244个
【分析】(1)根据公式求解相关系数r,再根据 判断即可;
(2)先根据公式求得回归方程 ,再代入 求解即可.
【详解】(1)由题得 ,
.
所以 ,
∴y与x线性相关性很强.
(2) ,
,
∴y关于x的线性回归方程是 .当 时,
,
即该地区2025年足球特色学校有424个.
第 页 共 页
学科网(北京)股份有限公司
14 2518.已知函数
(1)求 的单调递增区间;
(2)三角形 的三边a,b,c满足 ,求 的取值范围.
【答案】(1)
(2)
【分析】(1)先利用倍角公式以及两角和差的正弦公式进行化简可得
,然后根据函数的单调性即可求得 的单调递增区间;
(2)根据余弦定理可求得 ,便可知 的取值范围从而求得 的取值范围.
【详解】(1)解:由题意得:
当 时,函数 单调递增,解得:
第 页 共 页
学科网(北京)股份有限公司
15 25的单调递增区间:
(2)由 可知
由余弦定理得:
故可知
∴
又
∴ .
19.如图,在圆锥 中, 是圆 的直径,且 是边长为4的等边三角形,
为圆弧 的两个三等分点, 是 的中点.
第 页 共 页
学科网(北京)股份有限公司
16 25(1)证明: 平面 .
(2)求点 到平面 的距离.
【答案】(1)证明见解析
(2) .
【分析】(1)利用平行四边形对边平行可得 ,再由线面平行判定定理求
证;
(2)利用等体积法求点面距离即可得解.
【详解】(1)证明:取 的中点 ,连接 .
因为 为圆弧 的两个三等分点,所以 .
因为 分别为 的中点,所以 ,
则 ,从而四边形 为平行四边形,
故 .
因为 平面 平面 ,所以 平面 .
(2)作 ,垂足为 ,连接 .
第 页 共 页
学科网(北京)股份有限公司
17 25由 平面 , 平面 ,所以 ,
又 平面 ,所以 平面 .
因为 为圆弧 的两个三等分点,所以 ,则 .
因为 是边长为4的等边三角形,所以 .
因为 是 的中点,所以 ,
则三棱锥 的体积 .
因为 ,所以 ,则 .
设点 到平面 的距离为 ,则三棱锥 的体积 .
因为 ,所以 ,解得 ,
即点 到平面 的距离为 .
.
20.已知抛物线 和圆 ,倾斜角为45°的直线 过 的
焦点且与 相切.
(1)求p的值:
(2)点M在 的准线上,动点A在 上, 在A点处的切线l 交y轴于点B,设
2
第 页 共 页
学科网(北京)股份有限公司
18 25,求证:点N在定直线上,并求该定直线的方程.
【答案】(1) ;
(2)证明见解析,定直线方程为 .
【分析】(1)设直线l 的方程为 ,再根据直线和圆相切求出 的值得解;
1
(2)依题意设 ,求出切线l 的方程和B点坐标,求出 ,
2
,即得证.
【详解】(1)由题得抛物线 的焦点坐标为 ,
设直线l 的方程为 ,
1
由已知得圆 的圆心 ,半径 ,
因为直线l 与圆 相切,
1
所以圆心到直线 的距离 ,
即 ,解得 或 (舍去).
所以 .
(2)依题意设 ,由(1)知抛物线 方程为 ,
第 页 共 页
学科网(北京)股份有限公司
19 25所以 ,所以 ,设A , ),则以A为切点的切线l 的斜率为
2
所以切线l 的方程为 .
2
令 ,即l 交y轴于B点坐标为 ,
2
所以 ,
∴ ,
∴ .
设N点坐标为(x,y),则 ,
所以点N在定直线 上.
21.已知函数 .
(1)当 时,求曲线 在点 处的切线方程.
(2)若 有两个零点,求实数 的取值范围.
【答案】(1) (2)
第 页 共 页
学科网(北京)股份有限公司
20 25【详解】(1)当 时, ,则 ,
,所以 .
故曲线 在点 处的切线方程为 ,即 .
(2)由 有两个零点,
得方程 在 上有两个不同的实数解.
当 时,显然方程没有正实数解,所以 .
则方程 在 上有两个不同的实数解.
令 ,则 .
显然 在 上为减函数,又 ,
所以当 时, ;当 时, .
所以 在 上单调递增,在 上单调递减,且 .
当 时, ;当 时, ,
要使方程 在 上有两个不同的实数解,
则 与 的图象在 上有两个不同的交点,
第 页 共 页
学科网(北京)股份有限公司
21 25结合图象可知 ,解得 ,
综上,实数 的取值范围为 .
(二)选考题:共10分.请考生在第22、23题中任选一题作答.并用2B铅笔将所选
题号涂黑,多涂、错涂、漏涂均不给分.如果多做,则按所做的第一题计分.
22.在直角坐标系xOy中,曲线C的参数方程为 (其中 为参数).以
坐标原点O为极点,x轴正半轴为极轴建立极坐标系,直线l的极坐标方程为
.
(1)求直线l的直角坐标方程和曲线C的普通方程;
(2)已知点 ,直线l与曲线C交于M,N两点,求 的值.
【答案】(1) ,
(2)
【分析】(1)利用极坐标与直角坐标的关系求直线的直角坐标方程;消去参数得到
曲线C的普通方程;
(2)先求出直线的参数方程,代入曲线中,得到韦达定理,再由根与系数的关系求
出结果.
第 页 共 页
学科网(北京)股份有限公司
22 25【详解】(1)将 代入 ,得 ,
所以直线l的直角坐标方程为 .
由曲线C的参数方程为 ,化为 ,
平方相加得曲线C的普通方程为 .
(2)易得点 在直线l上,
由此可得直线l的参数方程为 (其中t为参数),
将其代入曲线C的普通方程中得 ,
设点M对应的参数为 ,点N对应的参数为 ,则 , ,
所以 , 一正一负,
所以 .
23.设函数 的最小值为t
(1)求t的值;
(2)若a,b,c为正实数,且 ,求证: .
第 页 共 页
学科网(北京)股份有限公司
23 25【答案】(1)3;
(2)证明见解析.
【分析】(1)分类讨论去 中的绝对值,转化为分段函数,求出每段函数值的取
值范围,即可求解;
(2)由(1)得 ,利用已知等式有 ,再应用
基本不等式,即可证明结论.
【详解】(1)(1)
当 时, ;当 时, ;
当 时, ,
所以当 时, 取最小值 .
(2)由(1)可知 ,因为 , , 为正实数,
.
当且仅当 ,即 , , 时取等号,
所以 .
第 页 共 页
学科网(北京)股份有限公司
24 25第 页 共 页
学科网(北京)股份有限公司
25 25