文档内容
2024 届高考新结构数学-选择填空强化训练(9)
一、选择题:本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题
目要求的.
1.在一组样本数据 、 、 、 、 、 、 、 不全相等)的散点
图中,若所有的样本点 都在直线 上,则这组样本数据的相关系数为
( )
A. B. C. D.
【答案】C
【解析】因为所有 的样本点都在直线 上,所以相关系数 满足 .
又因为 ,所以 ,所以 .
故选:C.
2.若椭圆 的离心率为 ,则椭圆 的长轴长为( )
A. 6 B. 或 C. D. 或
【答案】D
【解析】当焦点在 轴时,由 ,解得 ,符合题意,此时椭圆 的长轴长为
;
当焦点在 轴时,由 ,解得 ,符合题意,此时椭圆 的长轴长为 .
故选:D.
3.最早的测雨器记载见于南宋数学家秦九韶所著的《数书九章》(1247年).该书第二章为“天时
类”,收录了有关降水量计算的四个例子,分别是“天池测雨”、“圆罂测雨”、“峻积验雪”和
“竹器验雪”.如图“竹器验雪”法是下雪时用一个圆台形的器皿收集雪量(平地降雪厚度 器皿中积
雪体积除以器皿口面积),已知数据如图(注意:单位 ),则平地降雪厚度的近似值为( )
A. B. C. D.
【答案】C
【解析】如图所示,可求得器皿中雪表面的半径为 ,所以平地降雪厚度的近似值为 .
故选:C
4.设 ,若 ,则 ( )
A. 5 B. 6 C. 7 D. 8
【答案】A
【解析】 展开式第 项 ,
∵ ,∴ ,
∴ .
故选:A.
5.某校高三年级800名学生在高三的一次考试中数学成绩近似服从正态分布 ,若某学生
数学成绩为102分,则该学生数学成绩的年级排名大约是( )
( 附 : , ,
)
A. 第18名 B. 第127名 C. 第245名 D. 第546名
【答案】B
【解析】因为成绩 近似服从正态分布 , ,则 ,
且 ,
所以 ,
因此该校数学成绩不低于102分的人数即年级排名大约是 .
故选:B.
6.声音是由于物体的振动产生的能引起听觉的波,我们听到的声音多为复合音.若一个复合音的数学
模型是函数 ,则下列结论正确的是( )
A. 的一个周期为 B. 的最大值为
C. 的图象关于直线 对称 D. 在区间 上有3个零点
【答案】D
【解析】A. ,故A错误;
B. ,当 , 时,取得最大值1, ,当 , 时,
即 , 时,取得最大值 ,所以两个函数不可能同时取得最大值,所以 的最大值
不是 ,故B错误;C. ,所以函数 的图象不
关于直线 对称,故C错误;
D. ,即 , ,
即 或 ,解得: ,
所以函数 在区间 上有3个零点,故D正确.
故选:D
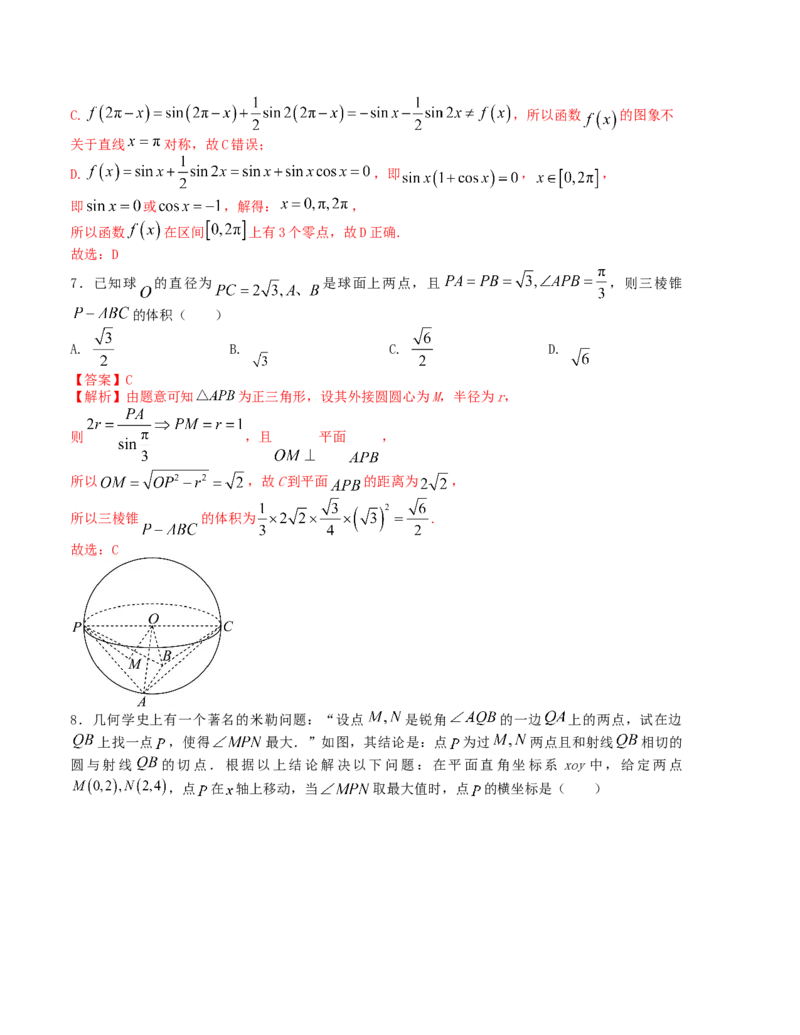
7.已知球 的直径为 是球面上两点,且 ,则三棱锥
的体积( )
A. B. C. D.
【答案】C
【解析】由题意可知 为正三角形,设其外接圆圆心为M,半径为r,
则 ,且 平面 ,
所以 ,故C到平面 的距离为 ,
所以三棱锥 的体积为 .
故选:C
8.几何学史上有一个著名的米勒问题:“设点 是锐角 的一边 上的两点,试在边
上找一点 ,使得 最大.”如图,其结论是:点 为过 两点且和射线 相切的
圆与射线 的切点.根据以上结论解决以下问题:在平面直角坐标系 xoy中,给定两点
,点 在 轴上移动,当 取最大值时,点 的横坐标是( )A. 2 B. 6 C. 2或6 D. 1或3
【答案】A
【解析】由题意知,点 为过 , 两点且和 轴相切的圆与 轴的切点,
已知 ,则线段 的中点坐标为 ,直线 斜率为 ,
线段 的垂直平分线方程为 ,即 .
所以以线段 为弦的圆的圆心在直线 上,
所以可设圆心坐标为 ,
又因为圆与 轴相切,所以圆 的半径 ,又因为 ,
所以 ,解得 或 ,
即切点分别为 和 ,两圆半径分别为 .
由于圆上以线段 (定长)为弦所对的圆周角会随着半径增大而圆周角角度减小,
且过点 的圆的半径比过 的圆的半径大,
所以 ,故点 为所求,
所以当 取最大值时,点 的横坐标是 .
故选:A.
二、选择题:本题共3小题,每小题6分,共18分.在每小题给出的选项中,有多项符合题目要求.全
部选对的得6分,部分选对的得部分分,有选错的得0分.
9.已知复数 , , ,则( )
A. B. 的实部依次成等比数列
C. D. 的虚部依次成等差数列
【答案】ABC
【解析】因为 , ,所以 ,所
以 ,故A正确;因为 , , 的实部分别为1,3,9,所以 , , 的实部依次成等比数列,故B正确;
因为 , , 的虚部分别为 , ,1,所以 , , 的虚部依次不成等差数列,故D错误;
,故C正确.
故选:ABC.
10.已知 为坐标原点,点 为抛物线 : 的焦点,点 ,直线 : 交抛物
线 于 , 两点(不与 点重合),则以下说法正确的是( )
A.
B. 存在实数 ,使得
C. 若 ,则
D. 若直线 与 的倾斜角互补,则
【答案】ACD
【解析】由已知,抛物线 : ,∴ , ,焦点 ,
不妨设为 , ,设 , 到准线的距离分别为 , ,
对于A,∵由标准方程知,抛物线顶点在原点,开口向右, ,
∴由抛物线的定义 ,故选项A正确;
对于B, 消去 ,化简得 ( ),
则 , ,∵ ,∴ ,∴ ,
∵ , ,∴ ,
∴ ,∴ ,
∴不存在实数 ,使得 ,选项B错误;
对于C, , ,
∵ ,∴ ,∴
又∵由选项B判断过程知 , ,
∴解得 , , 或 , , ,
∴若 ,则 ,选项C正确;对于D,由题意, , , , ,
直线 与 的倾斜角互补时,斜率均存在,且 ,
∴ ,代入 , ,化简得 ,
由选项B的判断知, ,
∴ ,∴ ,故选项D正确.
故选:ACD.
11.已知函数 定义域为R,满足 ,当 时, .若函数
的图象与函数 的图象的交点为 , ,
,(其中 表示不超过 的最大整数),则( )
A. 是偶函数 B.
B. C. D.
【答案】BC
【解析】函数 ,显然 ,而 ,即 ,
因此 不是偶函数,A错误;
函数 定义域为 ,满足 ,当 时, ,
当 时, , ,
当 时, ,
,
当 时, , ,
当 时, ,
,
因此当 时,函数 在 上递减,
在 上递增,当 时, 取得最大值 ,
当 时, , ,
当 时, , ,当 时, , ,
因此当 时,函数 ,
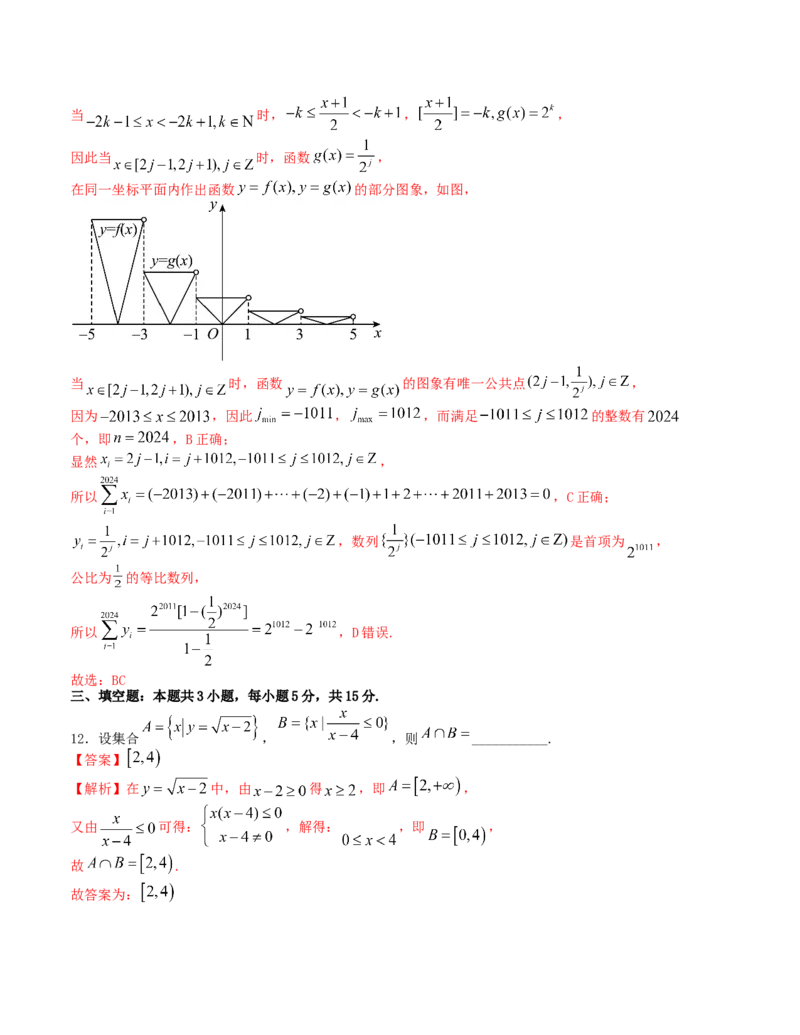
在同一坐标平面内作出函数 的部分图象,如图,
当 时,函数 的图象有唯一公共点 ,
因为 ,因此 , ,而满足 的整数有
个,即 ,B正确;
显然 ,
所以 ,C正确;
,数列 是首项为 ,
公比为 的等比数列,
所以 ,D错误.
故选:BC
三、填空题:本题共3小题,每小题5分,共15分.
12.设集合 , ,则 ___________.
【答案】
【解析】在 中,由 得 ,即 ,
又由 可得: ,解得: ,即 ,
故 .
故答案为:13.函数 ,若 ,则 的最小值为___________.
【答案】
【解析】因为 的定义域为 ,
,所以 在 为增函数,
,所以 ,
又 , 在 为增函数,所以 ,即 ,
因为 , ,当且仅当 ,即 时,等
号成立,
所以 的最小值为 .
故答案为:
14.已知反比例函数图象上三点 的坐标分别 , 与 ,
过B作直线 的垂线,垂足为Q.若 恒成立,则a的取值范围为___________.
【答案】
【解析】由题意得:反比例函数为 ,因为点P在反比例函数图象上,所以 ,
,所以
,
记 ,由题意得: 恒成立,
当 ,则 ,解得: ,由于 ,故 ;
下面证明当 时, 恒成立,即因为 是开口向上的二次函数,
所以
;
② ,
令 ,则 ,开口向下,对称轴为 ,故
在 上单调递减,故 .
所以当 时, 恒成立,故a的取值范围是
故答案为: