文档内容
石河子第一中学 2025届高三年级开学考试 数学试卷
一、单项选择题:(本大题8小题,每小题5分,共40分.在每小题给出的四个选项中,只
有一项是符合题目要求的.)
1.已知集合 , ,则 ( )
A. B. C. D.
2.下列不等式中,可以作为 的一个必要不充分条件的是( )
A. B. C. D.
3.若 ,且 ,则下列不等式中一定成立的是( )
A. B. C. D.
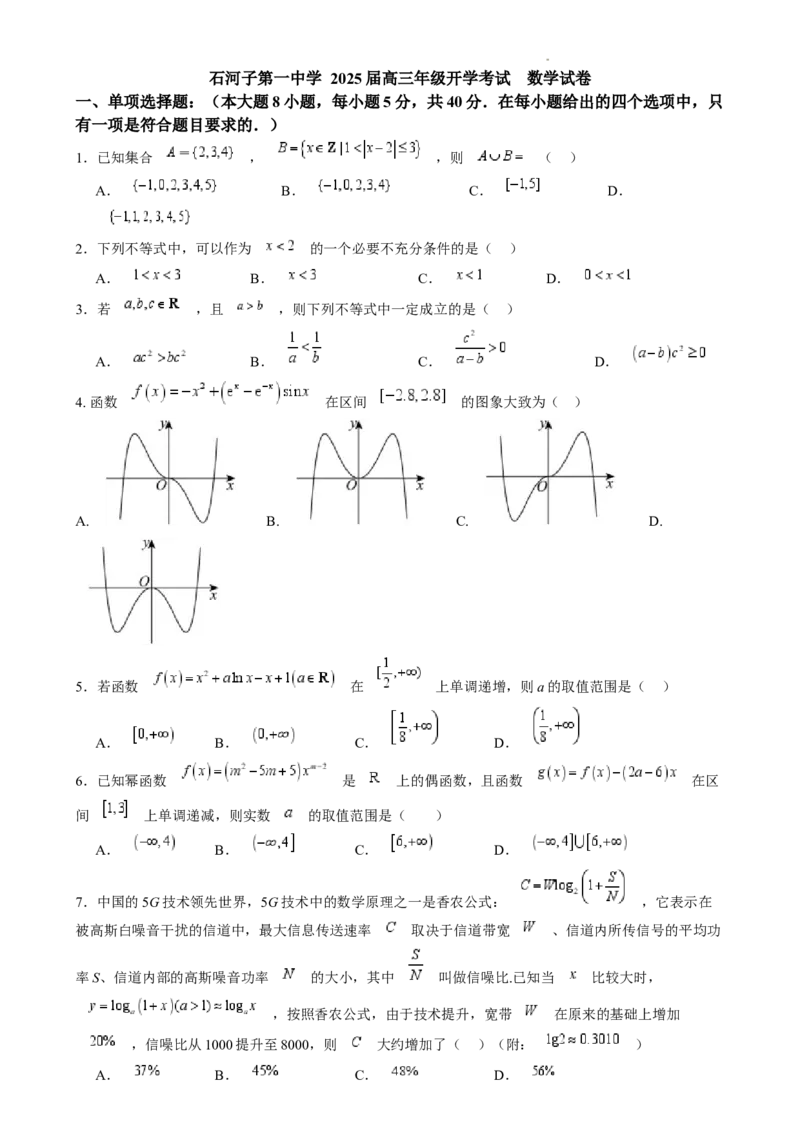
4. 函数 在区间 的图象大致为( )
A. B. C. D.
5.若函数 在 上单调递增,则a的取值范围是( )
A. B. C. D.
6.已知幂函数 是 上的偶函数,且函数 在区
间 上单调递减,则实数 的取值范围是( )
A. B. C. D.
7.中国的5G技术领先世界,5G技术中的数学原理之一是香农公式: ,它表示在
被高斯白噪音干扰的信道中,最大信息传送速率 取决于信道带宽 、信道内所传信号的平均功
率S、信道内部的高斯噪音功率 的大小,其中 叫做信噪比.已知当 比较大时,
,按照香农公式,由于技术提升,宽带 在原来的基础上增加
,信噪比从1000提升至8000,则 大约增加了( )(附: )
A. B. C. D.8. 已知函数 的定义域为R, ,且当 时 ,则
下列结论中一定正确的是( )A. B. C.
D.
二、选择题:本题共 3 小题,每小题 6 分,共 18 分. 在每小题给出的选项中,有多项符合题
目要求.
全部选对得 6 分,部分选对的得部分分,选对但不全的得部分分,有选错的得0分.
9.已知奇函数 的定义域为 ,若 ,则( )
A. B. 的图象关于直线 对称
C. D. 的一个周期为
10. 设函数 ,则( )
A. 当 时, 有三个零点 B. 当 时, 是
的极大值点
C. 存在a,b,使得 为曲线 的对称轴 D. 存在a,使得点 为曲线
的对称中心
11.已知 , 则下列结论正确的有( )
A. 的最大值为 B. 的最小值为 C. 的最
小值为3 D.
三、填空题:本题共 3 小题,每小题 5 分,共 15 分.
12.函数 有零点,但不能用二分法求出,则a,b的关系是 ,函数的零点是
(用a表示).
13. 若曲线 在点 处的切线也是曲线 的切线,则
__________.
14.已知 为实数,若不等式 对任意 恒成立,
则 的最大值是 .
四、解答题:本题共5小题,共77分.解答应写出文字说明、证明过程或演算步骤.
15.(13分)已知不等式 的解集为 .
(1)求 的值, (2)若 , , ,求 的最小值.16(15分).已知函数 .
(1)作出函数 的大致图像,并简要说明理由;
(2)讨论函数 的单调性.
17. ( 15 分 ) 设 函 数 , 直 线 是 曲 线 在 点
处的切线.
(1)当 时,求 在点 处的切线方程.
(2)求证: 不经过点 .
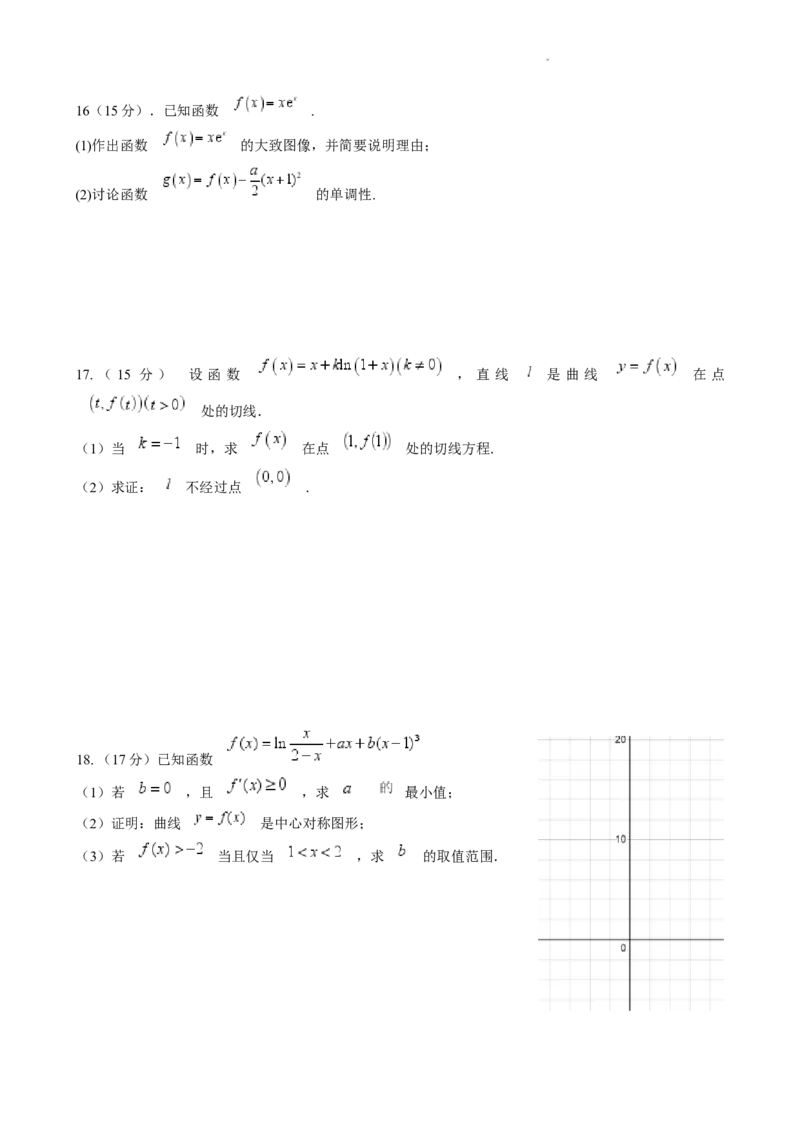
18. (17分)已知函数
(1)若 ,且 ,求 最小值;
(2)证明:曲线 是中心对称图形;
(3)若 当且仅当 ,求 的取值范围.19.(17分)给定整数 ,由 元实数集合 定义其随影数集 .
若 ,则称集合 为一个 元理想数集,并定义 的理数 为其中所有元素的
绝对值之和.
(1)分别判断集合 是不是理想数集;(结论不要求说明理由)
(2)任取一个5元理想数集 ,求证: ;
注:①由 个实数组成的集合叫做 元实数集合, 分别表示数集 中的
最大数与最小数.
②已知 ,例如 。