文档内容
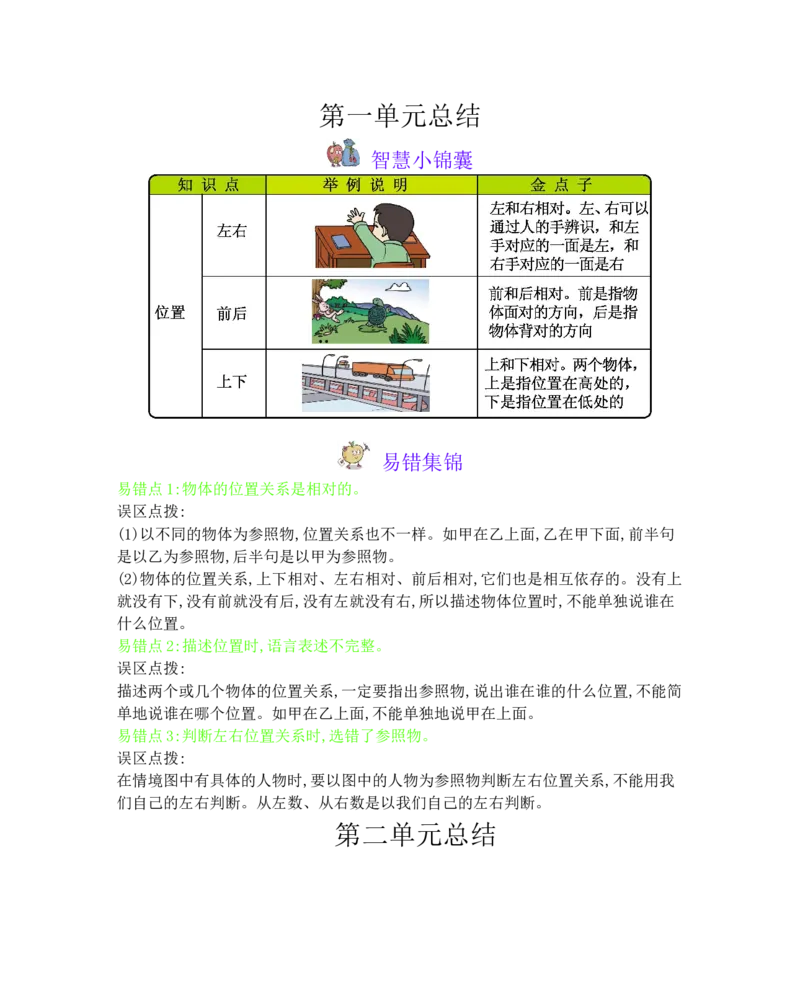
第一单元总结
智慧小锦囊
易错集锦
易错点1:物体的位置关系是相对的。
误区点拨:
(1)以不同的物体为参照物,位置关系也不一样。如甲在乙上面,乙在甲下面,前半句
是以乙为参照物,后半句是以甲为参照物。
(2)物体的位置关系,上下相对、左右相对、前后相对,它们也是相互依存的。没有上
就没有下,没有前就没有后,没有左就没有右,所以描述物体位置时,不能单独说谁在
什么位置。
易错点2:描述位置时,语言表述不完整。
误区点拨:
描述两个或几个物体的位置关系,一定要指出参照物,说出谁在谁的什么位置,不能简
单地说谁在哪个位置。如甲在乙上面,不能单独地说甲在上面。
易错点3:判断左右位置关系时,选错了参照物。
误区点拨:
在情境图中有具体的人物时,要以图中的人物为参照物判断左右位置关系,不能用我
们自己的左右判断。从左数、从右数是以我们自己的左右判断。
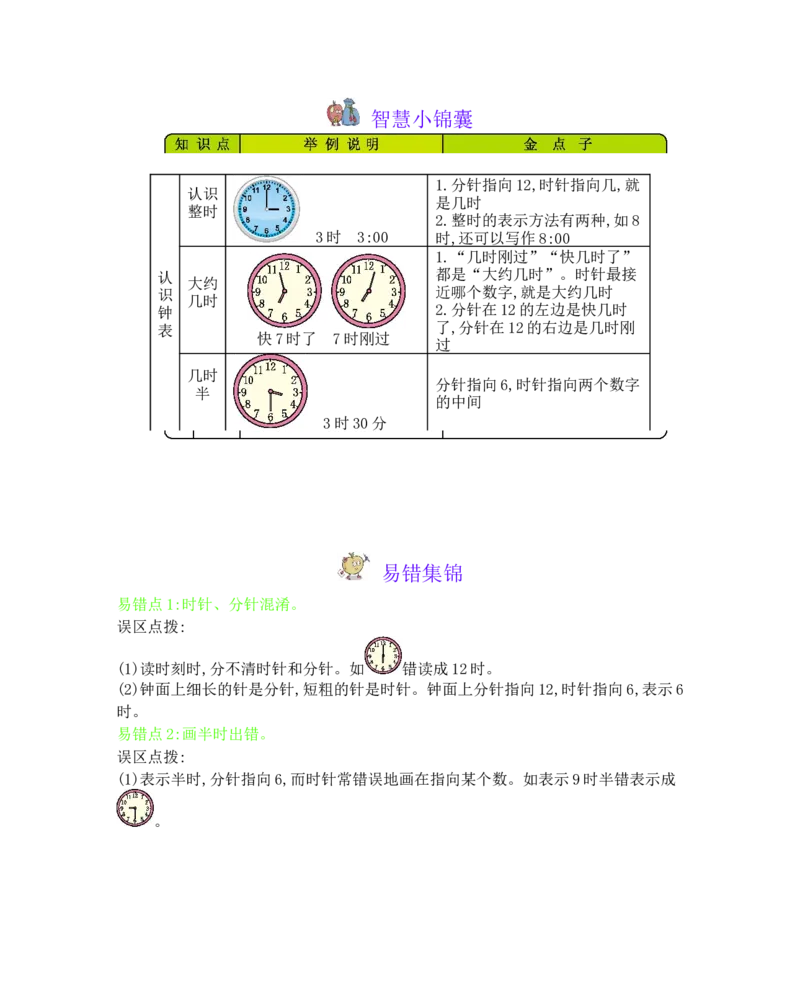
第二单元总结智慧小锦囊
1.分针指向12,时针指向几,就
认识
是几时
整时
2.整时的表示方法有两种,如8
3时 3:00 时,还可以写作8:00
1.“几时刚过”“快几时了”
认 都是“大约几时”。时针最接
大约
识 近哪个数字,就是大约几时
几时
钟 2.分针在12的左边是快几时
表 了,分针在12的右边是几时刚
快7时了 7时刚过
过
几时
分针指向6,时针指向两个数字
半
的中间
3时30分
易错集锦
易错点1:时针、分针混淆。
误区点拨:
(1)读时刻时,分不清时针和分针。如 错读成12时。
(2)钟面上细长的针是分针,短粗的针是时针。钟面上分针指向12,时针指向6,表示6
时。
易错点2:画半时出错。
误区点拨:
(1)表示半时,分针指向6,而时针常错误地画在指向某个数。如表示9时半错表示成
。(2)半时的分针指向6,但时针并不是正好指向某个数字,应该指在两个数字的中间,9
时半的时针在9和10中间,正确的表示方法为 。
第三单元总结
智慧小锦囊
在括号里填上合适的 数数的方法:一个一个地数,两个
数。 两个地数,五个五个地数,十个十
数数
1.36,37,38,(39),(40) 个地数……几十九后面一个数是
2.50,55,60,(65),(70) 几加1个十
数的 3个十和8个一合起来是 几个十和几个一合起来是几十几;
组成 38 几十几里面有几个十和几个一
数位顺序表
…百十个
…位位位
读数时,从高位读起,十位上是几
数的 36读作:三十六 就读几十,个位上是几就读几,整
以
读写 八十四写作:84 十数末尾的“0”不读。写数时,
内
也从高位写起,几十就在十位上写
数
几,几个就在个位上写几,如果个
的
位上一个计数单位也没有,就用0
认
占位
识
数的大小比较:先比较位数,位数
比较 多的数一定大于位数少的数。位
100>99 59<60
数的 数相同看高位,高位相同依次往下
47>46
大小 看,相同数位上的数字大的这个数
就大
描述 1.用“多一些”“多得多”“少
两个 17比20少一些,100比 一些”“少得多”描述数量关系,
数的 20多得多,98比90多一 是根据两个数相差多少的程度不
大小 些,10比80少得多 同决定的
关系 2.两个数相差较多用“多(少)得多”描述,两个数相差不多时,用
“多(少)一些”描述
易错集锦
易错点1:数数出错。
误区点拨:
(1)几十九后面该数多少,常会出现错误。没有弄清整十数的顺序是出错的原因之一。
(2)几十九是由几个十和9个一组成的,再添上1,和9又组成1个十,和前面的几个十
组成下一个整十数。如79后面是80,89后面是90。
易错点2:读数出错。
误区点拨:
(1)读两位数时依次读出每个数字。如“58”错读成“五八”。
(2)读两位数时,应该从十位读起,十位上的数字是几就读几十;再读个位上的数字,个
位上的数字是几就读几。如“58”读作“五十八”。
易错点3:写出计数器表示的数出错。
误区点拨:
(1)个位上没有珠子时,写数时忘记写0(如右图)。
(2)写计数器表示的数,十位上有几个珠子就在十位上写几,个位上有几个珠子就在个
位上写几。如果个位上一个珠子也没有,就在个位上写0。
易错点4:比较数的大小时出错。
误区点拨:
(1)位数不同的数,错误地认为应该直接从高位比起。如比较100和99,认为1<9,就
误认为100<99。
(2)在比较数的大小时,先比较位数,位数多的数大;位数相同的再从高位比起,相同数
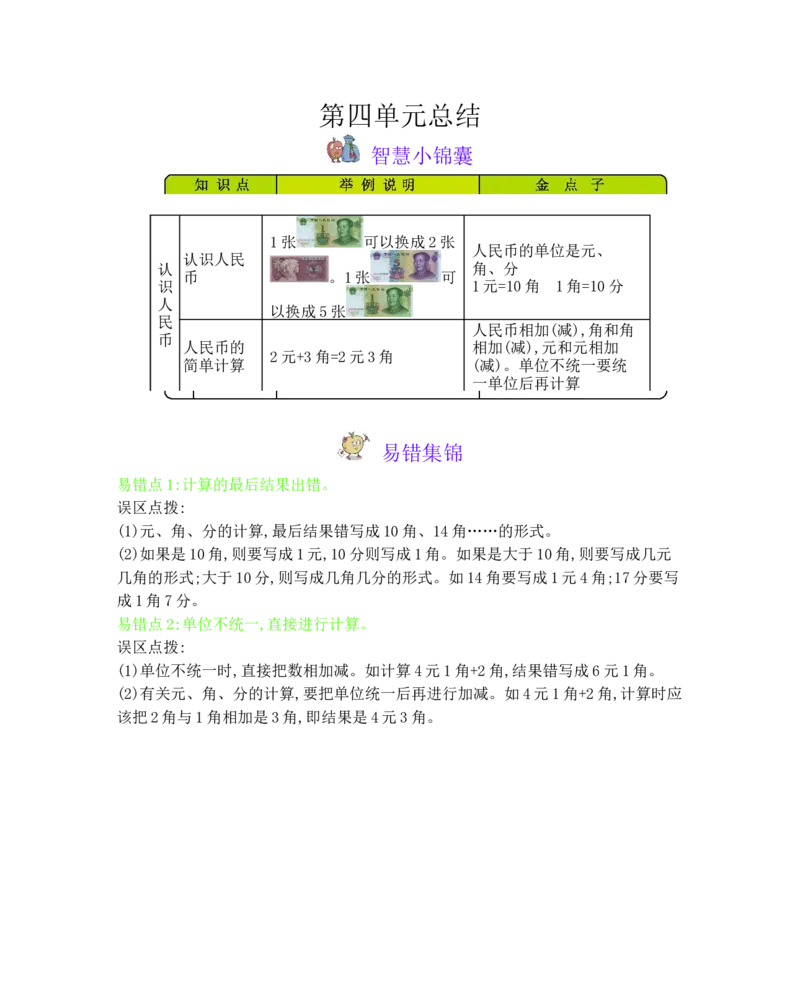
位上的数字大的那个数大。第四单元总结
智慧小锦囊
1张 可以换成2张
人民币的单位是元、
认识人民
认 角、分
币 。1张 可
识 1元=10角 1角=10分
人
以换成5张
民
人民币相加(减),角和角
币
人民币的 相加(减),元和元相加
2元+3角=2元3角
简单计算 (减)。单位不统一要统
一单位后再计算
易错集锦
易错点1:计算的最后结果出错。
误区点拨:
(1)元、角、分的计算,最后结果错写成10角、14角……的形式。
(2)如果是10角,则要写成1元,10分则写成1角。如果是大于10角,则要写成几元
几角的形式;大于10分,则写成几角几分的形式。如14角要写成1元4角;17分要写
成1角7分。
易错点2:单位不统一,直接进行计算。
误区点拨:
(1)单位不统一时,直接把数相加减。如计算4元1角+2角,结果错写成6元1角。
(2)有关元、角、分的计算,要把单位统一后再进行加减。如4元1角+2角,计算时应
该把2角与1角相加是3角,即结果是4元3角。第五单元总结
智慧小锦囊
1.整十数加一位数:想几个十
整十
40+5=45中,40和5都是加 和几个一合起来是几十几。相
数加
数,45是和 应的减法:从几十几里面减去
减一
37-7=30中,37是被减数,7 几个一剩几个十
位数
是减数,30是差 2.加数+加数=和
以
被减数-减数=差
内
两位
的 两位数加、减整十数:先把两
数加 20+16=36
加 位数分成整十数和一位数,然
减整 先算20+10=30,再算
法 后把整十数相加或相减,最后
十数 30+6=36
和 加上一位数
减
两位 32+8=40
法
数加 32 两位数加一位数的竖式计算:
(
一位 + 8 相同数位对齐,从个位加起,个
一 1
数 40 位相加满十,向十位进1
)
两位 两位数减一位数的竖式计算:
56-8=48
数减 · 相同数位对齐,从个位减起,个
6
5
一位 位不够减,向十位借1再减,同- 8
数
48 时十位上的数必须减1
求比
一个
数多
已知两个数,求一个数比另一
多少 爷爷今年65岁,小明今年6
个数多多少或少多少,用减法
或少 岁,求爷爷比小明大多少岁,
计算,用较大数减较小数就等
多少 列式为65-6=59(岁)
于它们相差的数
的问
题
易错集锦
易错点1:计算两位数加、减一位数容易出现对位错误。
误区点拨:
(1)计算两位数加、减一位数,一位数会和十位数进行加减。
(2)计算两位数加、减一位数,要从低位开始计算,相同数位上的数才能相加减。
易错点2:两位数加、减一位数计算错误。
误区点拨:
(1)计算两位数加、减一位数,计算十位时,没有计算十位上的进位数或退位数。
(2)竖式计算加减法时,相同数位对齐,从个位算起。计算加法,个位满十向十位进1,
十位数字相加时,不要忘记加进位数1。 计算减法,个位不够减,从十位退一当十,和
个位数字合起来继续减,同时十位上的数减1。为了防止出错,计算时在相应位置点
退位点或写进位数。
易错点3:弄不清大数、小数、相差数之间的关系。
误区点拨:
(1)首先应弄清所要求的数是大数、小数还是相差数,再根据三者之间的关系正确计
算。
(2)求两数相差多少用减法计算,求它们的和用加法计算。第六单元总结
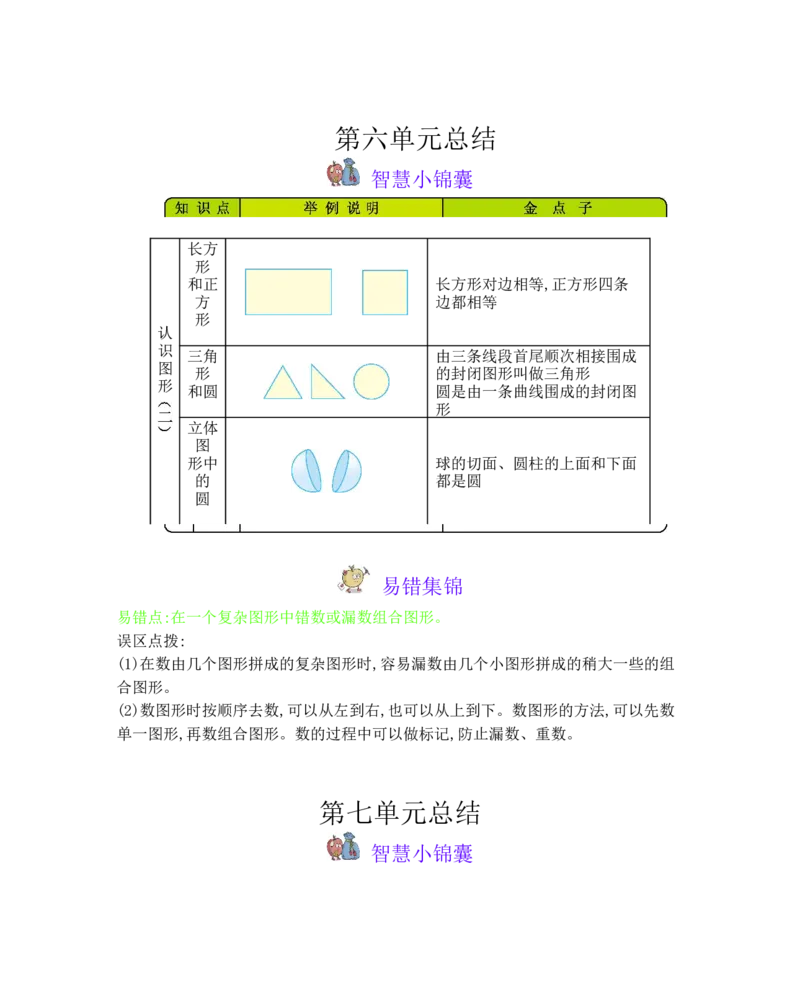
智慧小锦囊
长方
形
和正 长方形对边相等,正方形四条
方 边都相等
形
认
识
三角 由三条线段首尾顺次相接围成
图
形 的封闭图形叫做三角形
形
和圆 圆是由一条曲线围成的封闭图
形
立体
图
形中 球的切面、圆柱的上面和下面
的 都是圆
圆
易错集锦
易错点:在一个复杂图形中错数或漏数组合图形。
误区点拨:
(1)在数由几个图形拼成的复杂图形时,容易漏数由几个小图形拼成的稍大一些的组
合图形。
(2)数图形时按顺序去数,可以从左到右,也可以从上到下。数图形的方法,可以先数
单一图形,再数组合图形。数的过程中可以做标记,防止漏数、重数。
第七单元总结
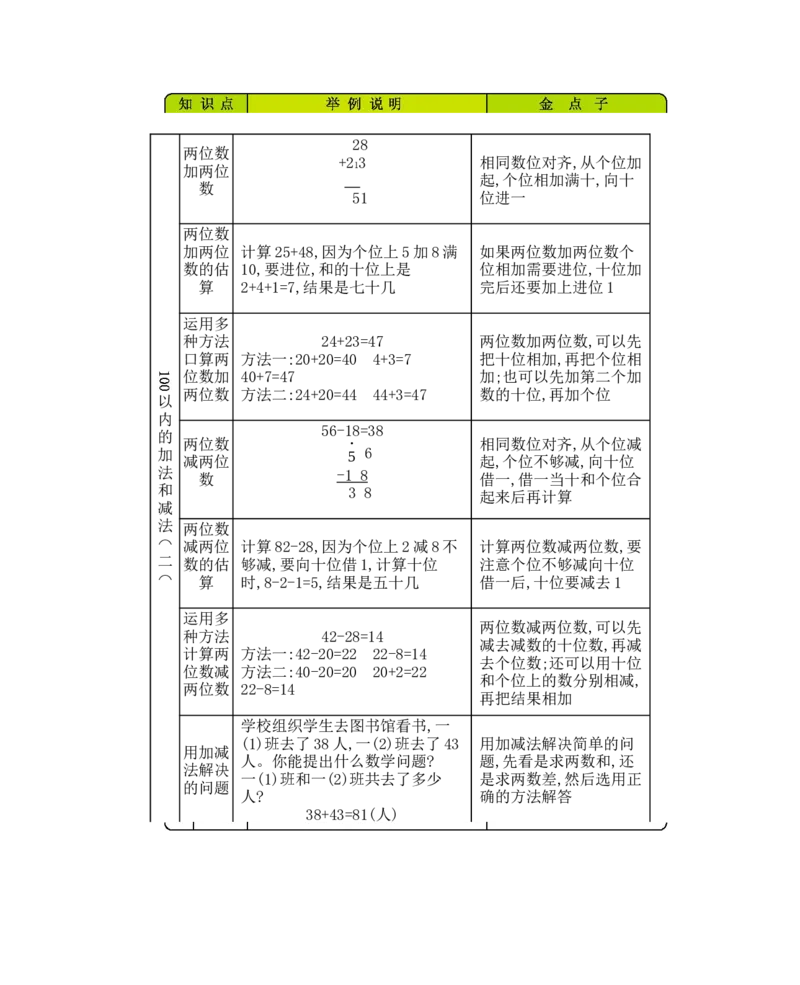
智慧小锦囊28
两位数
+2 3 相同数位对齐,从个位加
加两位 1
起,个位相加满十,向十
数
51 位进一
两位数
加两位 计算25+48,因为个位上5加8满 如果两位数加两位数个
数的估 10,要进位,和的十位上是 位相加需要进位,十位加
算 2+4+1=7,结果是七十几 完后还要加上进位1
运用多
种方法 24+23=47 两位数加两位数,可以先
口算两 方法一:20+20=40 4+3=7 把十位相加,再把个位相
位数加 40+7=47 加;也可以先加第二个加
两位数 方法二:24+20=44 44+3=47 数的十位,再加个位
以
内
56-18=38
的
两位数 · 相同数位对齐,从个位减
加 5 6
减两位 起,个位不够减,向十位
法 - 1 8
数 借一,借一当十和个位合
和 3 8
起来后再计算
减
法 两位数
⌒ 减两位 计算82-28,因为个位上2减8不 计算两位数减两位数,要
二 数的估 够减,要向十位借1,计算十位 注意个位不够减向十位
⌒ 算 时,8-2-1=5,结果是五十几 借一后,十位要减去1
运用多
两位数减两位数,可以先
种方法 42-28=14
减去减数的十位数,再减
计算两 方法一:42-20=22 22-8=14
去个位数;还可以用十位
位数减 方法二:40-20=20 20+2=22
和个位上的数分别相减,
两位数 22-8=14
再把结果相加
学校组织学生去图书馆看书,一
(1)班去了38人,一(2)班去了43 用加减法解决简单的问
用加减
人。你能提出什么数学问题? 题,先看是求两数和,还
法解决
一(1)班和一(2)班共去了多少 是求两数差,然后选用正
的问题
人? 确的方法解答
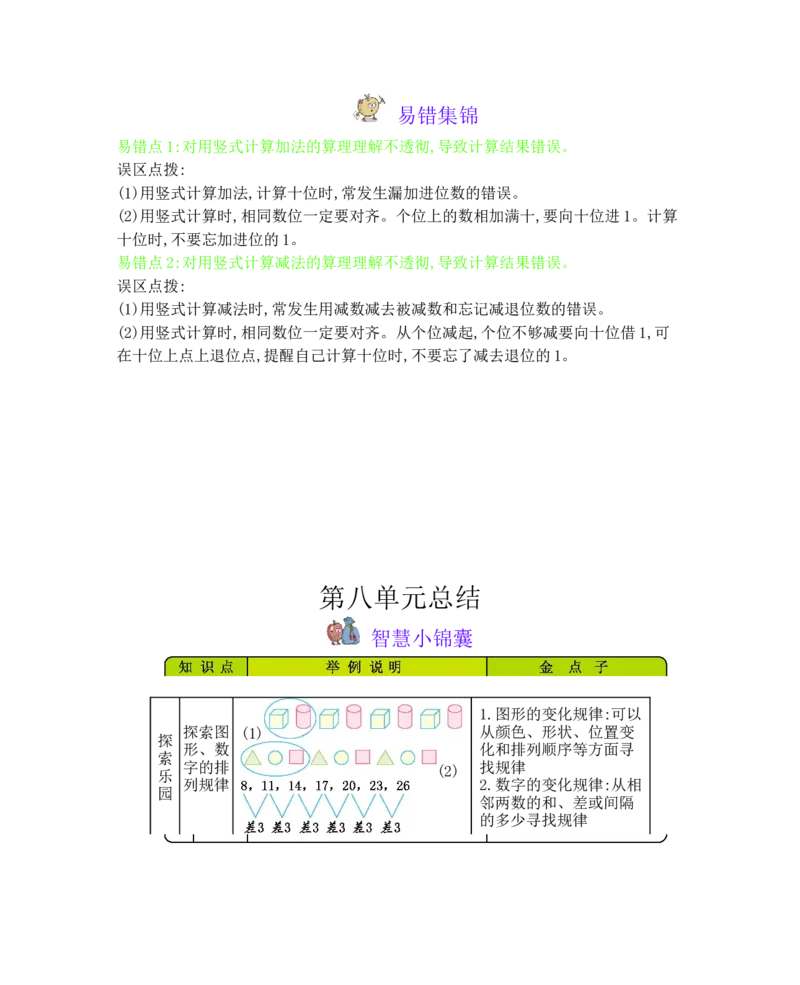
38+43=81(人)易错集锦
易错点1:对用竖式计算加法的算理理解不透彻,导致计算结果错误。
误区点拨:
(1)用竖式计算加法,计算十位时,常发生漏加进位数的错误。
(2)用竖式计算时,相同数位一定要对齐。个位上的数相加满十,要向十位进1。计算
十位时,不要忘加进位的1。
易错点2:对用竖式计算减法的算理理解不透彻,导致计算结果错误。
误区点拨:
(1)用竖式计算减法时,常发生用减数减去被减数和忘记减退位数的错误。
(2)用竖式计算时,相同数位一定要对齐。从个位减起,个位不够减要向十位借1,可
在十位上点上退位点,提醒自己计算十位时,不要忘了减去退位的1。
第八单元总结
智慧小锦囊
1.图形的变化规律:可以
探索图 (1) 从颜色、形状、位置变
探
形、数 化和排列顺序等方面寻
索
字的排 (2) 找规律
乐
列规律 2.数字的变化规律:从相
园
邻两数的和、差或间隔
的多少寻找规律易错集锦
易错点1:对“规律”理解不清。
误区点拨:
(1)一组物体循环出现两次以上才能成为规律,否则不能成为规律,如1、1、2。
(2)判断物体的排列规律,从颜色、形状、大小、多少等特征去判断。如果物体出现
的次数较少,判断出来的规律可能有多种,所以要判断出唯一的、正确的规律一定要
有3组或更多组排列。如1、1、2、4、7……这是在前一个数的基础上依次加0、
1、2、3……如果是1、1、2就不能找到规律。
易错点2:数字排列不能只看两个数之间相差几,还要看间隔的数。
误区点拨:
数字排列找规律时一定要仔细,不能仅限于一种加法或是减法,要多角度地思考排列
规律。如19,8,17,8,15,8,13,8把每两个数中间的8忽略就很容易地找到规律。