2024年新高考联考协作体高三2月收心考试-数学试题答案(1)_2024年4月_01按日期_6号_2024届新结构高考数学合集_新高考19题（九省联考模式）数学合集140套

2024 年新高考联考协作体高三 2 月收心考试
高三数学参考答案
一、选择题
题号 1 2 3 4 5 6 7 8 9 10 11
答案 B D A C B D B C ACD AC ABD
【解析】
4、【解析】假设经过n年后年全年投入的研发资金开始超过200万元，即160(1.1)n 200
13lg2 0.1
所以n  2.5，因此超过200万元的年份是2026年.答案选C.
lg1.1 0.04

 
   (a2e)e      
5、【解析】a2e在e 上的投影向量为  e (ae 2)e，所以ae 3，
e
   
  2
因为|2ea| 1044ea a 10 a 3 2
  2 
所以：a与e夹角的余弦值为 ，所以夹角为 .答案选B.
2 4
2x 8x 2x 8x 2x 8x 2x 8x 8x 2x
6、【解析】因为 f(x) (a 0且a 1)是偶函数，所以  , ax
xax xax (x)ax ax 2x8x
因此：a2x 2x8xa2 16,a 4(舍负)，因此答案选D.
1
7、【解析】设APC ,S  |PA|2 sin2
PAB
2
1 1 1 3 1 tan 3
直角三角形APC，PA ，所以 sin2   
tan 2 tan2 12 tan2 1tan2 12

整理可得：tan3tan4 3 0tan 3,
3
1 2 3
因此PC   ，答案选B(本题带选项验算也可以).
sin 3
8、【解析】取两种特殊情况说明：k 1时显然成立；当k 4时，理由如下
因为a 是等比数列，设公比为qq0，则a 0，
n n
当tN，a a 时，a aq4，即a  q2 1  q2 1  0，
t t4 t t t
若a 0，则1q1
t
*数学答案(共 9 页)第 1 页
{#{QQABaQSEggiIAAJAAQgCAw16CAAQkAACAKoOxAAAsAABCQFABAA=}#}注意到，当q0时，a aq0，与假设矛盾，舍去，
t1 t
故0 q1，此时a a qa ，则a 为递减数列；
t1 t t n
若a 0，则q1或q 1，，
t
注意到，当q1时，a aq0，与假设矛盾，舍去，
t1 t
故q1，此时a a qa ，则a 为递减数列；
t1 t t n
综上：当tN，a a 时，a 为递减数列，即充分性成立；
t t4 n
当a 为递减数列时，a a a  a  a ，即tN，a a 成立，即必要性成立；
n t t1 t2 t3 t4 t t4
故选：C.
9、【解析】设弧 AD 所在圆的半径为 R，弧 BC 所在圆的半径为 r，弧 AD 的长度是弧 BC 长度的 3 倍，
  3
 R 3 r,即R 3r,CD  Rr 2r 2,r 1,R 3 ，所以弧 AD 的长度为  ；曲池的体积为
2 2 2
1 1
V ( R2 r2)AA 10；
4 4 1
1 1 1 1
曲池的表面积为( R2 r2)2( R r)52522014；
4 4 2 2
1
三棱锥ACC D的体积为 355.答案选：ACD.
1 3
3
10、【解析】当 a 1时， y |x3 3ax|在区间( ,2)上单调递减，因为函数 y |x33ax|在x 0上的单调递减
2
a 1

 3 4 9
区间为( a, 3a)，所以 a  ，因此 a  ；
2 3 4

  3a 2
3
当 0 a 1时， y |x3 3ax|在区间( ,2)上单调递增，因为函数 y |x33ax|在x 0上的单调递增区间为
2
0a 1
 3
(0, a),( 3a,)，所以 3因此0a 
3a  4

 2
答案选AC.
11、【解析】因为(a a )2 3(a a )2,a 1，所以a a 1或a a  2，因此A，B是正确的.相邻
n1 n n1 n 1 n1 n n1 n
两项的差值最小为1，最大为2，所以当{a }是以1为首项，以1为公差时，S 取最小值为66；当{a }是以1为首项，
n 11 n
*数学答案(共 9 页)第 2 页
{#{QQABaQSEggiIAAJAAQgCAw16CAAQkAACAKoOxAAAsAABCQFABAA=}#}以2为公差时，S 取最大值为121；且S 取值一定是正整数，所以S 的取值个数为121-66+1=56,所以C不对.
11 11 11
2a  a a a a  a a (a a )(a a )(a a )(a a )，
6 1 11 6 1 11 6 6 5 2 1 11 10 7 6
所以满足2a  a a 的数列{a }的个数为
6 1 11 n
C0C0 C1C1C2C2 C3C3 C4C4 C5C5  252.答案ABD.
5 5 5 5 5 5 5 5 5 5 5 5
二、非选择题
325  2 5
12. ③ 13.  14. [ , ][ ,]
9 2 3 6
【解析】
13、【解析】
连接AC ，即求三角形ACD的外接圆的面积.
3
直角三角形ABC中，AB6,BC 8,AC 10，所以sinACB
5
3
ADBC,sinDAC  ，
5
直角梯形ABCD中，DC 2 13，
2 13 10 13
三角形ACD的外接圆直径为：2R   ，
3 3
5
325
因此三角形ACD的外接圆的面积 
9
14、【解析】
 
由已知可知g(x)4sin(2x)3，因为对任意x [0, ]，都存在x [ ，0]，使得 f(x )  g(x )，所以
1 2 2 4 1 2
 
f(x)在x[0, ]上的值域是g(x)在x[ ，0]上值域的子集
2 4
  
f(x)在x[0, ]上的值域[-1,1]，且x[ ，0],2x[ ,]
2 4 2
  
因为g(x)值域中一定有1这个元素，所以 2k[ ,],kZ[ ,]（必要条件）
2 2 2

还需要约束g(x)的最小值小于等于-1，所以4sin( )31或者4sin31
2
1 1  2 5
因此sin 或者cos ，所以[ , ][ ,].
2 2 2 3 6
 cosB 3 
15.（1）当C  时，  ，所以2cos(B )1,B(0,)
6 1sinB 3 6
*数学答案(共 9 页)第 3 页
{#{QQABaQSEggiIAAJAAQgCAw16CAAQkAACAKoOxAAAsAABCQFABAA=}#}
因此B ；……………………………………………………5分
6
cosB
（2）  tanC,cosBcosCsinBsinC sinC
1sinB

化简得cos(BC)sinCsin(A )sinC ………………………8分
2
  
因此：AC ,B  2C(0C  )
2 2 4
7 7 7 7
b c则sinB  sinC,cos2C  sinC,2sin2C sinC10………………………11分
2 2 2 2
1
所以sinC  或sinC  2(舍)
4
1
因此sinC  .………………………13分
4
16.（1）摸球两次停止摸球说明前面两次摸到的是白色球，记事件A,i 1,2为“第i次摸球的颜色是白色”
i
2 1 1
因此P(A A )   ；………………………………………………4分
1 2 6 5 15
（2）X 的可能取值为2，3，4，5
2 1 1
P(X  2)  
6 5 15
2 4 1 2
P(X 3) 2   
6 5 4 15 ………………………7分
4 3 2 1 2 4 3 1 4
P(X  4)    3    
6 5 4 3 6 5 4 3 15………………………10分
8
P(X 5)1P(X  2)P(X 3)P(X  4)
15………………………13分
X 2 3 4 5
1 2 4 8
P
15 15 15 15
261640 64
E(X) 
15 15
64
因此X 的期望为 .………………………………………………15分
15
17.因为PA底面ABCD，四边形ABCD为菱形，取CD中点H，
AB  AD 2,BD 2 3,BAD 120 。，ACD是等边三角形，AH CD
*数学答案(共 9 页)第 4 页
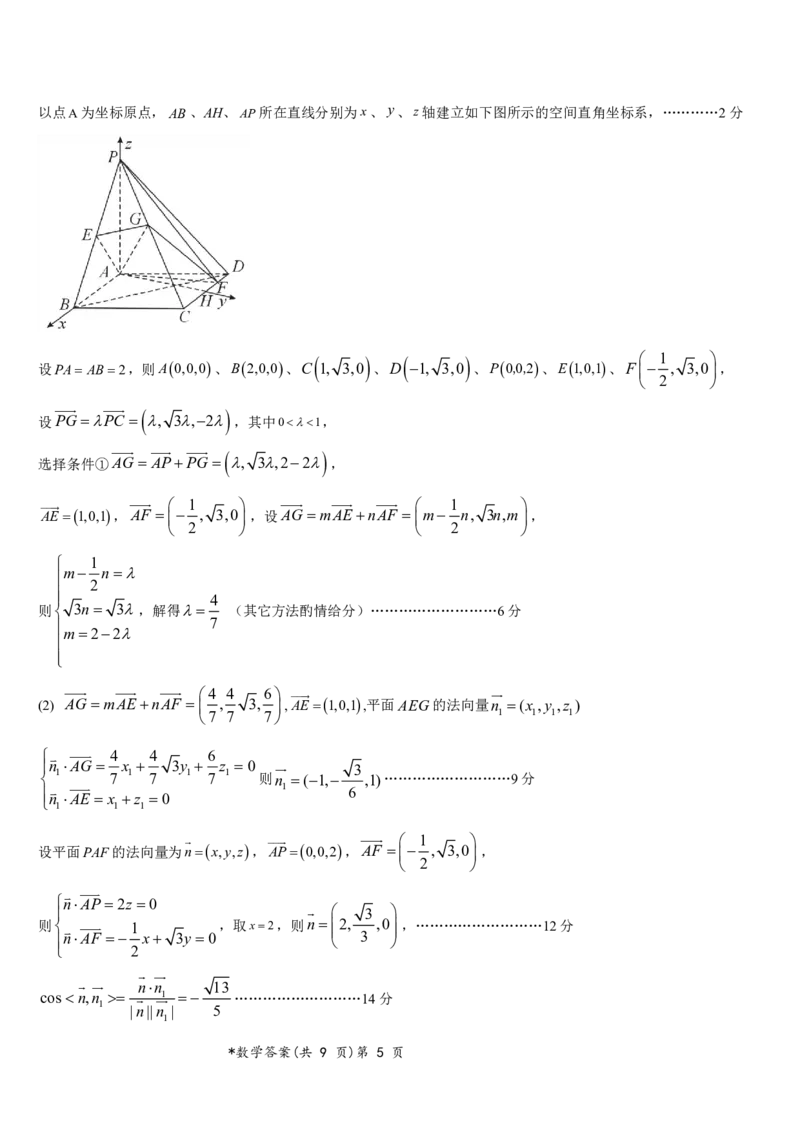
{#{QQABaQSEggiIAAJAAQgCAw16CAAQkAACAKoOxAAAsAABCQFABAA=}#}以点A为坐标原点，AB、AH、AP所在直线分别为x、y、z轴建立如下图所示的空间直角坐标系，…………2分
     1 
设PA AB2，则A0,0,0、B2,0,0、C 1, 3,0 、D 1, 3,0 、P0,0,2、E1,0,1、F  , 3,0，
 2 
 
 
设PG PC  , 3,2 ，其中01，
  
 
选择条件①AG  APPG  , 3,22 ，
uuur   1      1 
AE1,0,1，AF    , 3,0 ，设AG mAEnAF  m n, 3n,m，
 2   2 
 1
m n

2

 4
则 3n 3，解得 （其它方法酌情给分）………………………6分
 7
m22


   4 4 6 uuur 
(2) AG mAEnAF   , 3, ,AE1,0,1 ,平面AEG的法向量n (x ,y ,z )
7 7 7 1 1 1 1
  4 4 6
n AG  x  3y  z  0  3
 1 7 1 7 1 7 1 则n (1, ,1)………………………9分
 n    A  E   x z  0 1 6
1 1 1
    1 
设平面PAF的法向量为nx,y,z，AP0,0,2，AF    , 3,0 ，
 2 


nAP  2z 0
   3 
则   1 ，取x2，则n  2, ,0  ，………………………12分
nAF  x 3y  0  3 
 2
 
  nn 13
cosn,n   1  ………………………14分
1 |n||n | 5
1
*数学答案(共 9 页)第 5 页
{#{QQABaQSEggiIAAJAAQgCAw16CAAQkAACAKoOxAAAsAABCQFABAA=}#}13
平面AEG与平面APF 所成二面角的余弦值为 ………………………15分
5
   
选择条件②AG  , 3,22 ，BP2,0,2，
    2
若AG平面PBD，因为AGBD 0且AGBP2440，解得 ， ………………………6分
3
 2 2 3 2 uuur 
（2）AG ( , , ),AE1,0,1 ,平面AEG的法向量n (x ,y ,z )
1 1 1 1
3 3 3
   2 2 3 2
n AG  x  y  z  0 
 1 3 1 3 1 3 1 则n (1,0,1)………………………9分
 1

n AE  x z  0
1 1 1
    1 
设平面PAF的法向量为nx,y,z，AP0,0,2，AF    , 3,0 ，
 2 


nAP  2z 0
   3 
则   1 ，取x2，则n  2, ,0  ，………………………12分
nAF  x 3y  0  3 
 2
 
  nn 78
cosn,n   1  ………………………14分
1 |n||n | 13
1
78
平面AEG与平面APF 所成角的余弦值为 .………………………15分
13
    1 
选择条件③设平面PAF的法向量为nx,y,z，AP0,0,2，AF    , 3,0 ，
 2 


nAP  2z 0
   3 
则   1 ，取x2，则n  2, ,0  ，
nAF  x 3y  0  3 
 2
  
   
EG EPPG 1,0,1  , 3,2  1, 3,12 ，
  2
若EG//平面PAF，则EGn22320，解得 ，………………………6分
3
 2 2 3 2 uuur 
（2）AG ( , , ),AE1,0,1 ,平面AEG的法向量n (x ,y ,z )
1 1 1 1
3 3 3
   2 2 3 2
n AG  x  y  z  0 
 1 3 1 3 1 3 1 则n (1,0,1)………………………12分
 1

n AE  x z  0
1 1 1
*数学答案(共 9 页)第 6 页
{#{QQABaQSEggiIAAJAAQgCAw16CAAQkAACAKoOxAAAsAABCQFABAA=}#} 
  nn 78
cosn,n   1  ………………………14分
1 |n||n | 13
1
78
平面AEG与平面APF 所成角的余弦值为 .………………………15分
13
18.证明：线段MN的中点为定点．

 S 2ab 4 a 2
  A 1 B 1 A 2 B 2 
【详解】（1）由题意可得a2 b2 c2 ，解得b1 ，
 

c 3 c 3
e 
 a 2
x2
所以椭圆方程为  y2 1.………………………5分
4
（2）由题意可知：直线PQ的斜率存在，设PQ:y k  x2 1,P  x ,y  ,Q  x ,y ，
1 1 2 2
y k  x2 1
联立方程  x2 ，消去y得：  4k2 1  x2 8k  12k  x16  k2 k  0 ，
  y2 1
 4
则Δ0，解得k 0，
 
8k  12k  16 k2 k
可得x x  ,x x  ，………………………8分
1 2 4k2 1 1 2 4k2 1
y 1
因为B  0,1  ，则直线BP:y  1 x1，
1 1 x
1
2x  2x   2x 
令 y 1，解得x  1 ，即M 1 ,1 ,同理可得M 2 ,1，………………………12分
y 1  y 1   y 1 
1 1 2
2x 2x
1  2
则 y 1 y 1 x x
1 2  1  2
2 kx 2k kx 2k
1 2
x (kx 2k)x (kx 2k) 2kx x 2k(x x ) 16k2
 1 2 2 1  1 2 1 2  4 ………………………16分
(kx 2k)(kx 2k) k2x x 2k2(x x )4k2 4k2
1 2 1 2 1 2
所以线段MN的中点是定点 4,1  .………………………17分
*数学答案(共 9 页)第 7 页
{#{QQABaQSEggiIAAJAAQgCAw16CAAQkAACAKoOxAAAsAABCQFABAA=}#}(x1)(ex x)
19.（1）定义域为x(0,)，h(x)
x2
所以函数h(x)在(0,1)上单调递减，(1,)上单调递增，……………………………….2分
h(x)的最小值为h(1)e1a，
x0时，h(x)；x，h(x)
h(x)有两个零点，只需要h(1)e1a0，即a e1……………………………………….4分
实数a的取值范围为(e1,) ……………………………………….5分
ex 1 ex 2 x x
（2）因为a   ，取对数可得：x lnx  x lnx  2 1 1………………………7分
x x 1 1 2 2 lnx lnx
1 2 2 1
x x x x x x x
下证： x x  2 1 即证明：ln 2  2 1  2  1
1 2 lnx lnx x x x x x
2 1 1 1 2 1 2
x 1
令t  2 1，即证：2lnt t ………………………9分
x t
1
1 t2 2t1
令g(t)2lntt ,g(1)0,g(t) 0
t t2
所以g(t)在(1,)上单调递减,g(t) g(1)0恒成立
.
因此x x 1得证.……………………………………….10分
1 2
3
（3）要证：以AB为直径的圆与直线 y  (x1)恒有公共点
4
3 x x 3
1 2 
4 2 4 x x
即证：  2 1
19 2
4
也就是证明：16(x x )2 12(x x )1276x x 0 ……………………………………….12分
1 2 1 2 1 2
由（2）可知x x 1，所以
1 2
16(x x )2 12(x x )1276x x 16(x x )2 12(x x )880
1 2 1 2 1 2 1 2 1 2
即4  4(x x )11  (x x 2)0
1 2 1 2
*数学答案(共 9 页)第 8 页
{#{QQABaQSEggiIAAJAAQgCAw16CAAQkAACAKoOxAAAsAABCQFABAA=}#}11
下面证明：x x  成立即可
1 2 4
ex(x1)
因为 f(x) ,x(,0)(0,)，因此 f(x)的单调递增区间为(1,)，单调递减区间为(,0),(0,1)，
x2
所以0 x 1 x ，
1 2
x ex 1 ex 2 lnt tlnt (t 1)lnt
令t  2 ,  ,x  ,x  ,t 1x  x  ………………………13分
x x x 1 t 1 2 t 1 1 2 t 1
1 1 2
1
(2lntt )
(t1)lnt
令(t) ,(t) t
t1 (t1)2
1 t2 2t1
令g(t)2lntt ,g(1)0,g(t) 0
t t2
所以g(t)在(1,)上单调递减,g(t) g(1)0恒成立
.
因此(t)0恒成立，(t)单调递增；
当a越大时，t越大，因此x x 的值越大.………………………15分
1 2
1
当a5时，因为 f( )4e0.25 50, f(2.5)0.4e2.550，
4
11
所以1 x 0.25,x 2.5,x x  ，
1 2 1 2 4
11
所以a5是，x x  ………………….17分
1 2 4
*数学答案(共 9 页)第 9 页
{#{QQABaQSEggiIAAJAAQgCAw16CAAQkAACAKoOxAAAsAABCQFABAA=}#}