2024年河南五市数学参考答案_2024年3月_013月合集_2024届河南省五市高三下学期第一次联考_2024年河南五市高三第一次联考数学试题+答案

年河南省五市高三第一次联考 2024 （数学）参考答案 一、选择 : 题号 1 2 3 4 5 6 7 8 答案 C C C B D A B A 二、选择 : 题号 9 10 11 12 答案 ABD BCD AB BD 三、填空 : 2 39 13. 1 14. 60 15. 1012 16. 13 四、解答题 : 17.(Ⅰ)由条件b2 a2 ac，根据正弦定理可得 sin2 Bsin2 Asin AsinC ...........................................1 分 即cos2Acos2B 2sin AsinC .......................................2分 所以2sin(AB)sin(AB)2sin AsinC ..............................3 分 也即sin(BA)sin A...............................................4分 从而证得B 2A...................................................5 分 (Ⅱ)若ABC为锐角三角形，根据(Ⅰ)B 2A     B 2A 2A    2  2 则       C AB 3A  2  2   得  A ......................................................6分 6 4 sin(CA)sinB sin(ABA)sinB sin4Asin2A 式子   sin A sin A sin A 数学参考答案 第 1 页 共 7 页 {#{QQABZYQAggiAAoBAAAgCAQnwCEIQkAACACoOgBAEMAAACRNABAA=}#}sin(3A A)sin(3AA)   2cos3A.....................................................................8 分 sin A  3 2 由 3A cos3A( ,0) 2 4 2 sin(CA)sinB 因此 2cos3A( 2,0)即为所求.........................................10 分 sin A a 18.(Ⅰ)根据条件则 f '(x) 2x(x 0)...............................1分 x 当a0时， f '(x)0在定义域(0,)内恒成立， 因此 f(x)在(0,)递减；...............................2分 2a 当a 0时，由 f '(x)0，解得0 x ； 2 2a f '(x)0，解得x .................................3分 2 因此： 当a0时， f(x)的单调减区间为(0,)，无增区间； 2a 2a a 0时，f(x)的单调减区间为( ,)，增区间为(0, )；..........4 分 2 2 2a 注：区间端点x 处可以是闭的 2 (Ⅱ)若 f(x)有两个零点，有(Ⅰ)可知a 0 2a 且 f(x) f( ) 2 2a 2a 2a 则必有 f( )aln ( )2a 0 .............................6分 2 2 2 a 即ln 10 2 2 解得a  ........................................................8分 e 1 1 又因 f( ) 0, f(4a)aln4a16a2 aa(ln4a16a1).......................9 分 e e2 8 1 14t 即g(t)lnt4t1(t 4a  )g'(t) 4 e t t 数学参考答案 第 2 页 共 7 页 {#{QQABZYQAggiAAoBAAAgCAQnwCEIQkAACACoOgBAEMAAACRNABAA=}#}1 1 可得g(t) g( )ln 110， 4 4 8 也即得g(t)0在t( ,)恒成立....................................................................10 分 e 1 2a 2a 从而可得 f(x)在( , ),( ,4a)区间上各有一个零点...............11分 e 2 2 2 综上所述，若 f(x)有两个零点实数a的范围为( ,)..................12分 e 19.(Ⅰ)记等差数列 a 的公差为d ，则由条件 n a a a a 2d a 3d a 10d 3 4 11 1 1 1 3(a 5d)3a 84 1 6 得a 28.........................................................2 分 6 从而d a a 7 6 33285.................................................3分 a a (n6)d n 6 5n2 即为所求...................,..........................4分 (Ⅱ)对任意nN ，由5k a 52k ，即5k 5n252k ..................5分  n 2 2 整理得5k1  n52k1 .........................................6 分 5 5 故5k11n52k1，...............................................8分 从而得b 52k15k1...............................................9 分 k 则 b 的前k项和为 k 5(25k 1) 1(5k 1) T   ..........................................10分 k 251 51 1  (52k165k 1)(k N ) .......................................12分  24 20.(Ⅰ) 取BC中点为E,由条件则OE为梯形ABCD的中位线， 数学参考答案 第 3 页 共 7 页 {#{QQABZYQAggiAAoBAAAgCAQnwCEIQkAACACoOgBAEMAAACRNABAA=}#}则OE  BC .............................................................................................................1 分 又PB  PC ,则PE  BC 且PEOE  E ,根据线面垂直的判定定理可得BC 面POE.............2分 得BC  PO.......................................................3分 又由PAPD,则PO  AD,AD,BC 为梯形的两腰，则AD与BC相交 即可得PO 面ABCD，.............................................5分 又OC 面ABCD,进而得CO  PO...................................6分 1 (Ⅱ)取CD的中点为Q,由AB  CD 1,CDA60, 2 则AQ CD,AD CD  2QD  2, 因此ACD为等边三角形,CO  AD 由(Ⅰ)知PO 面ABCD，OP OAOC ..............................7分    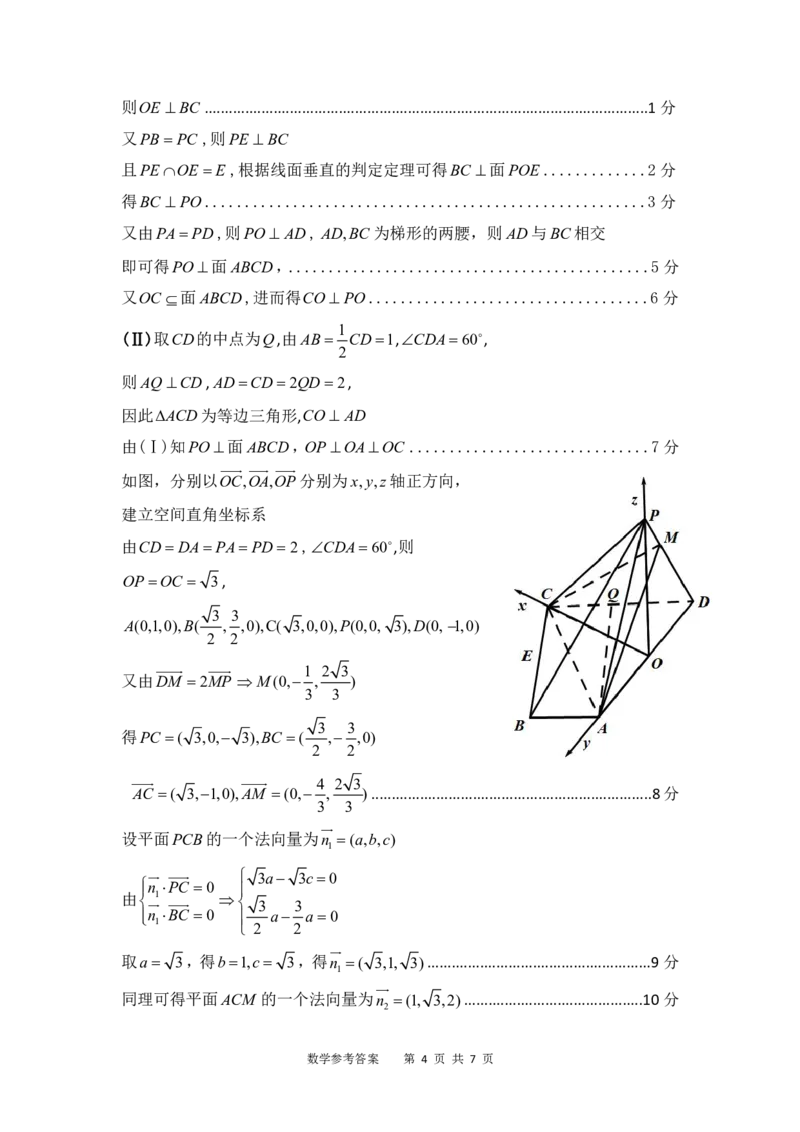如图，分别以OC,OA,OP分别为x,y,z轴正方向， 建立空间直角坐标系 由CD  DA PA PD  2,CDA60,则 OP OC  3, 3 3 A(0,1,0),B( , ,0),C( 3,0,0),P(0,0, 3),D(0, 1,0) 2 2   1 2 3 又由DM 2MP  M(0, , ) 3 3 3 3 得PC ( 3,0, 3),BC ( , ,0) 2 2   4 2 3 AC ( 3,1,0),AM (0, , ).....................................................................8分 3 3  设平面PCB的一个法向量为n (a,b,c) 1    3a 3c0  n PC 0  由  1   3 3 n BC 0  a a 0 1  2 2  取a  3，得b1,c 3，得n ( 3,1, 3).......................................................9 分 1  同理可得平面ACM 的一个法向量为n (1, 3,2)............................................10分 2 数学参考答案 第 4 页 共 7 页 {#{QQABZYQAggiAAoBAAAgCAQnwCEIQkAACACoOgBAEMAAACRNABAA=}#}记平面PCM 与平面ACM 所成的角的大小为，   n n 311 32 3 则cos| 1 2 | .......................................................11 分 |n ||n | 7 8 1 2 42  ........................................................................................................12 分 7 21.(Ⅰ)由条件，每次抢题+答题，甲得1分的概率为 1 3 1 1 11 P      ..............................................1分 甲 2 5 2 2 20 11 9 每次抢答题乙得1分的概率为P 1P 1  ...................2分 乙 甲 20 20 若第二题答完比赛结束，则前两次答题甲得2分或者乙得2分，因此第二题发完 11 9 101 比赛结束事件发生的概率P（ ）2（ ）2  .................................................4分 20 20 200 (Ⅱ)根据题意，竞赛结束时抢答题目的总数 X 的所有可能取值为 2,4,6,8，，2n，(nN ) ...........................................5分  记 p  P(X 2n) n 101 由(Ⅰ)知，当X 2时， p  P(X 2) ， 1 200 99 且 p  p (nN ).............................................7分 n1 200 n  则X 的分布列可表示为： X 2 4 6 … … 2n … … P p p p … … p … … 1 2 3 n ...............................................8分 ∴EX 2p 4p 6p 8p 2np  1 2 3 4 n 101 99 99 99 99  4 p 6 p 8 p 2n p  100 200 1 200 2 200 3 200 n1 101 99   (4p 6p 8p 2n p (2n2) p ) 100 200 1 2 3 n1 n 101 99   [(2p 4p 6p 2n p )2(p  p  p  p )] 100 200 1 2 3 n 1 2 3 n 101 99   (EX 2)...........................................11分 100 200 400 解得EX  ....................................................12分 101 数学参考答案 第 5 页 共 7 页 {#{QQABZYQAggiAAoBAAAgCAQnwCEIQkAACACoOgBAEMAAACRNABAA=}#}22.(Ⅰ)根据条件则2a 6,a 3, 当点D位于短轴顶点时，DFF 面积的最大，且(S ) bc 2 2 ， 1 2 DFF max 1 2 也即a2 b2 c2 9,bc  2 2 ........................................2分 解得b2 2,c1或b1,c2 2 1 又e ，因此a 3,b1,c2 2 ，...................................3分 3 x2 E:  y2 1 .....................................................4分 9 3 1 85 (Ⅱ)存在定点Q( , )使得|QH | 为定值.....................5分 2 3 6 由题意过点P的直线l 与椭圆E交于A点，与直线x8交于M 点,l 与椭圆 1 2 E交于B点，与直线x8交于N 点,设A(x ,y ),B(x ,y ),M(8,t ),N(8,t ). 1 1 2 2 1 2 根据条件则t t 11， 1 2  y t 1  1  x 3 11 y y t t 且  1  1  2  1  2 1 ①..........................6分 y t x 3 x 3 11 11  2  2 1 2  x 3 11 2 由条件则直线AB的斜率不为0，因此设直线AB的方程为 l :x myn AB y y y (x 3)y (x 3) y (my n3)y (my n3) 由①则 1  2  1 2 2 1  1 2 2 1 x 3 x 3 (x 3)(x 3) (my n3)(my n3) 1 2 1 2 1 2 2my y (n3)(y  y )  1 2 1 2  1 ② m2y y m(n3)(y  y )(n3)2 1 2 1 2 .....................................................7 分 x2   y2 1 联立 9 ，整理得(m2 9)y2 2mnyn2 90 ，该方程有两个不同的实  xmyn 数根y ,y ，则4m2n24(n29)(m29)0 ，由韦达定理可得 1 2 数学参考答案 第 6 页 共 7 页 {#{QQABZYQAggiAAoBAAAgCAQnwCEIQkAACACoOgBAEMAAACRNABAA=}#}2mn n29 y  y  ,y y  ........................................8分 1 2 m2 9 1 2 m2 9 代入②中 18m6mn 整理得 1，又n3， 9(n3)2 3 化简得m (n3)...............................................9分 2 3 3 3 因此l :x myn  (n3)yn n(1 y) y AB 2 2 2 2 即直线AB过定点(3, )...........................................10 分 3 2 记直线AB过定点为R(3, ) 3 过原点O作直线AB的垂线，垂直为H ，则点H 在以OR为直径的圆上，则OR的 1 85 中点到 H 的距离等于 |OR| 为定值，因此存在定点即为OR 的中点 2 6 3 1 1 85 Q( , )使得|QH| |OR| 为定值...............................12分 2 3 2 6 数学参考答案 第 7 页 共 7 页 {#{QQABZYQAggiAAoBAAAgCAQnwCEIQkAACACoOgBAEMAAACRNABAA=}#}