浙江省台州市2023-2024学年高二下学期6月期末考试数学试题_6月_240630浙江省台州市2023-2024学年高二下学期6月期末试题

台州市 2023 学年第二学期高二年级期末质量评估试题
数学
2024.6
一、单项选择题：本题共 8小题，每小题 5分，共40分。在每小题给出的四个选项中，只有
一项是符合题目要求的。
1．集合A  x x3  ，集合B  2,3,4,5 ，则AB （ ）
A．  x x3  B． 2,3  C． 2,3,4,5  D．  x x3或x 4或x 5 
2．复数z及其共轭复数z 满足z2z 32i（其中i是虚数单位），则z （ ）
2 2
A．3 i B．3 i C．12i D．12i
3 3
    
3．已知向量a  1,x ，b x,4 ，xR．若  ab  ∥b，则x（ ）
A．2 B．2或2 C．4 D．4或1
4 1
4．已知a，b为正实数，  1，则（ ）
a2 b2
A．ab的最小值为4 B．ab的最大值为4
C．ab的最小值为2 D．ab的最大值为2

5．设定义在R 上的函数 f  x sin2x ．记 f
1
 x  f  x ，对任意的nN*， f
n1
 x  

f
n
 x 

，则
f  x （ ）
2024
A．sin2x B．cos2x C．22023cos2x D．22024sin2x
6．甲、乙等5人站成前排2人、后排3人拍照，其中甲、乙两人在同一排相邻的排法共有（ ）
A．12种 B．24种 C．36种 D．48种
7．现有2道单选题，假定学生张君对每道题有思路与无思路的概率均为0.5．他对题目若有思路，做对的
概率为0.75；若没有思路，做对的概率为0.25．在已知张君恰做对1题的条件下，则其恰有1题有思路的
概率为（ ）
7 1 9 5
A． B． C． D．
16 2 16 8
8．设 f  x a x3a x2a xa （a ，a ，a ，a R且a 0），方程 f  x 0在复数集C内的三
3 2 1 0 0 1 2 3 3
个 根 为 x ， x ， x ， 可 以 将 上 述 方 程 变 形 为 a  xx  xx  xx  0 ， 展 开 得 到
1 2 3 3 1 2 3
a x3a  x x x  x2 a  x x x x x x  xa x x x  0，比较该方程与方程 f  x 0，可以得
3 3 1 2 3 3 1 2 2 3 3 1 3 1 2 3
a a a
到x x x  2 ，x x x x x x  1 ，x x x  0 ．已知 f  i 1i（i是虚数单位），且tan，
1 2 3 a 1 2 2 3 3 1 a 1 2 3 a
3 3 3
学科网（北京）股份有限公司tan，tan是 f  x 0的三个实根，则tan （ ）
A．1 B．1 C．2 D．2
二、多项选择题：本题共 3小题，每小题 6分，共18分。在每小题给出的四个选项中，有多
项是符合题目要求的。全部选对得 6分，部分选对得部分分，有选错的得 0分。
9．下列命题正确的是（ ）
 1 2
A．若随机变量X服从二项分布B5, ，则D  X 
 3 9
B．若随机变量X服从正态分布N  5,4 ，则P  X 7 P  X 3 1
C．当事件A，B，C两两独立时，P  ABC P  A  P  B  P  C 
D．当事件A，B，C两两互斥时，P  ABC P  A P  B P  C 
10．关于函数 f  x  x3的图象的切线，下列说法正确的是（ ）
A．在点A  1,1 处的切线方程为 y 3x2
B．经过点A  1,1 的切线方程为 y 3x2
C．切线l:y kxb  k 0 与y  f  x 的图象必有两个公共点
D．在点P  x ,x3 处的切线过点Q  x ,x3 x  x ，则x 2x
1 1 0 0 0 1 0 1
1
11．已知△ABC 的内角A，B，C所对的边分别为a，b，c，其中a为定值．若△ABC 的面积S  a2，
2
则（ ）
4
A．tanA的最大值为
3
B．b2 c2的最小值为2a2
 
C．△ABC周长的最小值为 51 a
b  51 51
D． 的取值范围是 , 
c  2 2 
三、填空题：本题共 3小题，每小题 5分，共15分。
12． x2y 5 的展开式中x3y2的系数是______（用数字作答）·
 π 2 2 1
13 ． 已 知  ，  0,  ， sin  ， coscos ， 则 tan  ______ ，
 2 3 4
cos
______．
学科网（北京）股份有限公司14．在正方体ABCDABC D 中，P为正方形ADD A 的中心，直线l 底面ABCD，则二面角A lP
1 1 1 1 1 1 1
的平面角的正弦值的最大值是______．
四、解答题：本小题共5小题，共 77分。解答应写出文字说明、证明过程或验算步骤。
15．（13分）
 π
已知函数 f  x 2sin x  0,0 ，xR ．给出如下三组条件：
 2
5π
①函数 f  x 的最小正周期为π，且当x 时， f  x 取到最大值；
12
 7π π   π 5π
②函数 f  x 的单调递减区间是 kπ ,kπ  kZ ，单调递增区间是 kπ ,kπ  kZ ；
   
 12 12  12 12
π π   π 
③x ，x 是方程 f  x 1的两个根， x x 的最小值为 ，且 f  x  f  x  0．
1 2 1 2 3 6  6 
从这三组条件中任选一组作为条件，完成以下问题：
（Ⅰ）求函数 f  x 的解析式；
 x π 2  5π
（Ⅱ）若 f  0    ，求 f x  的值．
 2 6 3  0 12
注：如果选择多组条件分别解答，按第一组解答给分．
16．（15分）
1
已知函数 f  x  xa  为偶函数．
xa
（Ⅰ）求实数a的值；
（Ⅱ）若不等式 f  x bx恒成立，求实数b的取值范围．
17．（15分）
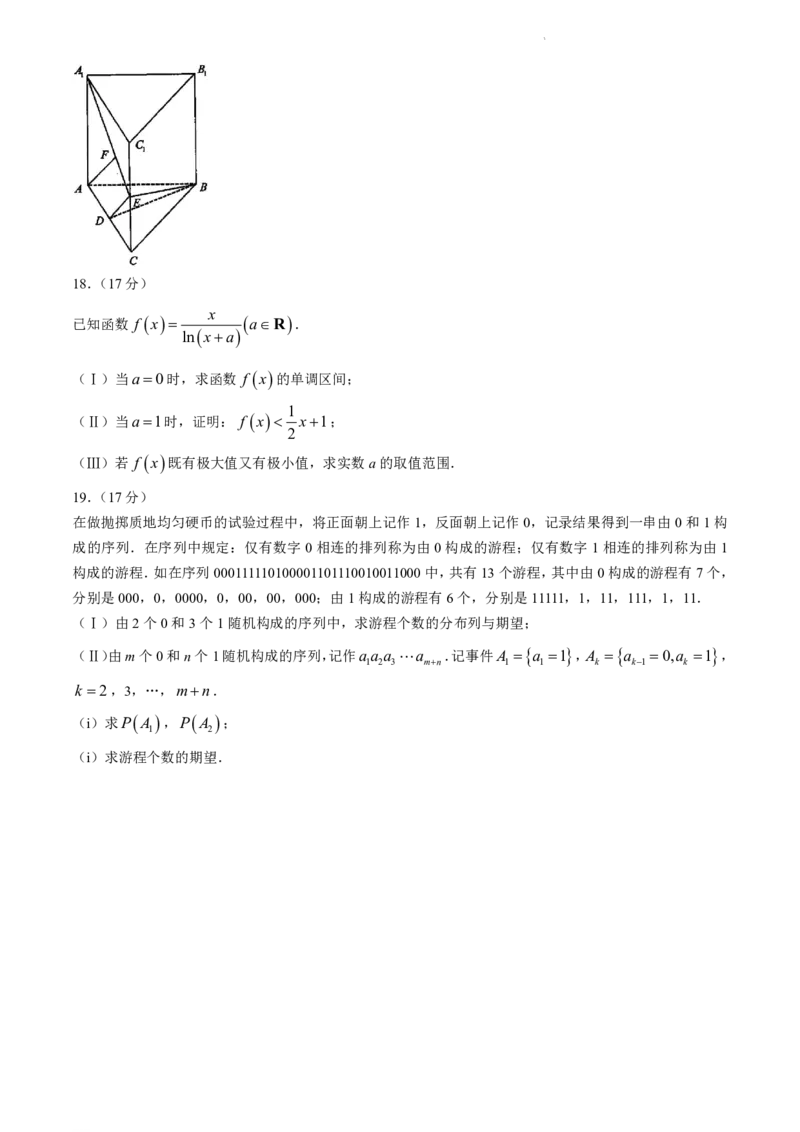
如图，在直三棱柱ABCABC 中，AB  BC，AB BB  2，BC 2 3．D，E分别是棱AC 、CC
1 1 1 1 1
的中点，点F在线段AE上．
1
 
（Ⅰ）若AF 2FE ，求证：AF∥平面BDE；
1
3
（Ⅱ）若三棱锥F ABD的体积为 ，求直线BF 与平面AACC 所成角的正切值．
2 1 1
学科网（北京）股份有限公司18．（17分）
x
已知函数 f  x   aR ．
ln  xa 
（Ⅰ）当a0时，求函数 f  x 的单调区间；
1
（Ⅱ）当a 1时，证明： f  x  x1；
2
（Ⅲ）若 f  x 既有极大值又有极小值，求实数a的取值范围．
19．（17分）
在做抛掷质地均匀硬币的试验过程中，将正面朝上记作1，反面朝上记作0，记录结果得到一串由0和1构
成的序列．在序列中规定：仅有数字0相连的排列称为由0构成的游程；仅有数字1相连的排列称为由1
构成的游程．如在序列000111110100001101110010011000中，共有13个游程，其中由0构成的游程有7个，
分别是000，0，0000，0，00，00，000；由1构成的游程有6个，分别是11111，1，11，111，1，11．
（Ⅰ）由2个0和3个1随机构成的序列中，求游程个数的分布列与期望；
（Ⅱ）由m个0和n个1随机构成的序列，记作aa a a ．记事件A  a 1 ，A  a 0,a 1 ，
1 2 3 mn 1 1 k k1 k
k 2，3，…，mn．
（i）求P  A ，P  A ；
1 2
（i）求游程个数的期望．
学科网（北京）股份有限公司