2024重庆市巴蜀中学高三4月适应性月考卷（八）数学(1)_2024年4月_024月合集_2024届重庆市巴蜀中学高三4月适应性月考卷（八）

}#}=AABANRyAAAoIABwOoKCAEAkQEgCgFQUCgBAABIQgAggUQQRBAQQ{#{}#}=AABANRyAAAoIABwOoKCAEAkQEgCgFQUCgBAABIQgAggUQQRBAQQ{#{数学参考答案 一、单项选择题（本大题共8小题，每小题5分，共40分） 题号 1 2 3 4 5 6 7 8 答案 C B D A B C B D 【解析】 1．因为B A，故2aA． ①当2aa时，a0，则A{0，1，1}，故a0不成立；②当 1 2aa2 1时，解得a1，则A{1，2，1}，故a1不成立；③当2a1时，即a ，则 2 1 5  1 1 A ， ，1，B{1}，故a 成立，故a ，故选C． 2 4  2 2 3 10 10 1 2．因为(0，π)，cos ，故sin ，故tan ，故选B． 10 10 3 1 1 5 3．因为a 3，令{a }的公差为d，则a a  a a d a 2d  (a 3d) a 5， 6 n 5 8 3 9 6 6 3 6 3 6 故选D． 4．间接法：总的辩论队数量是C4 126，全是男生的辩论队数量是：C4 5，全是女生的辩 9 5 论队数量是C4 1，故满足的辩论队数量是：C4 C4 C4 12651120，故选A． 4 9 5 4 π  3 π  3 π 5．①当PFF  时，P1，  ；②当PF F  时，P1，  ；③当FPF  时， 1 2 2  2 2 1 2  2 1 2 2 无解，故一共满足要求的P点个数是4，故选B． 6．因为 lnaln3ln7， lnbln4ln6 ， lncln5ln5， lnd ln4ln6 ，则 d b ，故 |d b|0，又|ba|0，|cb|0，|d c|0，|ca|0，|d a|0，故最小值是|d b|， 故选C． 7．令t x2，则g(t)atlnt1，当a0时，g(t)lnt1与x轴有公共点，故a0时不 成立；当a0时，g(ea)aea a1a(ea 1)10，又g(e)ae0，故g(t)atlnt1 与x轴有公共点，故a0时不成立；当a0时，g(1)a1，因为g(t)atlnt1与x轴 lnt1 lnt1 没有公共点，故t(0，)时，atlnt10恒成立，即a 恒成立，令h(t) ， t t 数学参考答案·第1页（共9页） {#{QQABRQQUggAgQIBAABgCUQFgCgEQkAEACKoOwBAIoAAAyRNABAA=}#}2lnt h(t) ，t(0，e2)时，h(t)0，t(e2，)时，h(t)0，故h(t)在(0，e2)上单 t2 1 1 调递增，在(e2，)上单调递减，故h(t)≤h(e2) ，故a ，故选B． e2 e2 8．因为OQa，OF c，又因为P，Q在渐近线上，故OQFQ， FQb，又OM FP， 1 1 1 1   MP OP t a 且5MPFM ，设MPt，则FP6t，Rt△PMO∽Rt△PQF ，故  ，则  ， 1 1 1 PQ PF 2a 6t 1 b2 故6t2 2a2，又在Rt△PQF 中：PF2 QF2 PQ2，即36t2 12a2 4a2 b2，解得 8， 1 1 1 a2 则e2 9，解得e3，故选D． 二、多项选择题（本大题共 3 小题，每小题 6 分，共 18 分． 在每小题给出的选项中，有多 项是符合题目要求的，全部选对的得6分，部分选对的得部分分，有选错的得0分） 题号 9 10 11 答案 ABC AC ABD 【解析】 1 1 9．根据正态分布的定义得P(X≤) ，故 A 正确；E(X)2，E(Y)4 2，故 2 2 1 1 E(X)E(Y)，故B正确；D(X)2 1， D(Y)4  1，故D(X)D(Y)，故C正 2 2 1 4 1 确；P(Y 1)C1    ，故D错误，故选ABC． 4 2 4 10．根据正方体的性质得AC BC，故A正确；当r 1时，球O 与正方体内切，当O 与正 1 1 1 1 2 方体的三个面相切时半径r 最大，此时满足1 3r  3r 2 3，解得r 2 3，故 2 2 2 2 B错误；对任意的球O ，球O 与正方体的三个面相切时半径r 最大，故当球O ，球O 都 1 2 2 1 2 与正方体的三个面相切时 r r 取最大值，即 r  3r r  3r 2 3 ，解得 1 2 1 1 2 2 r r 3 3，故r r 的最大值是3 3，故选项C正确；由选项B和选项C知，r r 1 2 1 2 1 2 取最大值3 3，此时2 3≤r≤1，则4π(r2 r2)4πr2 4π(3 3r)2，当r 2 3 1 1 2 1 1 1 或r 1取得最大值(3216 3)π，故选项D错误，故选AC． 1 11． f(x，y，1)0对应曲线是x2  y2 10表示单位圆，故A正确； f(x，y，2)0对应的曲 线是x4  y4 10，故1≤x≤1，1≤y≤1，且|x|1与|y|1不能同时取等号，故S 4， 2 故选项B正确；f(x，y，n)0对应的曲线x2n  y2n 1，令|x|n|x|，| y|n| y|，因为曲 数学参考答案·第2页（共9页） {#{QQABRQQUggAgQIBAABgCUQFgCgEQkAEACKoOwBAIoAAAyRNABAA=}#}1 1 线 (x)2 (y)2 1 ，则 |x||x|n ，且 |y||y|n ， f(x，y，n1)0(n≥2) 对应的曲线 1 x2n2  y2n2 1，令|x|n1|x|，| y|n1| y|，因为曲线(x)2 (y)2 1，则|x||x|n1，且 1 1 1 1 1 |y|| y|n1，又|x|n≥|x|n1，|y|n≥|y|n1且等号不能同时取得，故S S ，故{S } n n1 n 是单调递增的，故选项C是错误的； f(x，y，2)0对应的曲线是x4  y4 10，假设曲  π 线 上 任 意 一 点 P(x，y )， 则 x4  y4 1 ， 令 x2 cos，y2 sin0≤≤  ， 则 0 0 0 0  2 1 d2 x2  y2 sincos≤ 2，故d≤4 2 24，故选项D正确，故选ABD． 0 0 三、填空题（本大题共3小题，每小题5分，共15分） 题号 12 13 14 答案 3i 2 (5， 57] 【解析】 12．因为z(1i)24i，则z(1i)(1i)(24i)(1i)，即2z62i，则z3i，故答案是 z3i. 3  3  13．因为 f  x f  x ，即 f(x) f(3x)，又 f(x) f(6x)0，即 f(3x) f(3x) 2  2  0，故 f(x3)f(x)，故 f(x6) f(x)，则 f(2024) f(2) f(1)2，故答案是2． 1 π 2 2 a 2 2 14．因为cosA ，且0 A ，故sinA ，由正弦定理得：2R  3， 3 2 3 sinA 2 2 3 故2bc2R(2sinBsinC)3[2sin(AC)sinC]3[2sinAcosC2cosAsinCsinC] 4 2 5  π 3 cosC sinC5sinC4 2cosC．因为△ABC是锐角三角形，故0C ， 3 3 2   π 1 且 AC  ， 故 cosAsinC1， 即 sinC1 ， 又 2bc5sinC4 2cosC 2 3 1 π  π   57sin(C) ，令锐角满足sin ，故C ，C，  ，且 3 2  2  π  π π π   ，故sin(C) 在 ，  上单调递增，在  ，  上单调递减，故 2  2 2 2  数学参考答案·第3页（共9页） {#{QQABRQQUggAgQIBAABgCUQFgCgEQkAEACKoOwBAIoAAAyRNABAA=}#}π 1 C 时，2bc取得最大值 57 ．又sinC  时，2bc5sinC4 2cosC 7， 2 3 又当sinC 1时，2bc5sinC4 2cosC 5，故2bc的取值范围是(5， 57]. 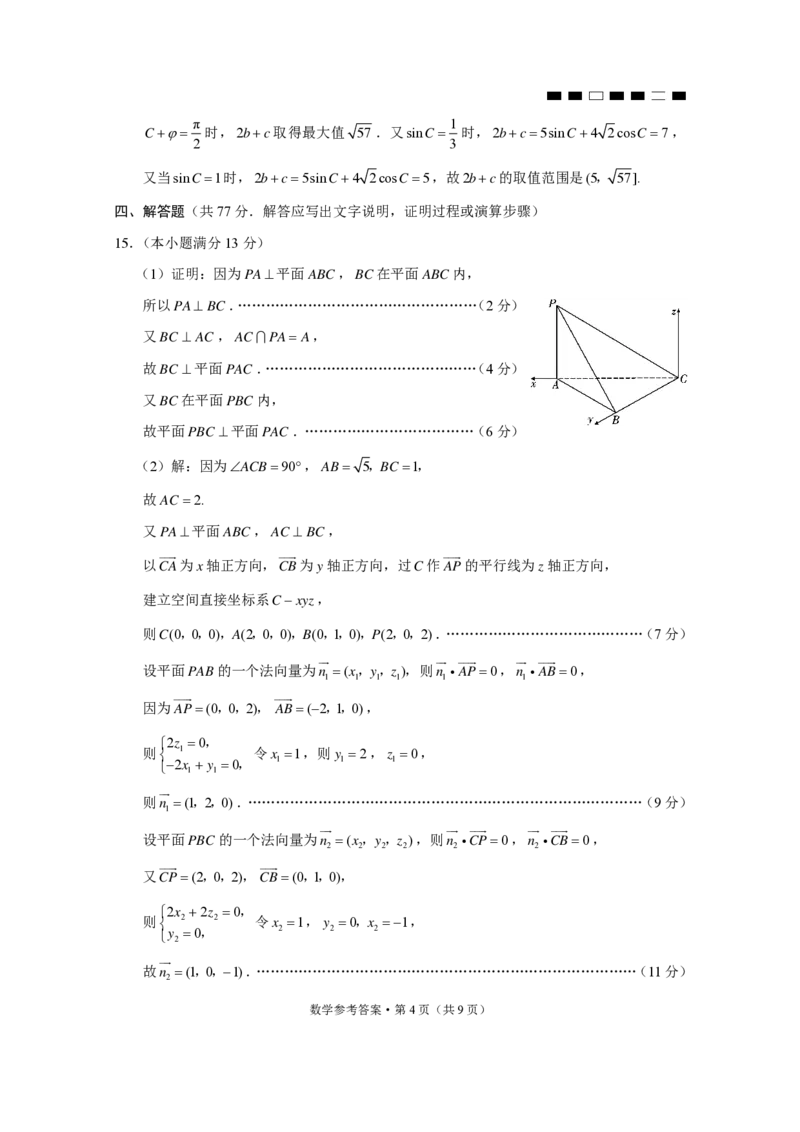四、解答题（共77分．解答应写出文字说明，证明过程或演算步骤） 15．（本小题满分13分） （1）证明：因为PA平面ABC，BC在平面ABC内， 所以PABC．……………………………………………（2分） 又BC  AC，ACPA A， 故BC 平面PAC ．………………………………………（4分） 又BC在平面PBC 内， 故平面PBC 平面PAC ．………………………………（6分） （2）解：因为ACB90，AB 5，BC 1， 故AC2. 又PA平面ABC，AC BC，    以CA为x轴正方向，CB为y轴正方向，过C作AP的平行线为z轴正方向， 建立空间直接坐标系Cxyz， 则C(0，0，0)，A(2，0，0)，B(0，1，0)，P(2，0，2)．……………………………………（7分）      设平面PAB的一个法向量为n (x，y，z )，则n  AP0，n  AB0， 1 1 1 1 1 1   因为AP(0，0，2)， AB(2，1，0)， 2z 0， 则 1 令x 1，则y 2，z 0， 2x  y 0， 1 1 1 1 1  则n (1，2，0)．…………………………………………………………………………（9分） 1      设平面PBC 的一个法向量为n (x，y，z )，则n CP0，n CB0， 2 2 2 2 2 2   又CP(2，0，2)，CB(0，1，0)， 2x 2z 0， 则 2 2 令x 1，y 0，x 1， y 0， 2 2 2 2  故n (1，0，1)．………………………………………………………………………（11分） 2 数学参考答案·第4页（共9页） {#{QQABRQQUggAgQIBAABgCUQFgCgEQkAEACKoOwBAIoAAAyRNABAA=}#}    n n 1 10 故n 与n 夹角的余弦值cos 1 2   ， 1 2 |n ||n | 5 2 10 1 2 3 10 3 10 故sin ，故二面角APBC的正弦值sin ． 10 10 ………………………………………………………………………………………（13分） 16．（本小题满分15分） 解：（1）因为 f(x)ex(x2 x1)， 则 f(x)ex(x2 x12x1)ex(x2 x)，……………………………………………（1分） 故当x(，1)时， f(x)0， 当x(1，0)时， f(x)0，当x(0，)时， f(x)0， ………………………………………………………………………………………（3分） 则 f(x)在区间(，1)上单调递增，在区间(1，0)上单调递减，在区间(0，)上单调 递增， 故 f(x)的单调递增区间是(，1)，(0，)，单调递减区间是(1，0)， ………………………………………………………………………………………（4分） 3 故 f(x)在x1处取得极大值 f(1) ，在x0处取得极小值 f(0)1． e ………………………………………………………………………………………（6分） （2）设切点M(x，ex0(x 1))， 0 0 因为g(x)(x1)ex，则g(x)xex，…………………………………………………（7分） (x 1)ex0 m 则切线的斜率k x ex0  0 ， 0 x 0 0 化简得：mex0(x2 x 1)．…………………………………………………………（8分） 0 0 因为过点P(0，m)可以作三条直线与曲线yg(x)相切， 故mex0(x2 x 1)有三个不同的实根，即 f(x)m0有三个零点． 0 0 ………………………………………………………………………………………（9分） 令h(x) f(x)m，则h(x) f(x)， 由（1）知：则h(x)在(，1)上单调递增，在(1，0)上单调递减，在(0，)上单调递 增，………………………………………………………………………………………（10分） 3 又h(1) m，h(0)1m． e 数学参考答案·第5页（共9页） {#{QQABRQQUggAgQIBAABgCUQFgCgEQkAEACKoOwBAIoAAAyRNABAA=}#}3 ①当h(1) m0时，x(，0)时，h(x)0，故h(x)至多一个零点，不满足； e ②当h(0)1m0时，x(1，)时，h(x)0，故h(x)至多一个零点，不满足； 3 ③当h(1) m0，x(，0)时，h(x)有唯一零点x1，h(x)在(0，)上单调 e 递增，故h(x)在区间(0，)至多一个零点，故h(x)至多两个零点，不满足； ④当h(0)1m0，x(1，)时，h(x)有唯一零点x0，h(x)在(，1)上单调 递增，故h(x)在区间(，1)上至多一个零点，故h(x)至多两个零点，不满足； 3 3 ⑤当h(1) m0，h(0)1m0，即 m1时， e e 13 3 因为h(3) m1m0，h(1)em m0， e3 e 故存在x (3，1)，x (1，0)，x (0，1)使得h(x)0，i1，2，3， 1 2 3 i 3 故 m1成立， e 3 综上所述：实数m的取值范围是 m1．………………………………………（15分） e 17．（本小题满分15分） 解：（1）用A表示甲投篮命中，A表示甲投篮未命中， 用B表示乙投篮命中，B表示乙投篮未命中， 记甲同学连续投篮了三次并赢得了比赛的事件为M ，………………………………（2分） 1 1 1 7 则P(M)P(AAA)P(AAAB)P(AAABB)    ． 8 16 32 32 ………………………………………………………………………………………（5分） 1 （2）①剩余两次投篮，甲、乙比分3∶0获胜的概率是P P(AAA) ； 1 8 ………………………………………………………………………………………（7分） ②剩余一次投篮，甲、乙比分3∶1获胜的概率是P ： 2 3 1 4 3 P P(AAAB)P(AABA)P(ABAA) (也可用P C1    )； 2 16 2 3 2 16 ……………………………………………………………………………………（10分） 数学参考答案·第6页（共9页） {#{QQABRQQUggAgQIBAABgCUQFgCgEQkAEACKoOwBAIoAAAyRNABAA=}#}③不剩余投篮，前4次投篮甲、乙比分2∶2获胜的概率是P ： 3 6 P P(AAABB)P(AAB AB)P(AABBA)P(ABAAB)P(AB ABA)P(ABBAA) 3 32 1 4 1 6 (也可用P C2     )， 3 4 2 2 32 1 故甲获胜的概率是PP P P  ．………………………………………………（15分） 1 2 3 2 18．（本小题满分17分） 解：（1）当直线AB的斜率为0时不成立， 设AB的直线方程为：xm y4，A(x，y )，B(x，y )， 1 1 1 2 2 ………………………………………………………………………………………（2分） y2 2px， 联立抛物线得： 消去x得：y2 2pm y8p0，故y y 8p． xm y4， 1 1 2 1 ………………………………………………………………………………………（4分） y2 y2 y2y2 64p2 又x  1 ，x  2 ，故x x  1 2  16， 1 2p 2 2p 1 2 4p2 4p2 又OAOB，则xx  y y 0， 1 2 1 2 故168p0，解得 p2，……………………………………………………………（6分） 故抛物线E的方程是：y2 4x．………………………………………………………（7分） （2）因为y2 4x，P(x，2)在抛物线上，故x 1，则P(1，2)． 0 0 ………………………………………………………………………………………（8分） 当直线MN 的斜率为0时不成立， 设MN 的直线为xmy2m4，M(x，y )，N(x，y )，……………………………（9分） 3 3 4 4 y2 4x， 联立抛物线得： 消去x得：y2 4my8m160， xmy2m4， 则y  y 4m，y y 8m16，………………………………………………………（11分） 3 4 3 4 y 2 y 2 4 y 2 y 2 4 因为k  3  3  ，k  4  4  ， 1 x 1 y2 y 2 2 x 1 y2 y 2 3 3 1 3 4 4 1 4 4 4 ……………………………………………………………………………………（14分） 数学参考答案·第7页（共9页） {#{QQABRQQUggAgQIBAABgCUQFgCgEQkAEACKoOwBAIoAAAyRNABAA=}#}4 4 16 16 4 则k k      ， 1 2 (y 2) (y 2) y y 2(y  y )4 8m168m4 3 3 4 3 4 3 4 4 故k k 的值为 ．……………………………………………………………………（17分） 1 2 3 19．（本小题满分17分） 解：（1）a 23 22 20 13， 3 a 23 22 21 14， 4 a 24 2120 19．……………………………………………………………………（3分） 5 （2）6725121605121283229 27 25， 故672A，则672是数列{a }的项；…………………………………………………（5分） n 2024102410001024512488210 29 488210 29 28. 令a 210 29 28，则a 2112120 2051，故a 2024a ， k k1 k k1 故2024不是{a }中的项．………………………………………………………………（8分） n （3）当c2时在集合A中有C2个元素， 2 当c3时在集合A中有C2个元素， 3 …… 当cn时在集合A中有C2个元素， n (n1)n(n1) 则集合A一共有C2 C2 C2 C3  个元素， 2 3 n n1 6 ……………………………………………………………………………………（10分） (n1)n(n1) 故{a }有 项， n 6 当cn时在集合A中的C2个元素中最小的元素是2n 2120， n 最大元素是2n 2n12n2(n≥2)， 故cn的元素在{a }中最大项是2n 2n12n2(n≥2)，最小项是2n 2120； n 1098 令n9，则{a }共有 120项，……………………………………………（12分） n 6 则a 恰好是c9的元素在{a }中的最大项， 120 n 则a 29 28 27 896；……………………………………………………………（13分） 120 数学参考答案·第8页（共9页） {#{QQABRQQUggAgQIBAABgCUQFgCgEQkAEACKoOwBAIoAAAyRNABAA=}#}765 令n6，则一共有 35项， 6 记T 表示集合A中cn的元素之和，则S T T T ， n 35 2 3 6 因为集合A中cn的元素有C2个， n 这些元素中含2n的个数是C2，含20，21，…，2n1的个数都是n1， n ……………………………………………………………………………………（15分） 故T 2nC2 (2n12120)(n1)，则： n n T 22C2 (2120)(21)7， 2 2 T 23C2 (22 2120)(31)382738， 3 3 T 24C2 (23 22 2120)(41)166315141， 4 4 T 25C2 (24 23 22 2120)(51)320431444， 5 5 T 26C2 (25 24 23 22 2120)(61)9605631275， 6 6 故S T T T 73814144412751905． 35 2 3 6 故a 896，S 1905． …………………………………………………………（17分） 120 35 数学参考答案·第9页（共9页） {#{QQABRQQUggAgQIBAABgCUQFgCgEQkAEACKoOwBAIoAAAyRNABAA=}#}