2024高三诊断-数学答案(1)_2024年4月_01按日期_6号_2024届新结构高考数学合集_新高考19题（九省联考模式）数学合集140套_2024届兰州一诊数学试卷+答案

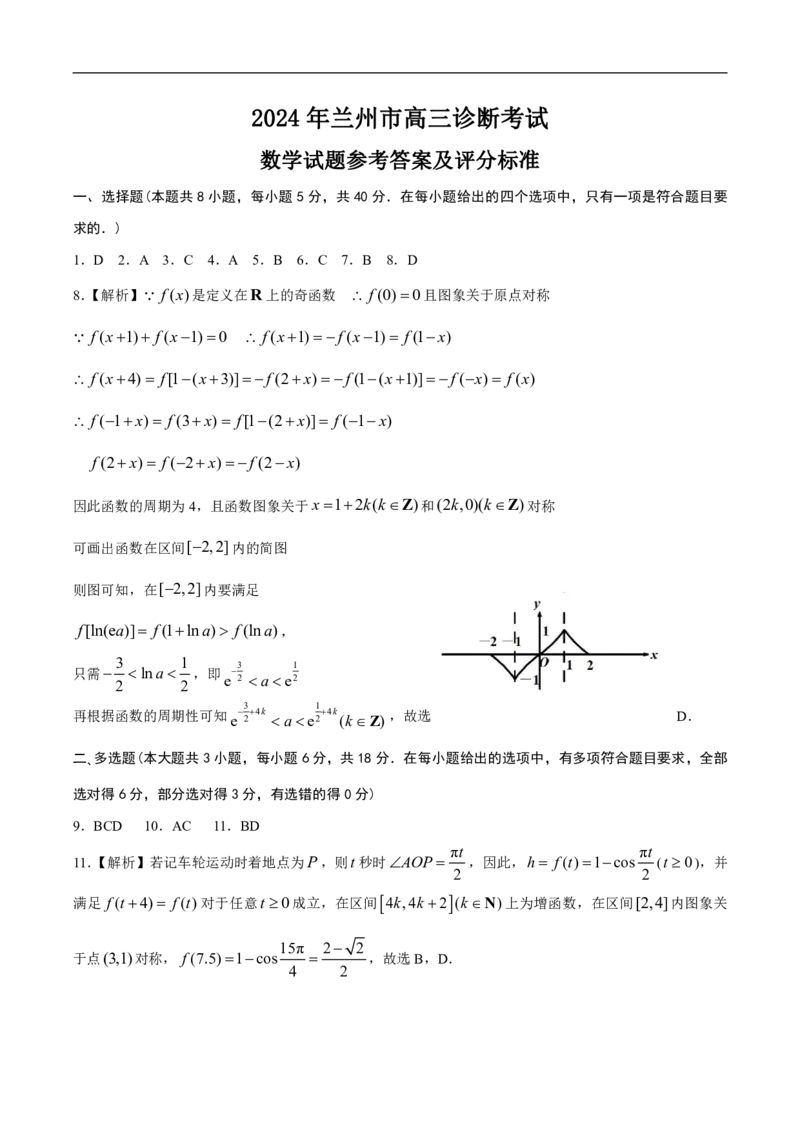
2024 年兰州市高三诊断考试 数学试题参考答案及评分标准 一、选择题(本题共8小题，每小题5分，共40分．在每小题给出的四个选项中，只有一项是符合题目要 求的．) 1．D 2．A 3．C 4．A 5．B 6．C 7．B 8．D 8．【解析】 f(x)是定义在R上的奇函数  f(0)0且图象关于原点对称  f(x1) f(x1)0  f(x1)f(x1) f(1x)  f(x4) f[1(x3)]f(2x)f(1(x1)]f(x) f(x)  f(1x) f(3x) f[1(2x)] f(1x) f(2x) f(2x)f(2x) 因此函数的周期为4，且函数图象关于x12k(kZ)和(2k,0)(kZ)对称 可画出函数在区间[2,2]内的简图 则图可知，在[2,2]内要满足 f[ln(ea)] f(1lna) f(lna)， 3 1 3 1 只需 lna ，即  e 2 ae2 2 2 3 1 再根据函数的周期性可知 e  2 4k ae2 4k (kZ) ，故选 D． 二､多选题(本大题共3小题，每小题6分，共18分．在每小题给出的选项中，有多项符合题目要求，全部 选对得6分，部分选对得3分，有选错的得0分) 9．BCD 10．AC 11．BD πt πt 11．【解析】若记车轮运动时着地点为P，则t秒时AOP ，因此，h f (t)1cos (t 0)，并 2 2 满足 f(t4) f(t)对于任意t 0成立，在区间 4k,4k 2  (kN)上为增函数，在区间[2,4]内图象关 15π 2 2 于点(3,1)对称， f(7.5)1cos  ，故选B，D． 4 2 {#{QQABKYQQogAAABAAAQgCQwX4CAGQkBGAAAoOwBAAoAIBCRFABAA=}#}三､填空题(本大题共3小题，每小题5分，共15分) 1 21 12．y 13． 14．第一空：分别取棱C'D'及CC'的中点M、N，取线段MN上任意一点P e 14 均可(2分)，第二空： 3, 5 (3分)   14．【解析】第一空：因为点P在侧面CDD'C'内（包括边界）且三棱锥PBEF的体积与三棱锥B'BEF的体 积相等，即在侧面CDD'C'内确定一点P，使B'PP平面BEF．又因为E、F分别为棱DD'及CD的中点，故 分别取棱C'D'及CC'的中点M、N，易知B'MPBF，MNPEF，且B'M交MN于点M，BF交EF于点F， 所以平面B'MNP平面BEF，故当点P在线段MN上时，点P到平面BEF的距离与点B'到平面BEF的距离相 等，所以三棱锥PBEF的体积与三棱锥B'BEF的体积相等． 第二空：因为二面角A'ABC的大小为，所以过C作CHAB于H，过H作KHPBB'，则KHC为二面   角A'ABC的平面角，易知B'BC ．当取最大值时，即= 时，此 3 3 时CBAB即底面ABCD 为正方形，在B'C'N中B'C2CN2，B'CN  ，所 K 3  以B'N 3，在B'C'M中B'C2CM2，B'CM ，B'M 5，又因为 2 H MNEF 2，所以B'NM中，B'N 3，MN 2，B'M 5，所以B'NM 为直角三角形，当点P在线段MN上运动时，线段B'P长度的取值范围是  3, 5  ． 四､解答题(本大题共5小题，共77分．解答应写出必要的文字说明､证明过程或演算步骤) n2 3n 15．【解析】 (1)a C2 n3 (nN*)………………5分 n n3 2 a，n1 2，n1 (2)因为数列b 满足：b  1 即b  n n a a ，n2 n n1，n2 n n1 又因为b 2=1+1符合n1当n1时的值，所以数列b的通项公式为b n（1 nN）． 1 n n 1 1 (1 ) 因为2bn ( 1 )n1，所以S = 4 2n  1 (1 1 ) ，2S 1= 1 0．………………13分 2 n 1 2 2n n 2n 1 2 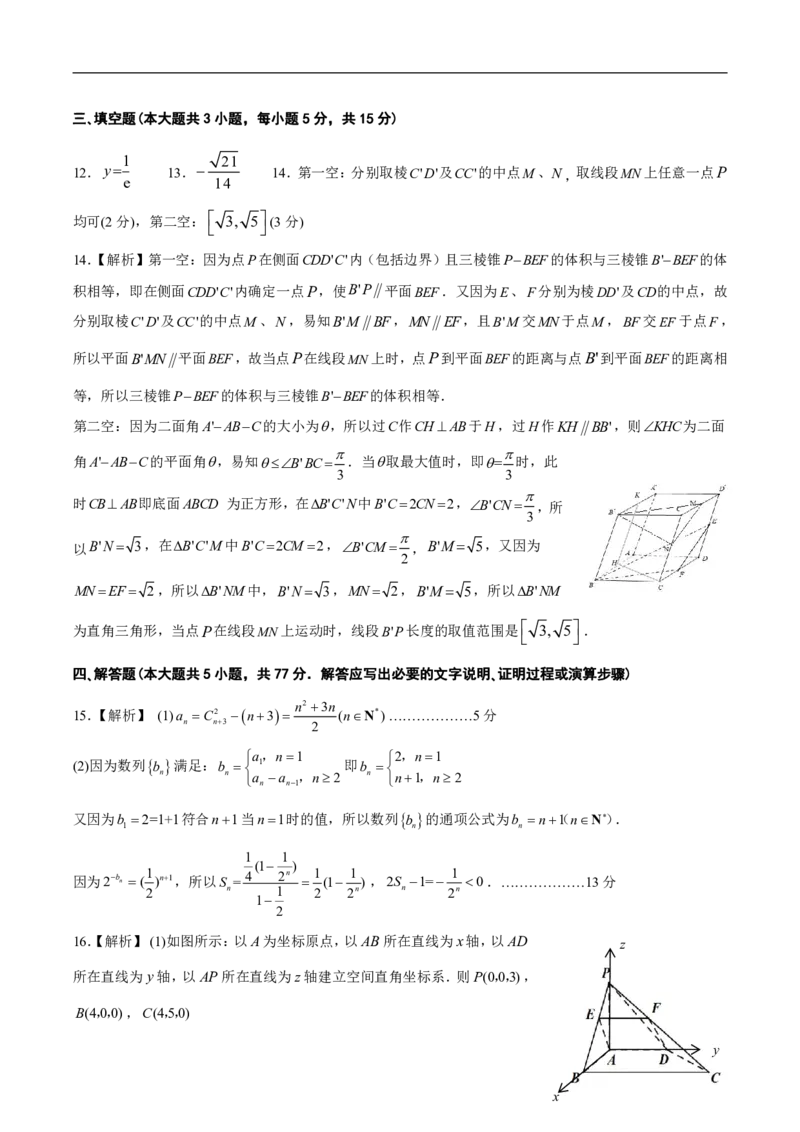16．【解析】(1)如图所示：以A为坐标原点，以AB所在直线为x轴，以AD z 所在直线为y轴，以AP所在直线为z轴建立空间直角坐标系．则P(0，0，3)， B(4，0，0)，C(4，5，0) y x {#{QQABKYQQogAAABAAAQgCQwX4CAGQkBGAAAoOwBAAoAIBCRFABAA=}#}  设E(x，y，z)，由BEBP，可得 x4，y，z 4，0，3 ，     则E(44，0，3)，PB底面AEFD可得PB AE，PB(4，0，3)，AE(44，0，3)，PBAE0解 16 得 ………………6分 25   (1)设平面EAD的法向量为n，AE(44，0，3)，AD(0，3，0) uuur uuur (44)x3z0, 由n AE，n AD，得 令x3得n=3，0，44 ， 3y0, 4 平面ABD的法向量为m，则m=(0，0，1)，二面角EADB的余弦值为 5 44 4 1 则cos m，n   解得 ………………11分 92 16(1)2 5 2 uuur nPC  12 2 PC(4，5，-3)，n=3，0,4若直线PC与平面AEFD所成角为，则sin uuur  n  PC 25 12 2 所以直线PC与平面AEFD所成角的正弦值 ………………15分 25  1 1 3 3 17．【解析】(1)(i)因为X ~B4，  ，所以 P(X 3)C3( )3( ) …………3分 4  4 4 4 64  1 3 1 3 Ck( )k( )4k Ck1( )k1( )5k, (ii)因 为P(X k)Ck( 1 )k( 3 )4k，k 0....4．    4 4 4 4 4 4 解得 1 k  5 4 4 4  Ck( 1 )k( 3 )4k Ck1( 1 )k1( 3 )3k, 4 4  4 4 4 4 4 4 所以k=1时 ，P(X k)最大 …………7分 (2)由题知，BD选项不能同时选择，该同学可以选择单选、双选和三选． 1 1 1 正确答案是两选项的可能情况为AB，AC，AD，BC，CD，每种情况出现的概率均   ； 2 5 10 1 1 1 正确答案是三选项的可能情况为ABC，ACD，每种情况出现的概率为   ； 2 2 4 若该同学做出的决策是单选，则得分的期望如下： 1 1 12 1 1 27 E(A)3 32 3 分，E(B)2 31 3 分， 10 4 5 10 4 20 1 1 12 1 1 27 E(C)3 32 3 分，E(D)2 31 3 分． 10 4 5 10 4 20 若该同学做出的决策是双选，则得分的期望如下： {#{QQABKYQQogAAABAAAQgCQwX4CAGQkBGAAAoOwBAAoAIBCRFABAA=}#}1 1 27 1 1 21 1 1 27 E(AB) 6 3 分，E(AC) 62 3 分，E(AD) 6 3 分， 10 4 20 10 4 10 10 4 20 1 1 27 1 1 27 E(BC) 6 3 分，E(CD) 6 3 分． 10 4 20 10 4 20 若该同学做出的决策是三选，则得分的期望如下： 1 3 1 3 E(ABC) 6 分，E(ACD) 6 分． 4 2 4 2 12 经比较，该同学选择单选A或单选C的得分期望最大，最大值为 分 …………15分 5 18．【解析】(1)圆C过点P4，1，M(2,3)和N(2,1)，因此可以知道圆心在直线y 1上，故可设圆心C(a,1)， 又由于圆C过点P(4,1)，所以a2，r 2，故圆的方程为(x2)2 (y1)2 4， 可得点F(0,1)，因此，抛物线E的方程为x2 4y．…………7分 (2)由条件可知，直线 AB 的斜率必存在，不妨设为 k ，则直线 AB 的方程为： y1k(x4) 即 ykx4k1，  x2 4y 由 得x2 4kx16k40， ykx4k1 其中Δ16k2 64k1616(k2 4k1)0，即k 2 3或k 2 3， 设A(x ,y )，B(x ,y )，过A，B点的抛物线的切线的斜率分别为k ，k ， 1 1 2 2 1 2 x x 则x x 4k，x x 16k4，k  1 ，k  2 ， 1 2 1 2 1 2 2 2 x2 x x x2 过A点的抛物线的切线方程为 y 1  1 (xx )，即 y  1 x 1 ， 4 2 1 2 4 x x2 同理，过B点的抛物线的切线方程为y  2 x 2 2 4  x x2  x x y  1 x 1  x 1 2 2k  2 4  2 由 得 ，即Q(2k,4k1)，  x x2  x x y  2 x 2 y  1 2 4k1  2 4  4 所以点Q在直线 y 2x1上，而点M 也在直线 y 2x1上， 故直线QM 与圆C的另一个交点就是直线 y 2x1与圆C的交点， {#{QQABKYQQogAAABAAAQgCQwX4CAGQkBGAAAoOwBAAoAIBCRFABAA=}#} 2 x (x2)2(y1)2 4   5 x  2 由 得 或 ，  y 2x1  1 y 3 y   5 2 1 故直线QM 与圆C的另一个交点为定点（ ， ） …………17分 5 5 19．【解析】 (1)法一：  3  x2,x0,  2  1 1 d(M,N ) |x|| y2||x|| x2|  x2,0x 4, 则d(M,N )2， 1 2 2 1   3 x2,x4,   2 即d(M,N )的最小值是2 1  23x,x0,  d(M,N ) |x|| y2||x||2x2| 2x,0x 1, 则d(M,N )1， 2 2 y   3x2,x1, Ｍ. 即d(M,N )的最小值为1…………5分 2 x O 法二： N 在直线2xy0上，如图所示d(M，N)的最小值即为 MN ，此时 N 1 1 1 1 M (0，2)，N (0，0)， MN 2，即d(M,N )的最小值是2 1 1 1 y N 在直线 x2y0 上，如图所示 d(M，N ) 的最小值即为 MN ，此时 2 2 2 Ｍ. N 2 M (0，2)，N (1，2)， MN 1，即d(M,N )的最小值为1 2 2 2 x O (2) 解析：法一：当k21时：d(M,N)=x y2， 点（x,y)为直线xk2y2k10(k0)上一动点， 2 1 则当k2 1时 d(M,N)=x x  2  1 2 x  x  2  1 2 2  1 2，即 f(k)=  2 k2 k k2 k2 k2 k k2 k k2 k k2 当k21时， d(M,N)=x x  2  1 2 x x2k12k2  2k22k1， f(k)= 2k2 2k 1 k2 k k2 {#{QQABKYQQogAAABAAAQgCQwX4CAGQkBGAAAoOwBAAoAIBCRFABAA=}#} 1 2   2,k 1, 1 2 所以 f(k)= k2 k 又因为当k 1时  2 5，当0k 1时 2k2 2k1 5 k2 k ，  2k2 2k 1,0k 1,  y 所以 f(k)的最大值为5.…………9分 N Ｍ. 法二：根据(1)直线xk2y2k10(k0)的斜率是 1 ， k2 x 1 O 当 1，即0k 1 时， k2 如图所示d(M，N)的最小值即为 MN ，此时 M(0，2)，N(2k2 2k 1，2)， MN  0(2k22k1) 2k22k1(0k 1) 1 当 1，即k 1时， k2 如图所示d(M，N)的最小值即为 MN ，此时 y 1 2 1 2 1 2 Ｍ. M(0，2)，N(0，  )， MN  2(  )   2(k 1) k2 k k2 k k2 k x 2k2 2k 1,0k 1, O  所以 f(k)= 1 2 所以 f(k)的最大值为5   2,k 1, N k2 k (3)法一：令xek，则kek  xlnx，0 xe d(M，N)|ekm||kekn|max{|xxlnxmn|,|xxlnxmn|}(max{a,b}表示a、b中的较大者) 令g(x) xxlnx(0 xe) ，则g(x)2lnx 0在区间(e2,e]内成立，g(x)在区间(e2,e]内为增 1 函数，因此  g(e2) g(x) g(e) 2e ， e2 令h(x) xxlnx(0 xe)，则h(x)lnx0在区间(1,e]内成立，h(x)在区间(1,e]内为减函数， 因此0h(e)h(x) g(1)1， 1 所以 f(m，n) max{| mn|,|2emn|,|mn|,|1mn|} e2 1 |2e( )| e2 |10| 1 所以 f(m,n)max{ , }e ， 2 2 2e2 1 1 1 当m+n=e 且  ne 时，取最小值．…………17分 2e2 2e2 2 {#{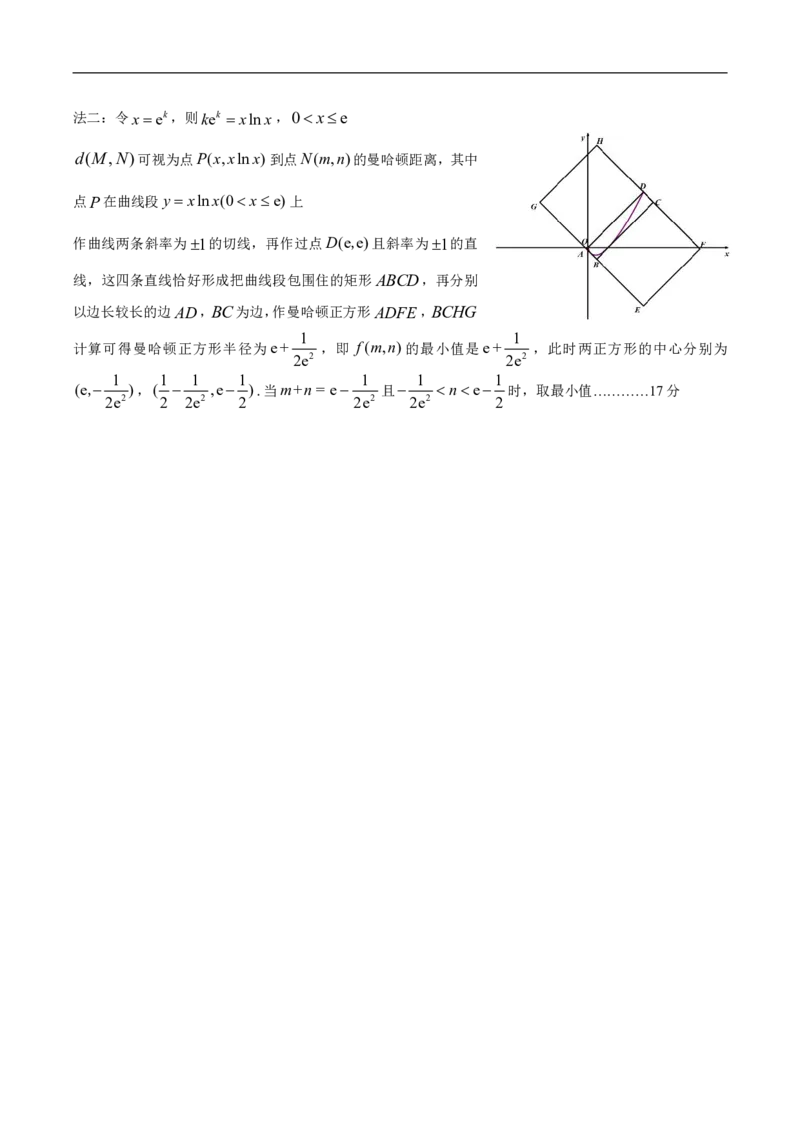QQABKYQQogAAABAAAQgCQwX4CAGQkBGAAAoOwBAAoAIBCRFABAA=}#}法二：令xek，则kek  xlnx，0 xe d(M,N)可视为点P(x,xlnx)到点N(m,n)的曼哈顿距离，其中 点P在曲线段 y  xlnx(0 xe)上 作曲线两条斜率为1的切线，再作过点D(e,e)且斜率为1的直 线，这四条直线恰好形成把曲线段包围住的矩形ABCD，再分别 以边长较长的边AD，BC为边，作曼哈顿正方形ADFE，BCHG 1 1 计算可得曼哈顿正方形半径为e+ ，即 f(m,n)的最小值是e+ ，此时两正方形的中心分别为 2e2 2e2 1 1 1 1 1 1 1 (e, )，(  ,e ).当m+n = e 且  ne 时，取最小值…………17分 2e2 2 2e2 2 2e2 2e2 2 {#{QQABKYQQogAAABAAAQgCQwX4CAGQkBGAAAoOwBAAoAIBCRFABAA=}#}