辽宁省鞍山市重点高中协作校2025届高三上学期期中考试数学答案(1)_12月_241201辽宁省鞍山市重点高中协作校2025届高三上学期期中考试

2024年期中考试 高三数学试题 (A) 参考答案 一．选择题：本题共8小题，每小题5分，共40分。在每小题给出的四个选项中，只有一项是符合题目 要求的。 二．选择题：本题共3小题，每小题6分，共18分。在每小题给出的选项中，有多项符合题目要求。全 部选对的得6分，部分选对的得3分，有选错的得0分。 题号 1 2 3 4 5 6 7 8 9 10 11 答案 C A B D B C D A BC CD BD 三．填空题：本大题共3小题，每小题5分，共15分。 12.6 ; 13. 14.5x-y+2=0 ； 四．解答题：本题共5小题，共77分。解答应写出文字说明、证明过程或演算步骤。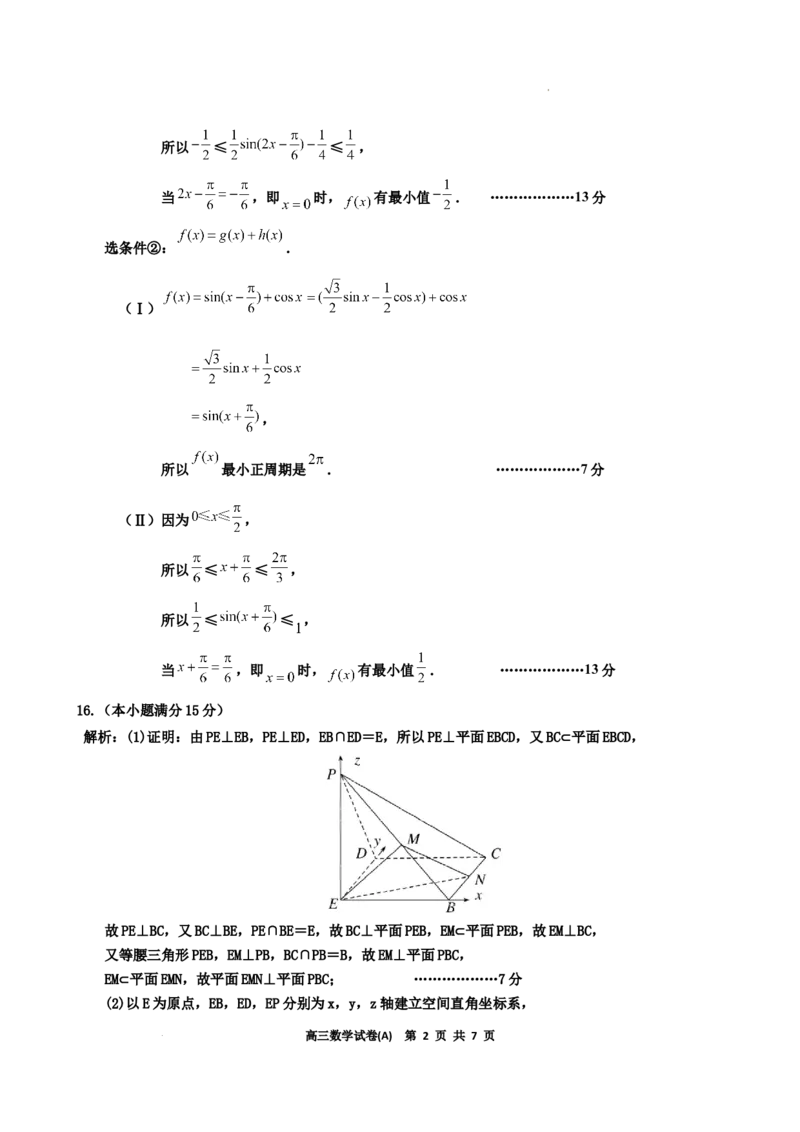 15.（本小题满分13分）注：如果选择条件①和条件②分别解答，按第一个解答计分． 解：选条件①： ； （Ⅰ） ， 所以 的最小正周期是 ． ………………7分 （Ⅱ）因为 ， 所以 ≤ ≤ ， 所以 ≤ ≤ ， 高三数学试卷(A) 第 1 页 共 7 页 学科网（北京）股份有限公司所以 ≤ ≤ ， 当 ，即 时， 有最小值 ． ………………13分 选条件②： ． （Ⅰ） ， 所以 最小正周期是 ． ………………7分 （Ⅱ）因为 ， 所以 ≤ ≤ ， 所以 ≤ ≤ ， 当 ，即 时， 有最小值 ． ………………13分 16.（本小题满分15分） 解析：(1)证明：由PE⊥EB，PE⊥ED，EB∩ED＝E，所以PE⊥平面EBCD，又BC⊂平面EBCD， 故PE⊥BC，又BC⊥BE，PE∩BE＝E，故BC⊥平面PEB，EM⊂平面PEB，故EM⊥BC， 又等腰三角形PEB，EM⊥PB，BC∩PB＝B，故EM⊥平面PBC， EM⊂平面EMN，故平面EMN⊥平面PBC； ………………7分 (2)以E为原点，EB，ED，EP分别为x，y，z轴建立空间直角坐标系， 高三数学试卷(A) 第 2 页 共 7 页 学科网（北京）股份有限公司设PE＝EB＝2，设N(2，m,0)，B(2,0,0)，D(0,2,0)，P(0,0,2)，C(2,2,0)，M(1,0,1)， EM＝(1,0,1)，EB＝(2,0,0)，EN＝(2，m,0)， 设平面EMN的法向量为 ＝(x，y，z)， 由，得 ＝(m，－2，－m)， 平面BEN的法向量为 ＝(0,0,1)， 故|cos〈 ， 〉|＝＝，得m＝1， 故存在N为BC的中点． ………………15分 17.（本小题满分15分） 解析：（1）由已知及正弦定理得 又 由，可得 又 ………………6分 （2） 的面积 ． 由已知及余弦定理得 又 ，故 ， 当且仅当 时，等号成立． 因此 的面积的最大值为 ………………15分 18.（本小题满分17分） 解：（Ⅰ） 因为 ， 所以曲线 在点 处的切线方程为 . ………...….….…...5分 （Ⅱ）由（Ⅰ）知： ，（ ） 因为 ，令 ，所以 或 ， 高三数学试卷(A) 第 3 页 共 7 页 学科网（北京）股份有限公司当 时， ， 则 的变化情况如下表： 极大值 极小值 当 时， ，则 恒成立， 在 内恒增； 当 时， ，则 的变化情况如下表： 极大值 极小值 综上，当 时，单调递增区间是 和 ，单调递减区间是 ； 当 时，单调递增区间是 ，无单调递减区间； 当 时，单调递增区间是 和 ，单调递减是 . ………...….…………...….…11分 （Ⅲ）当 时，令 ，得 或 ，易知 则 的变化情况如下表： 极小值 极大值 所以当 时， 取得极小值 高三数学试卷(A) 第 4 页 共 7 页 学科网（北京）股份有限公司由于 ，则 ， ， ， 所以由极小值定义及 的单调性可知：当 时， . 接下来，研究 在 的变化情况. 因为 恒成立，设 对称轴 ， ， 所以由二次函数的性质可知：当 时， 恒成立 所以 在 时恒成立. 综上所述：当 时， . ………...….…………...….…...17分 19.（本小题满分17分） （Ⅰ） （或 ） ………...….…………...….…...5分 （Ⅱ）必要性：因为 数列 是递减数列， a −a =−1 (k=1,2,⋯2023) 所以 k+1 k ， 所以 是首项为 ，公差为 的等差数列， a =2024+(2023−1)×(−1)=2 所以 2023 ………...….…………...….…...…8分 a −a ≥−1 a −a ≥−1 a a  1 充分性：由于 2024 2023 ， 2023 2022 ，…， 2 1 a −a ≥−2020 a ≥a −2022=2 所以 2024 1 ， 即 2024 1 ， a =2 a a 10 (k=1,2,⋯2021) 因为 2023 ，所以 k1 k ， ， 所以数列 是递减数列. 综上，结论得证． . .…...….……………...…11分 高三数学试卷(A) 第 5 页 共 7 页 学科网（北京）股份有限公司c =a −a (k=1,2,⋯n−1) （Ⅲ）令 k k+1 k ， c =±1 则 k ． a =a +c 因为 2 1 1， a =a +c +c 3 1 1 2，  a =a +c +c +⋯c n 1 1 2 n−1， S(A )=na+(n−1)c +(n−2)c +(n−3)c +⋯+c 所以 n 1 1 2 3 n−1 =(n−1)+(n−2)+⋯+1−(1−c )(n−1)−(1−c )(n−2)−⋯−(1−c ) 1 2 n−1 n(n−1) = −[(1−c )(n−1)+(1−c )(n−2）+⋯+(1−c )] 2 1 2 n−1 c =±1 1−c (k=1,2,⋯n−1) 因为 k ，所以 k为偶数 ， （1−c )(n−1)+(1−c )(n−2)+⋯+(1−c ) 所以 1 2 n−1 为偶数． n(n−1) 2 n(n−1) 所以要使 ，必须使 为偶数，即 整除 ， 亦即 n=4m 或 n=4m+1 ． 当 n=4m 时， a =a =0 a =−1 a =1 (k=1,2,⋯m) 数列 的项满足 4k−1 4k−3 ， 4k−2 ， 4k 时， a =0 有 1 ， ； 当 n=4m+1 时， a =a =0 a =−1 a =1 a =0(k=1,2,⋯m) 数列 的项满足 4k−1 4k−3 ， 4k−2 ， 4k ， 4k+1 时， 高三数学试卷(A) 第 6 页 共 7 页 学科网（北京）股份有限公司a =0 有 1 ， ． 当 n=4m+2 ， n=4m+3 时， n(n−1) 不能被 整除， a =0 此时不存在 数列 使得 1 ， ． . .…...….…………...17分 高三数学试卷(A) 第 7 页 共 7 页 学科网（北京）股份有限公司