320文数答案_2024年3月_013月合集_2024届内蒙古赤峰市高三下学期3·20模拟考试_内蒙古赤峰市2024届高三下学期3.20模拟考试文科数学试题

赤峰市高三年级 3.20 模拟考试试题 文科数学答案 2024.03 一、选择题：本大题共 12 小题，每小题 5 分，满分 60 分．在每小题给出的四 个选项中，只有一项是符合题目要求的． 题号 1 2 3 4 5 6 7 8 9 10 11 12 答案 C B A C B D A D B B C D 二、填空题：  13、48 14、 14 15、 f(x)=sin(2x+ ) 16、①③④ 6 三、解答题： 17、解：（1）选①，当n=1时，a =2a −2，即a =2 ...............................................1分 1 1 1 当n2时，S =2a −2 ① n n S =2a −2②..........................................................2分 n−1 n−1 ①-②得：a =2a −2a ，..................................................................................................3分 n n n−1 a 即 n =2 ..................................................................................................................................4分 a n−1   所以数列 a 是以2为首项，2为公比的等比数列................................................................5分 n 所以a =2n ................................................................................................................................6分 n 选②，当n=1时，a =S =2，即a =2...........................................................................1分 1 1 1 n(n+1） S 2 2 当n2时，a = n = ...............................................................................................2分 n S n(n−1) n−1 2 2 n(n+1) n(n−1) 即 a =2 2 − 2 =2n..........................................................................................................3分 n 当n=1时，a =2符合上式....................................................................................................4分 1   所以数列 a 是以2为首项，2为公比的等比数列................................................................5分 n 所以a =2n ................................................................................................................................6分 n 1 {#{QQABCYSAogAgABIAAAhCQwEoCAKQkAECACoGRFAMsAIAyRFABCA=}#}因为b =log a ，所以b =n，............................................................................................7分 n 2 n n 1 1 所以 = ...............................................................................................................8分 b b n(n+1) n n+1 1 1 1 1 所以 = = − ...........................................................................................9分 b b n(n+1) n n+1 n n+1  1 1 1 1 1  所以 T =  1−  +  −  ++  − ...............................................................10分 n  2 2 3 n n+1 1 =1− ...........................................................................................................................11分 n+1 因为nN 所以T 1.......................................................................................................12分 n 18、解（1）由甲商场分数的频率分布直方图，得对甲商场评分低于30分的频率为： (0.003+0.005+0.012)10=0.2，......................................................................................2分 ∴对甲商场评分低于30的人数为1000.2=20人，...............................................................3分 （2）对乙商场评分在[0，10)范内的有2人，设为m、n，................................................4分 对乙商场评分在[10，20)范围内的有3人，设为a、b、c，...............................................5分 从这5人中随机选出2人的选法为： mn、ma、mb、mc、na、nb、nc、ab、ac、bc，共10种，.............................7分 其中2人评分都在  10，20 ) 范围内的选法包括：ab、ac、bc，共3种，.......................8分 3 故2人评分都在  10，20 ) 范围内的概率为P = ，...............................................................9分 10 （3）选择乙商场，理由如下： （i）：从两个商场得分低于30分的人数所占的比例来看，由（1）得，抽样的100人中， 甲商场评分低于30的人数为20， ∴甲商场评分低于30分的人数所占的比例为20%，..........................................................10分 乙商场评分低于30分的人数为2+3+5=10， ∴乙商场得分低于30分的人数所占的比例为10%，..........................................................11分 ∴会选择乙商场消费................................................................................................................12分 （ii）： x =10（50.003+150.005+250.012+350.020+450.020+550.040） 甲 2 {#{QQABCYSAogAgABIAAAhCQwEoCAKQkAECACoGRFAMsAIAyRFABCA=}#}=41.9.....................................................................................................................................10分 1 x = （52+153+255+3515+4540+5535）=44.3..........................11分 乙 100 x  x ∴会选择乙商场消费。.........................................................................................12分 甲 乙 以上给出了2种理由，考生答出其中任意一种或其他合理理由均可得分。 ex ex(x−1) 19、解（1）：当a=1时， f (x)= ，则 f(x)= ，..............................................1分 x x2 所以，f (1)=e，f(1)=0，.....................................................................................................2分 故当a=1时，曲线y= f (x)在点 (1, f (1)) 处的切线方程为y−e=0，即y=e....................3分 （2）当a=2时， f (x)=   1 +1  ex = (x+1)ex ，该函数的定义域为 x x0 ， x  x (x+2)xex−(x+1)ex ( x2+x−1 ) ex f(x)= = ，........................................................................4分 x2 x2 1+ 5 5−1 由 f x 0，即x2+x−10，解得x− 或x ，...........................................5分 2 2  1+ 5  5−1  因此，当a=2时，函数 f (x)的单调递增区间为−,− 、 ,+....................6分   2     2   （3）法I ：因为f (x)=   1 +a−1  ex，则f(x)=   1 +a−1− 1  ex= ((a−1)x2+x−1 ) ex ，............7分 x  x x2 x2 令g(x)=(a−1)x2+x−1，因为函数 f (x)在(0,1)上有且只有一个极值点， 则函数g(x)在(0,1)上有一个异号零点，.................................................................................8分 当a=1时，对任意的x(0,1)，g(x)=x−10恒成立，无零点，故不符合题意；..........9分 当a1时，函数g(x)=(a−1)x2+x−1在(0,1)上单调递增， 因为g(0)=−10，只需g(1)=a−10，故a1符合题意；................................................10分 1 当a1时，函数g(x)的图象开口向下，对称轴为直线x=− 0， 2(a−1) 因为g(0)=−10，只需g(1)=a−10，故a1不符合题意，舍去....................................11分 综上所述，实数a的取值范围是(1,+) ..................................................................................12分 3 {#{QQABCYSAogAgABIAAAhCQwEoCAKQkAECACoGRFAMsAIAyRFABCA=}#}法II：令 (a−1)x2 +x−1=0.................................................................................................7分 1 1 则(a−1)= − 有根...........................................................................................................8分 x2 x 1 令t = (1，+) ......................................................................................................................9分 x 设g(t)=t2 −t .........................................................................................................................10分 由题意可知a−10................................................................................................................11分 ∴a1......................................................................................................................................12分 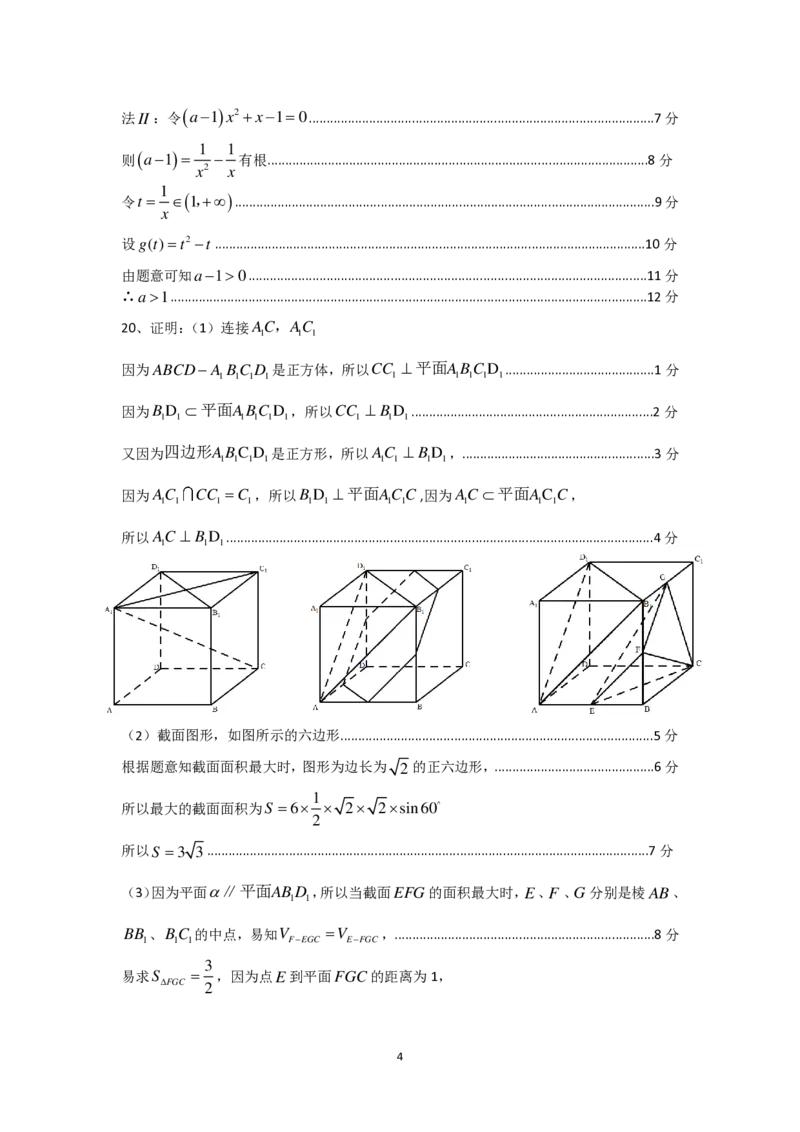20、证明：（1）连接AC，AC 1 1 1 因为ABCD−A BC D 是正方体，所以CC ⊥平面ABCD ..........................................1分 1 1 1 1 1 1 1 1 1 因为BD 平面ABCD ，所以CC ⊥ BD ....................................................................2分 1 1 1 1 1 1 1 1 1 又因为四边形ABC D 是正方形，所以AC ⊥ BD ，......................................................3分 1 1 1 1 1 1 1 1 因为AC CC =C ，所以BD ⊥平面ACC ,因为AC 平面ACC， 1 1 1 1 1 1 1 1 1 1 1 所以AC ⊥ BD ........................................................................................................................4分 1 1 1 （2）截面图形，如图所示的六边形........................................................................................5分 根据题意知截面面积最大时，图形为边长为 2的正六边形，.............................................6分 1 所以最大的截面面积为S =6  2 2sin60 2 所以S =3 3............................................................................................................................7分 （3）因为平面∥平面ABD ，所以当截面EFG的面积最大时，E、F 、G分别是棱AB、 1 1 BB 、BC 的中点，易知V =V ，.........................................................................8分 1 1 1 F−EGC E−FGC 3 易求S = ，因为点E到平面FGC的距离为1， FGC 2 4 {#{QQABCYSAogAgABIAAAhCQwEoCAKQkAECACoGRFAMsAIAyRFABCA=}#}1 3 1 所以V =V =  1= ......................................................................................9分 F−EGC E−FGC 3 2 2 易求EC = 5,GC = 5,EG= 6 , 1 14 21 所以S =  6 = .......................................................................................10分 EGC 2 2 2 设F 到平面EGC的距离为d 1 1 21 1 21 所以 S d =  d = ，所以d = .......................................................11分 3 EGC 3 2 2 7 21 所以F 到平面EGC的距离为 ......................................................................................12分 7  p 21、解析：（1）由题可知，42 =2p  5− ........................................................................2分  2 解得， p=2或 p =8（舍）...............................................................................................3分 所以，抛物线P的方程为 y2 =4x.................................................................................4分 （2）设直线AB方程为x=my+1,且A(x,y )，B(x ,y ), ..................................................5分 1 1 2 2 x=my+1 联立 ，可得y2−4my−4=0 ................................................................................6分 y2 =4x 则 ..........................................................................................................7分 y +y =4m,y y =−4, 1 2 1 2 则 AB = 1+m2 (y +y )2−4y y ........................................................................................8分 1 2 1 2 = 1+m2 16+16m2 =4m2 +4............................................................................................9分 4 同理CD =4+ ，...............................................................................................................10分 m2 4 4 所以 AB + CD =4m2+ +82 4m2 +8=16，当且仅当m=1时取等号............11分 m2 m2 所以 AB + CD 的最小值为16.................................................................................................12分 2p [注]：本题如果直接使用过焦点的弦长公式 AB = 解答，本问分数减半；如果有此 sin2 公式的推导过程，本问给满分。  x=cos x=cos 22、解：（1）由 ，可得 ..........................................................1分 y=4+sin y−4=sin 5 {#{QQABCYSAogAgABIAAAhCQwEoCAKQkAECACoGRFAMsAIAyRFABCA=}#}消去参数得x2 +(y−4)2 =sin2+cos2=1，..........................................................2分 所以曲线C 的普通方程为x2+(y−4)2 =1，又因为2...........................................3分 2 所以曲线C 的普通方程为x2+(y−4)2 =1（3 y4）.........................................................4分 2  x=2cos （3）因为曲线C 的参数方程为 (为参数）， 1 y= 3sin 所以设点M 的坐标为(2cos, 3sin)，..............................................................................5分 设圆心C 与C 上任意一点的距离为d 2 1 则d = 4cos2+(4− 3sin)2 ................................................................................................6分 = −sin2−8 3sin+20.......................................................................................................7分 设sin=t,t−1,1，则d = −t2 −8 3t+20..............................................................8分 = 19−2 48 ..............................................................9 分 d =4− 3， 所以 MN =d−r=3− 3.................................................................10分 min min 23、解：①当m=2时， f(x)4− x+1，即 x−2 + x+14.......................................1分 3 3 当x−1时，不等式化为−x+2−x−14，解得x− ，所以x− .......................2分 2 2 当−1x2时，不等式化为−x+2+x+14，解得x............................................3分 5 5 当x2时，不等式化为x−2+x+14，解得x ，所以x ...............................4分 2 2  3 5  综上，原不等式的解集为 −,−   ,+..................................................................5分  2 2  ②若 f(x)2m− x+1恒成立，即  x−m + x+1  2m................................................6分 min 因为 x−m + x+1 x−m−x−1= m+1(当且仅当(x−m)(x+1)0时，等号成立)..7分 所以 m+12m，即m+12m或m+1−2m，..................................................................8分 1 解得m1或m− ..................................................................................................................9分 3 故m的取值范围为(−,1 ...................................................................................................10分 6 {#{QQABCYSAogAgABIAAAhCQwEoCAKQkAECACoGRFAMsAIAyRFABCA=}#}