文档内容
2023~2024 学年度下学期六校高二期末联考试卷
数 学
考生注意:
1.本试卷分选择题和非选择题两部分.满分150分,考试时间120分钟.
2.答题前,考生务必用直径0.5毫米黑色墨水签字笔将密封线内项目填写清楚.
3.考生作答时,请将答案答在答题卡上.选择题每小题选出答案后,用2B铅笔把答题卡上
对应题目的答案标号涂黑;非选择题请用直径0.5毫米黑色墨水签字笔在答题卡上各题的答
题区域内作答,超出答题区域书写的答案无效,在试题卷、草稿纸上作答无效.
4.本卷命题范围:人教A版选择性必修第二册第五章,选择性必修第三册.
一、选择题:本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项
是符合题目要求的.
1. 若 ,则 ( )
.
A 2 B. 6 C. 2或6 D. 2或507
2. 设某制造公司进行技术升级后的第x个月( )的利润为y(单位:百万元),根据统计数
据,求得y关于x的经验回归方程为 ,若 时的观测值 ,则 时的残差为(
)
A. B. 1 C. 3 D. 6
3. 若定义在 上的函数 有 ,则 的单调递减区间是(
)
A. B. C. D.
4. 李白的一句“烟花三月下扬州”让很多人对扬州充满向往.据统计,唐朝约有120名诗人写下了400多首
与扬州有关的诗篇,某扬州短视频博主从中选取了7首,制作了分别赏析这7首诗的7个短视频(含甲、
乙),准备在某周的周一到周日发布,每天只发布 1个,每个短视频只在其中1天发布,若甲、乙相邻两
天发布,则这7个短视频不同的发布种数为( )
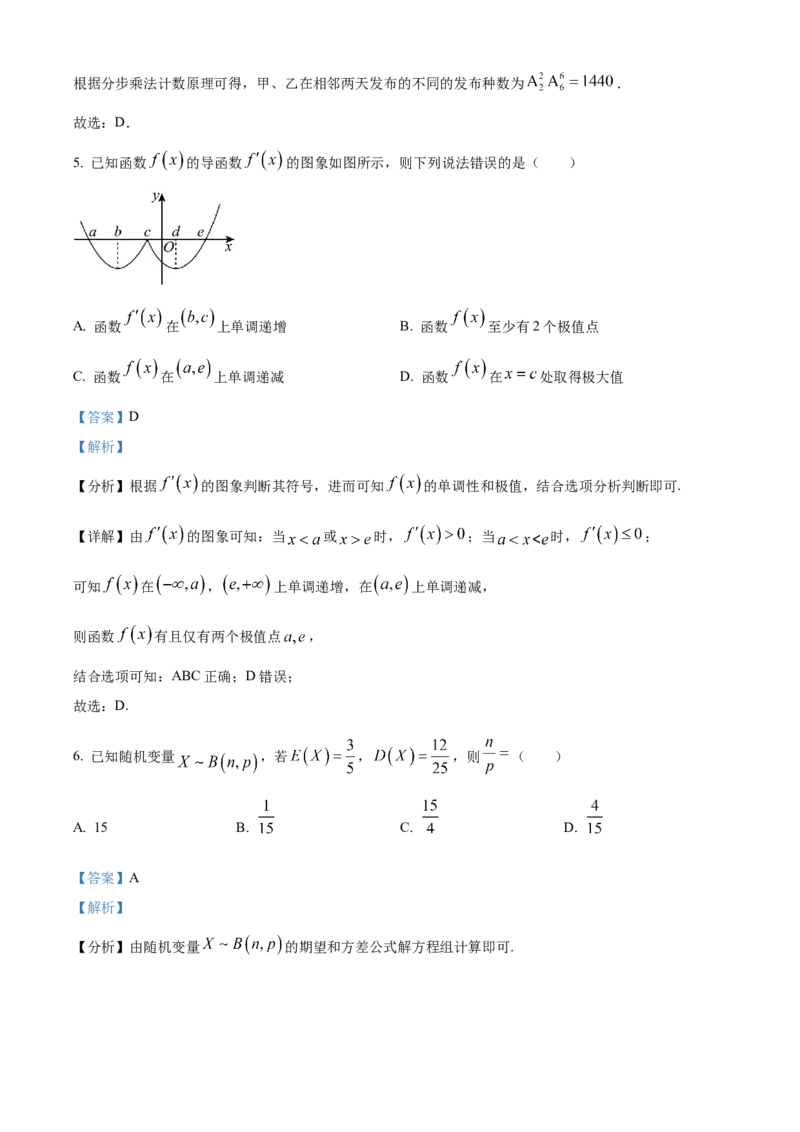
A. 180 B. 360 C. 720 D. 14405. 已知函数 的导函数 的图象如图所示,则下列说法错误的是( )
A. 函数 在 上单调递增 B. 函数 至少有2个极值点
C. 函数 在 上单调递减 D. 函数 在 处取得极大值
6. 已知随机变量 ,若 , ,则 ( )
A. 15 B. C. D.
7. 已知函数 有3个不同的零点,则 的取值范围是( )
A. B. C. D.
8. 小明在某不透明的盒子中放入4红4黑八个球,随机摇晃后,小明从中取出一个小球丢掉(未看被丢掉
小球的颜色).现从剩下7个小球中取出两个小球,结果都是红球,则丢掉的小球也是红球的概率为(
)
A. B. C. D.
二、选择题:本题共3小题,每小题6分,共18分.在每小题给出的选项中,有多项符合题
目要求.全部选对的得6分,部分选对的得部分分,有选错的得0分.
9. 若 的展开式中第4项与第9项的二项式系数相等,则展开式中系数最大的项为( )
.
A 第4项 B. 第5项 C. 第6项 D. 第7项
10. 甲、乙、丙、丁4人每人随机选取VisualBasie、VisualC++,VisualFoxpro三种编程语言之一进行学
习,每种编程语言至少有1人学习,A表示事件“甲学习VisualBasic编程语言”;B表示事件“乙学习
VisualBasic编程语言”;C表示事件“乙学习VisualC++编程语言”,则( )A. 事件A与B相互独立 B. 事件A与C不是互斥事件
C. D.
11. 已知定义域为 的函数 的导函数为 ,若函数 和 均为偶函数,且
,则( )
A. B. C. D.
三、填空题:本题共3小题,每小题5分,共15分.
12. 已知随机变量 的分布列 ,则 ______.
13. 已知 是函数 的两个极值点,若 ,且 的极小值为整
数,则 ______.
14. 五一小长假,多地迎来旅游高峰期,各大旅游景点都推出了种种新奇活动以吸引游客,小明去某景点
游玩时,发现了一个趣味游戏,游戏规则为:一个会走路 的机器人从一数轴上的原点出发沿该数轴行走,
游客可以设定机器人总共行走的步数n,机器人每一步会随机选择前或向后行走,且每一步的距离均为一
个单位,设机器人走完设定的n步后所在位置对应数为随机变量 ,则 __________,
__________.
四、解答题:本题共5小题,共77分.解答应写出文字说明、证明过程或演算步骤.
15. 已知 .
的
(1)若 ,求 值;
(2)若 ,求m的值.
16. 已知函数 .(1)求 在点 处的切线方程;
(2)求函数 的极值.
17. 光明高级中学高三年级理科考生800人都参加了本学期的期中调研测试,学校把本次测试数学成绩达
到120分以上(包含120分)的同学的数学成绩等第定为优秀,物理成绩达到90分以上(包含90分)的
同学的物理成绩等第定为优秀.现从理科考生中随机抽取10名同学调研本次测试的数学和物理成绩,如下
表:
8
数学(分) 119 145 99 95 135 120 122 130 120
5
8
物理(分) 84 90 82 84 83 81 83 90 82
1
(1)试列出 列联表,并依据 的独立性检验分析能否认为本次测试理科考生的数学成绩的等
第优秀与物理成绩的等第是否优秀有关?
(2)如果本次测试理科考生的物理成绩 ,用样本估计总体,以10名同学物理成绩的平均
数为 ,方差为 ,若从参加考试的800名理科考生中随机抽取4人,求这4人中至少有1人的物理成绩
的等第优秀的概率.
参考数据:取 , , , .若 ,则
, ,
.
, .
.
0.10 0.05 0.025 0010 0.005
2.706 3.841 5.024 6.635 7.879
18. 2024年4月25日—4月29日,“与辉同行”开启了一场深入中原的文化之旅,让河南文旅打开了流量密码.某景区趁此时机,举行五一游该景区网上购票抽奖活动,在网上购买该景区门票的游客,可通过手机
扫景区提供的二维码进入抽奖活动页面,每张门票可从6个减免红包中随机抽取2个,6个红包的金额分
别为5元、5元、10元、10元、30元、60元,已知该景区门票每张120元,全部实行网上购票.
(1)记购买1张门票的游客通过抽奖获得的红包金额之和为X,求X的分布列与期望;
(2)已知每位游客除门票外平均在该景区消费30元、40元、60元的概率分别为 , , ,举行此抽
奖活动后预计可使该景区五一期间客流量增加40%,假设每位购票游客都进行了抽奖,回答下列问题并说
明理由:
①举行抽奖活动后该景区在五一期间的门票收入是增加了,还是减少了?
②举行抽奖活动后该景区在五一期间的总收入是增加了,还是减少了?
19. 定义:若函数 与 的图象在 上有且仅有一个交点,则称函数 与 在 上
单交,此交点被称为“单交点”.已知函数 , , .
(1)讨论函数 的单调性;
(2)当 时,
(i)求证:函数 与 在 上存在“单交点” ;
(ⅱ)对于(i)中的正数 ,证明: .2023~2024 学年度下学期六校高二期末联考试卷
数学
考生注意:
1.本试卷分选择题和非选择题两部分.满分150分,考试时间120分钟.
2.答题前,考生务必用直径0.5毫米黑色墨水签字笔将密封线内项目填写清楚.
3.考生作答时,请将答案答在答题卡上.选择题每小题选出答案后,用2B铅笔把答题卡上
对应题目的答案标号涂黑;非选择题请用直径0.5毫米黑色墨水签字笔在答题卡上各题的答
题区域内作答,超出答题区域书写的答案无效,在试题卷、草稿纸上作答无效.
4.本卷命题范围:人教A版选择性必修第二册第五章,选择性必修第三册.
一、选择题:本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项
是符合题目要求的.
1. 若 ,则 ( )
A. 2 B. 6 C. 2或6 D. 2或507
【答案】D
【解析】
【分析】通过组合数的性质即可得到答案.
【详解】由题意知 或 所以 或
故选:D.
2. 设某制造公司进行技术升级后的第x个月( )的利润为y(单位:百万元),根据统计数
据,求得y关于x的经验回归方程为 ,若 时的观测值 ,则 时的残差为(
)
A. B. 1 C. 3 D. 6
【答案】B
【解析】
【分析】利用残差的定义求解.
【详解】解:因为 时的预测值为 ,所以残差为 .
故选:B.
3. 若定义在 上的函数 有 ,则 的单调递减区间是(
)
A. B. C. D.
【答案】C
【解析】
【分析】由导函数定义可得 ,再利用导函数求单调减区间即可.
【详解】 ,
, ,
由 ,解得 ,
故 的单调递减区间是 .
故选:C.
4. 李白的一句“烟花三月下扬州”让很多人对扬州充满向往.据统计,唐朝约有120名诗人写下了400多首
与扬州有关的诗篇,某扬州短视频博主从中选取了7首,制作了分别赏析这7首诗的7个短视频(含甲、
乙),准备在某周的周一到周日发布,每天只发布 1个,每个短视频只在其中1天发布,若甲、乙相邻两
天发布,则这7个短视频不同的发布种数为( )
A. 180 B. 360 C. 720 D. 1440
【答案】D
【解析】
【分析】元素相邻的排列问题,利用捆绑法解决即可.
【详解】先将甲、乙排为一列,有 种方法,
再将其视为一个整体与其余5个视频排成一列,有 种方法,根据分步乘法计数原理可得,甲、乙在相邻两天发布的不同的发布种数为 .
故选:D.
5. 已知函数 的导函数 的图象如图所示,则下列说法错误的是( )
A. 函数 在 上单调递增 B. 函数 至少有2个极值点
C. 函数 在 上单调递减 D. 函数 在 处取得极大值
【答案】D
【解析】
【分析】根据 的图象判断其符号,进而可知 的单调性和极值,结合选项分析判断即可.
【详解】由 的图象可知:当 或 时, ;当 时, ;
可知 在 , 上单调递增,在 上单调递减,
则函数 有且仅有两个极值点 ,
结合选项可知:ABC正确;D错误;
故选:D.
6. 已知随机变量 ,若 , ,则 ( )
A. 15 B. C. D.
【答案】A
【解析】
【分析】由随机变量 的期望和方差公式解方程组计算即可.【详解】因为 , ,
所以 ,
即 ,所以 ,
所以 .
故选:A.
7. 已知函数 有3个不同的零点,则 的取值范围是( )
A. B. C. D.
【答案】D
【解析】
【分析】求得 ,得出函数 的单调性与极值,结合 有3个不同的零点,列出不
等式,即可求解.
【详解】由函数 ,可得 ,
令 ,解得 或 ,
令 ,解得 或 ;令 ,解得 ,
则 在 和 上单调递增,在 上单调递减,
又由 , ,
要使 有3个不同的零点,则 ,解得 ,所以实数 的取值范围是 .
故选:D.
8. 小明在某不透明的盒子中放入4红4黑八个球,随机摇晃后,小明从中取出一个小球丢掉(未看被丢掉
小球的颜色).现从剩下7个小球中取出两个小球,结果都是红球,则丢掉的小球也是红球的概率为(
)
A. B. C. D.
【答案】B
【解析】
【分析】先由古典概率公式求出 ,再由全概率公式求出
,最后由条件概率求出 即可.
【详解】用 表示丢掉一个小球后任取两个小球均为红球,用 表示丢掉的小球为红球, 表示丢掉的
小球为黑球,
则 , ,
由全概率公式可得
,
所以 ,
故选:B.
【点睛】关键点点睛:条件概率公式为 ,全概率公式为.
二、选择题:本题共3小题,每小题6分,共18分.在每小题给出的选项中,有多项符合题
目要求.全部选对的得6分,部分选对的得部分分,有选错的得0分.
9. 若 的展开式中第4项与第9项的二项式系数相等,则展开式中系数最大的项为( )
A. 第4项 B. 第5项 C. 第6项 D. 第7项
【答案】CD
【解析】
【分析】根据二项式系数的性质即可求解.
【详解】因为 的展开式中第4项与第9项的二项式系数相等,所以 ;所以 ,
由于展开式中项的系数与二项式系数相等,故展开式中系数最大的项为第6项和第7项.
故选:CD.
10. 甲、乙、丙、丁4人每人随机选取VisualBasie、VisualC++,VisualFoxpro三种编程语言之一进行学
习,每种编程语言至少有1人学习,A表示事件“甲学习VisualBasic编程语言”;B表示事件“乙学习
VisualBasic编程语言”;C表示事件“乙学习VisualC++编程语言”,则( )
A. 事件A与B相互独立 B. 事件A与C不是互斥事件
C. D.
【答案】BCD
【解析】
【分析】由古典概率公式求出 ,再利用相互独立事件和互斥事件的
定义判断A,B;用条件概率公式计算判断C,D.
【详解】4人选择3种编程语言之一,每种编程语言至少有1人学习,共有 种安排方案,
甲学习VisualBasic编程语言、乙学习VisualBasic编程语言、乙学习VisualC++编程语言,
各有 种方案,∴ ;甲、乙均学习VisualBasic编程语言,有 种方案,∴ ;
甲学习VisualBasic编程语言且乙学习VisualC++编程语言,有 种方案,∴ ,
对于A,∵ ,∴事件A与B不相互独立,故A错误;
对于B,∵ ,∴事件A与C不是互斥事件,故B正确;
对于C, ,故C正确;
对于D, ,故D正确.
故选:BCD.
11. 已知定义域为 的函数 的导函数为 ,若函数 和 均为偶函数,且
,则( )
A. B. C. D.
【答案】AB
【解析】
【分析】根据题意分析可知4为 的周期,关于 对称,关于点 对称,进而判断AB;分析
可知4为 的周期,但没有充分条件求 ,进而判断CD.
【详解】因为 为偶函数,则 ,
即 ,可知 关于 对称,
又因 为为偶函数,则 ,可知 关于 对称,且 ,则 ,即 ,
可得 关于点 对称,且 ,
则 ,可知4为 的周期,
由 ,可得 ,即 ,
则 ,
即 ,
所以 , ,故AB正确;
因为 ,则 ,即 ,
可知4为 的周期,
又因为 ,则 ,
即 ,可知 关于点 对称,
但没有充分条件求 ,故无法求CD选项的值,故CD错误;
故选:AB.
【点睛】方法点睛:函数的性质主要是函数的奇偶性、单调性和周期性以及函数图象的对称性,在解题中
根据问题的条件通过变换函数的解析式或者已知的函数关系,推证函数的性质,根据函数的性质解决问题.
三、填空题:本题共3小题,每小题5分,共15分.
12. 已知随机变量 的分布列 ,则 ______.
【答案】 ##
【解析】
【分析】根据分布列的性质概率之和为 可求.【详解】已知 ( ),
则由分布列的性质可得
,
解得 ,
故答案为: .
13. 已知 是函数 的两个极值点,若 ,且 的极小值为整
数,则 ______.
【答案】 ##
【解析】
【分析】因为 有两个极值点,所以 有两个变号解,结合韦达定理得出
,又因为 ,联立得出 又因为 ,所以得出
或 再利用 的极小值为整数即可得出答案.
【详解】 由题意知 是 的两根,所以
且 又 所以
所以 即 解得 或当 时, 此时 的极小值为 不合题意;
当 时, 此时 的极小值为 符合题意.
故
故答案为: .
14. 五一小长假,多地迎来旅游高峰期,各大旅游景点都推出了种种新奇活动以吸引游客,小明去某景点
游玩时,发现了一个趣味游戏,游戏规则为:一个会走路的机器人从一数轴上的原点出发沿该数轴行走,
游客可以设定机器人总共行走的步数n,机器人每一步会随机选择前或向后行走,且每一步的距离均为一
个单位,设机器人走完设定的n步后所在位置对应数为随机变量 ,则 __________,
__________.
【答案】 ①. ##0.3125 ②.
【解析】
【分析】X表示向右移动的次数,则 ,再根据二项分布即可得到回到原点的概率,找到
与X关系,得到 ,由二项分布的方差结合方差性质再计算方差即可.
【详解】设X表示向右移动的次数,则 .
若运动6步回到原点,则向左,右各移动3次,
所以回到原点的概率 .
因为机器人走完设定的n步后所在位置对应数为随机变量 ,X表示向右移动的次数则 表示向左移动的次数,
则 ,
则 ,
所以 .
故答案为: ; .
四、解答题:本题共5小题,共77分.解答应写出文字说明、证明过程或演算步骤.
15. 已知 .
(1)若 ,求 的值;
(2)若 ,求m的值.
【答案】(1)
(2) 或
【解析】
【分析】(1)通过赋值法求系数和;
(2)通过二项式定理的通项求参数值.
【小问1详解】
在 中,
取 ,得 ,
取 ,得 ,
以上两式相减,得 .
【小问2详解】
的通项为 ,若 ,可得 ,
所以 ,解得 或 .
16. 已知函数 .
(1)求 在点 处的切线方程;
(2)求函数 的极值.
【答案】(1)
(2)极大值为 ,极小值为 .
【解析】
【分析】(1)求出函数的导数,根据导数的几何意义,即可求得答案;
(2)通过函数的导数研究函数的单调性,再求出函数极值点,求得极值.
【小问1详解】
由 , 的定义域为 ,
得 ,
所以 ,又 ,
所以 在点 处的切线方程为 ,即 ;
【小问2详解】
,
由 ,得 ,或 ,
当 或 时, , 在 上均单调递增;
当 时, , 在 上单调递减;故函数 在 处取得极大值,极大值为 ;
在 处取得极小值,极小值为 .
故函数 有极大值,也有极小值,极大值为 ,极小值为 .
17. 光明高级中学高三年级理科考生800人都参加了本学期的期中调研测试,学校把本次测试数学成绩达
到120分以上(包含120分)的同学的数学成绩等第定为优秀,物理成绩达到90分以上(包含90分)的
同学的物理成绩等第定为优秀.现从理科考生中随机抽取10名同学调研本次测试的数学和物理成绩,如下
表:
8
数学(分) 119 145 99 95 135 120 122 130 120
5
8
物理(分) 84 90 82 84 83 81 83 90 82
1
(1)试列出 列联表,并依据 的独立性检验分析能否认为本次测试理科考生的数学成绩的等
第优秀与物理成绩的等第是否优秀有关?
(2)如果本次测试理科考生的物理成绩 ,用样本估计总体,以10名同学物理成绩的平均
数为 ,方差为 ,若从参加考试的800名理科考生中随机抽取4人,求这4人中至少有1人的物理成绩
的等第优秀的概率.
参考数据:取 , , , .若 ,则
, ,
.
, .
0.10 0.05 0.025 0.010 0.005.
2.706 3.841 5024 6.635 7.879
【答案】(1)答案见解析
(2)
【解析】
【分析】(1)根据题意完善 列联表,求 ,并与临界值对比分析;
(2)根据题意求平均数和方差,结合正态分布求 ,进而利用对立事件分析求解.
【小问1详解】
由题意可得: 列联表为
物理优秀 物理非优秀 总计
数学优秀 2 4 6
数学非优
0 4 4
秀
总计 2 8 10
零假设 :数学成绩的等第优秀与物理成绩的等第优秀无关,
可得 ,
的
依据小概率值 独立性检验,可以推断 成立,
即数学成绩的等第优秀与物理成绩的等第优秀无关.
【小问2详解】
由题意可得,物理成绩的平均分为 (分);
方差
,结合题意可知: ,即 ,则 ,
可得 ,
记“4人中至少1人物理成绩的等第优秀”为事件A,则 为“ 人物理成绩的等第都是非优秀”,
故 ,
所以4人中至少1人物理成绩的等第优秀的概率为 .
18. 2024年4月25日—4月29日,“与辉同行”开启了一场深入中原的文化之旅,让河南文旅打开了流量密
码.某景区趁此时机,举行五一游该景区网上购票抽奖活动,在网上购买该景区门票的游客,可通过手机
扫景区提供的二维码进入抽奖活动页面,每张门票可从6个减免红包中随机抽取2个,6个红包的金额分
别为5元、5元、10元、10元、30元、60元,已知该景区门票每张120元,全部实行网上购票.
(1)记购买1张门票的游客通过抽奖获得的红包金额之和为X,求X的分布列与期望;
(2)已知每位游客除门票外平均在该景区消费30元、40元、60元的概率分别为 , , ,举行此抽
奖活动后预计可使该景区五一期间客流量增加40%,假设每位购票游客都进行了抽奖,回答下列问题并说
明理由:
①举行抽奖活动后该景区在五一期间的门票收入是增加了,还是减少了?
②举行抽奖活动后该景区在五一期间的总收入是增加了,还是减少了?
【答案】(1)分布列见解析,40
(2)①减少了;②增加了
【解析】
【分析】(1)问先求随机变量的分布列,再求期望;
(2)问通过随机变量的期望求总收入,再判断总收入是否增加.
【小问1详解】
由题意得X的取值可以是10,15,20,35,40,65,70,90.
, ,
, ,, ,
, ,
所以X的分布列为
X 10 15 20 35 40 65 70 90
P
【小问2详解】
①假设不举行抽奖活动,该景区在五一期间客流量为n人,则门票收入为120n元,
举行抽奖活动后该景区在五一期间门票收入为 ,
所以举行抽奖活动后该景区 在五一期间门票收入减少了.
②每位游客除门票外平均在该景区消费30元、40元、60元的概率分别为 , , ,
则期望值为 .
不举行抽奖活动,该景区在五一期间总收入为 ,
举行抽奖活动后该景区在五一期间总收入为 ,
所以举行抽奖活动后该景区在五一期间总收入增加了
19. 定义:若函数 与 的图象在 上有且仅有一个交点,则称函数 与 在 上
单交,此交点被称为“单交点”.已知函数 , , .(1)讨论函数 的单调性;
(2)当 时,
(i)求证:函数 与 在上存在“单交点” ;
(ⅱ)对于(i)中的正数 ,证明: .
【答案】(1)答案见解析
(2)(i)证明见解析;(ii)证明见解析;
【解析】
【分析】(1)借助导数,分 及 讨论即可得;
(2)(i)结合定义,令 ,构造函数 ,借助导数研究其单调性,
结合零点的存在性定理即可得证;(ⅱ)原问题可转化为证明 ,构造函数
,借助导数求出其在 上的最大值即可得.
【小问1详解】
,
当 时, 对任意 恒成立,故函数 在 上单调递增;
当 时,令 ,得 ;令 ,得 ,
故函数 在 上单调递减,在 上单调递增;
【小问2详解】
(i)令 ,得 ,得 ,
设 ,则 ,
设 ,则 ,当 时, , 单调递减,
即 在 上单调递减,且 , ,
故 ,使得 ,
当 时, ,函数 单调递增,
当 时, ,函数 单调递减,
因为 , ,
所以 在 上只有一个零点 ,故函数 在 上只有一个零点 ,
即函数 与 在 上存在“单交点” ;
(ii)因为 ,所以要证 ,即证 ,
即证 ,只需证 ,
因为 ,得 ,
所以只需证 即可,
令 , ,则 ,
当 时, , 单调递增,
当 时, , 单调递减,
故 ,即 ,
原不等式即证.
【点睛】关键点点睛:最后一问关键点在于借助 ,从而消去参数 ,将
转化为 .