文档内容
专题5.2 导数的运算
知识储备
1.基本初等函数的导数公式
基本初等函数 导函数
f(x)=c(c为常数) f′(x)=0
f(x)=sin x f′(x)=cos_x
f(x)=ex f′(x)=
f(x)=ln x
f′(x)=
f(x)=xα(α∈Q*) f′(x)= αx α - 1
f(x)=cos x f′(x)= - sin _x
f(x)=ax(a>0,a≠1) f′(x)= a x ln _a
f(x)=log x(a>0,a≠1)
a
f′(x)=
2.导数的运算法则
(1)[f(x)±g(x)]′= f ′ ( x )± g ′ ( x ) ;
(2)[f(x)·g(x)]′= f ′ ( x ) g ( x ) + f ( x ) g ′ ( x ) ;
(3) (g(x)≠0).
3.复合函数导数的运算法则
概念:一般地,对于两个函数y=f(u)和u=g(x),如果通过中间变量u,y可以表示成x的函数,那
么称这个函数为函数y=f(u)和u=g(x)的复合函数,记作y= .
求导法则:一般地,对于由函数y=f(u)和u=g(x)复合而成的函数y=f(g(x)),它的导数与函数y=
f(u),u=g(x)的导数间的关系为y′= .即y对x的导数等于 对 的导数 与对 的导
x
数的乘积.
4.常用结论
1.f′(x)代表函数f(x)在x=x 处的导数值;(f(x))′是函数值f(x)的导数,且(f(x))′=0.
0 0 0 0 0
2. ′=- .
3.曲线的切线与曲线的公共点的个数不一定只有一个,而直线与二次曲线相切只有一个公共点.
4.函数y=f(x)的导数f′(x)反映了函数f(x)的瞬时变化趋势,其正负号反映了变化的方向,其大小|f′(x)|
反映了变化的快慢,|f′(x)|越大,曲线在这点处的切线越“陡”.能力检测
注意事项:
本试卷满分100分,考试时间45分钟,试题共16题.答卷前,考生务必用0.5毫米黑色签字
笔将自己的姓名、班级等信息填写在试卷规定的位置.
一、单选题
1.(2020·全国高二课时练习)对于函数 ,若 ,则实数 等于(
)
A. B. C. D.
【答案】A
【解析】 , ,
所以 ,解得 ,故选:A.
2.(2020·全国高二课时练习)已知 ,则 ( )
A. B. C. D.
【答案】D
【解析】由题意,得 ,则 ,故选:D.
3.(2020·全国高二课时练习)下列求导运算正确的是( )
A. B.
C. D.
【答案】C
【解析】 ,故A不正确;
,故B不正确;,故C正确;
,故D不正确.故选:C.
4.(2020·山西高三期中(文))已知函数 ,其中 为函数 的导
数,则 ( )
A. B. C. D.
【答案】B
【解析】 ,
所以, ,
,函数 的定义域为 ,
,
所以,函数 为偶函数,
因此, .故选:B.
5.(2020·四川省广元市川师大万达中学高三月考(理))已知 是定义在 上的偶函数,当
时, (其中 为 的导函数),若 ,则的解集为( )
A. B. C. D.
【答案】A
【解析】由 ,而 知: 在 上单调减,而
,即 ,又 知: ,
∴在 上有 ,又 是定义在 上的偶函数,则 在 上为偶函数,∴
在 上单调增,即 ,可得 ,综上,有 ,故选:
A
6.(2020·湖南长沙市·长郡中学高二期中)若函数 , 满足 ,且
,则 ( )
A.1 B.2 C.3 D.4
【答案】C
【解析】因为函数 , 满足 ,且 ,
所以 ,则 ,
对 两边求导,
可得 ,
所以 ,因此 .故选:C.7.(2020·安徽淮北市·淮北一中高二期中)等比数列 中, , ,函数
,则 ( )
A.26 B.29 C.212 D.215
【答案】C
【解析】等比数列 中, , ,
所以 ,
因为函数 ,
,
则 .故选:C.
8.(2020·江西抚州市·临川一中高二期中(文))设函数 ,则“
”是“ ”的( )
A.充分不必要条件 B.必要不充分条件 C.充要条件 D.既不充分也不必要条件
【答案】A
【解析】 ,
当 时, , ,满足充分性.
当 ,即 ,解得 或 ,不满足必要性 .
所以“ ”是“ ”的充分不必要条件.故选:A
二、多选题
9.(2020·江苏南通市·高三期中)北斗卫星导航系统是中国自行研制的全球卫星导航系统,可在全
球范围内为各类用户提供全天候、全天时、高精度、高定位、导航、授时服务,2020年7月31日
上午,北斗三号全球卫星导航系统正式开通,北斗导航能实现“天地互通”的关键是信号处理,其中某语言通讯的传递可以用函数 近似模拟其信号,则下列结论中正确的
是( )
A.函数 的最小正周期为
B.函数 的图象关于点 对称
C.对任意 ,都有
D.函数 的最小值为-3
【答案】BCD
【解析】A.因为 的周期分别是 ,其最小公倍数为 ,所
以函数函数 的最小正周期为 ,故错误;
B.因为 ,故正确;
C. ,故正确;
D. ,故正确;故选:BCD
10.(2020·全国高二课时练习)(多选)已知函数 及其导数 ,若存在 ,使得
,则称 是 的一个“巧值点”.下列函数中,有“巧值点”的是( )
A. B. C. D.
【答案】ACD
【解析】在A中,若 ,则 ,则 ,这个方程显然有解,故A符合要求;在B中,若 ,则 ,即 ,此方程无解,故
B不符合要求;
在C中,若 ,则 ,由 ,令 , ( ),作出两函数的
图像如图所示,由两函数图像有一个交点可知该方程存在实数解,故C符合要求;
在D中,若 ,则 ,由 ,可得 ,故D符合要求.故选:
ACD.
11.(2020·湖北高三月考)已知函数 ,其导函数为 ,
则( )
A. B. C. D.
【答案】BC
【解析】因为 ,所以 .
因为 ,所以 .
故 .故选:BC
12.(2020·山东高三专题练习)以下函数求导正确的是( )A.若 ,则 B.若 ,则
C.若 ,则 D.若 ,则
【答案】AC
【解析】对A, ,故A正确
对B, ,故B错
对C,
所以C正确
对D, ,故D错.故选:AC
三、填空题
13.(2020·广东中山市·高二期末)在许多实际问题中,一个因变量往往与几个自变量有关,即因
变量的值依赖于几个自变量,这样的函数称为多元函数.例如,某种商品的市场需求量不仅仅与其
市场价格有关,而且与消费者的收入以及这种商品的其他代用品的价格等因素有关,即决定该商品
需求量的因素不止一个而是多个.我们常常用偏导数来研究多元函数.以下是计算二元函数
在 处偏导数的全过程:
, ,所以 ,
,由上述过程,二元函数 ,则______.
【答案】
【解析】根据题意,得到 , ,
则 , ,
因此 .故答案为: .
14.(2020·全国高三其他模拟(理))给出下列四个命题:
①命题“ , ”的否定是“ , ”;
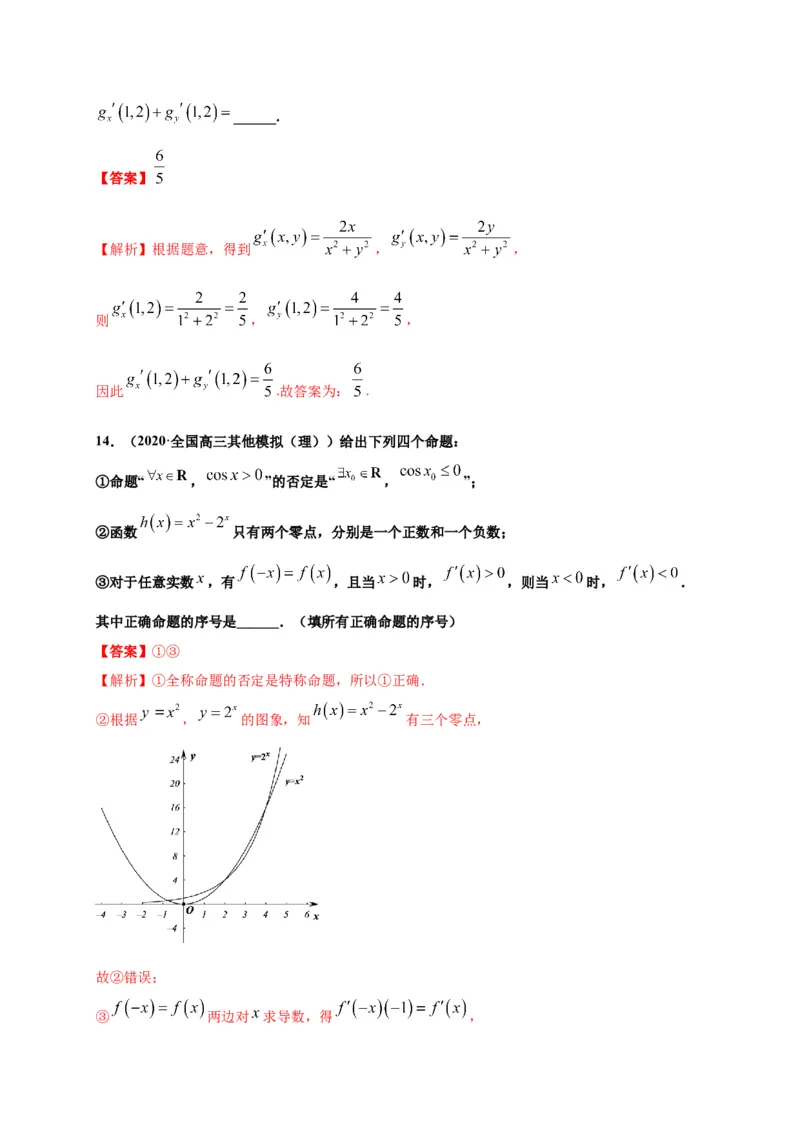
②函数 只有两个零点,分别是一个正数和一个负数;
③对于任意实数 ,有 ,且当 时, ,则当 时, .
其中正确命题的序号是______.(填所有正确命题的序号)
【答案】①③
【解析】①全称命题的否定是特称命题,所以①正确.
②根据 , 的图象,知 有三个零点,
故②错误;
③ 两边对 求导数,得 ,所以 是奇函数,当 时, ,
当 时, .所以③正确.故答案为:①③
15.(2020·全国高二课时练习)已知函数 、 满足 , , ,
,若 ,则 _________.
【答案】
【解析】 , ,
由 , , , ,
得 .故答案为: .
四、双空题
16.(2020·浙江宁波市·高二期末)已知函数 和点 ,则导数
______; 的图像在点 处的切线的方程是______.
【答案】
【解析】因为 ,
所以 ,
因为 , ,
所以 的图像在点 处的切线的方程是 ,即 ,
故答案为: ; .