专题09直线与圆、圆与圆的位置关系（解析版）_E015高中全科试卷_数学试题_选修1_06.专项练习_专题09直线与圆、圆与圆的位置关系-高中数学新教材人教A版选择性必修配套提升训练

专题09 直线与圆、圆与圆的位置关系 一、单选题 2,1 x 1．（2020·北京高三零模）圆心为 且和 轴相切的圆的方程是（ ） x22 y12 1 x22 y12 1 A． B． x22 y12 5 x22 y12 5 C． D． 【答案】A 【解析】 圆心为 2,1 且和 x 轴相切的圆的半径为1，因此，所求圆的方程为 x22 y12 1 . 故选：A. 3x4y40 (x3)2  y2 9 2．（2019·甘南藏族自治州合作第一中学高一期末）直线 被圆 截得的弦长 为（ ） 2 2 4 4 2 2 A． B． C． D． 【答案】C 【解析】 因为圆心为（3,0），半径为3，那么利用圆心到直线的距离公式 33404 d  1 5 ，利用勾股定理可知弦长为2 r2 d2 2 8 4 2． 选C y  xm x2 2x y2 30 A、B 3．（2020·湖南省高三一模（文））已知直线 与圆 交于 两点，且 | AB|2 2 m ，则 （ ） 1  3 3 A． 或3 B． C． D．1或 【答案】D 【解析】x12  y2 4 1,0 圆的方程可化为： ，圆心是 ，半径r=2， |1m| d  设圆心(1,0)到直线y  xm的距离为d ， 2 ， m12  24 2 ，m12,m1或 3 . 故选：D. C A(0,2) B(4,6) C 4．（2020·全国高三月考（文））已知圆 经过两点 ， ，且圆心 在直线 l:2x y30 C 上，则圆 的方程为（ ） x2  y2 6y160 x2  y2 2x2y80 A． B． x2  y2 6x6y80 x2  y2 2x2y560 C． D． 【答案】C 【解析】 62 1 因为线段AB的中点坐标为(2,4)，直线AB的斜率为40 ，所以线段AB的垂直平 y4 (x2) y 6x l (3,3) 分线方程为 ，即 与直线 方程联立，得圆心坐标为 .又圆 的半径 r  (30)2 (32)2  10 ，所以，圆C的方程为 (x3)2 (y3)2 10 ， x2  y2 6x6y80 即 . 故选：C. x2  y2 2 x y40 5．（2019·全国高二月考（文））圆心在圆 上，与直线 相切，且面积最大的圆的 方程为（ ） (x1)2 (y1)2 2 (x1)2 (y1)2 2 A． B． (x1)2 (y1)2 18 (x1)2 (y1)2 18 C． D．【答案】C 【解析】 x2  y2 2 x y40 y  x 如图，过圆 的圆心(原点)作直线 的垂线 ， x2  y2 2 A ,B. 垂线与圆 的交点为 y  x x2  y2 2 B 易知当圆心在点 时，所求圆的半径最大，圆的面积也最大.联立 和 ， B1,1, B1,1 求得 所以圆的半径最大时，圆心为 ， 114 3 2 又由点到直线的距离公式求得点 B 到直线x  y4 0的距离为 12 12 ， x12 y12 18. 即所求圆的半径r 3 2 ，所以所求面积最大的圆的方程为 故选：C. P(2,1) C：x2  y2 8x0 MN MN 6．（2019·全国高二月考（文））已知点 为圆 的弦 的中点，则弦 所在 直线的方程为（ ） 2x y50 x2y40 2x y30 x2y 0 A． B． C． D． 【答案】C 【解析】 C:x2  y2 8x 0 x42  y2 16, C4 ,0 圆 的标准方程为 则圆心为 ， 10 1 k   直线PC的斜率 PC 24 = 2 ，又PC MN ，所以 k k 1 ，所以 k 2 ， PC MN MNy12x2 2x y30 故弦MN所在直线的方程为 即 . 故选：C. P:x2  y2 4x2y30 3xmy 0(mR) 7．（2020·河南省高二月考（文））已知圆 与直线 相交 A,B APB90 m 于 两点，且 ，则 的值为( ) A．0 B．4 C．0或4 D．0或1 【答案】C 【解析】 P x2  y2 4x2y30  为圆 的圆心， ∴ P(2,1) r 2 2 ，圆半径 ， |32m| d  2 又 APB90，  圆心到直线3xmy 0的距离 32 m2 ，  m0 解得 或4， 故选：C. 8．（2019·甘南藏族自治州合作第一中学高一期末）点P在圆C ：x2+y2﹣8x﹣4y+11=0上，点Q在圆C ： 1 2 x2+y2+4x+2y+1=0上，则|PQ|的最小值是（ ） 5 5 5 A．5 B．3 C．3 5 D．3 5 【答案】C 【解析】 x2  y2 8x4y110 x42 y22 9 圆 化为标准方程为 ， 圆心为C (4,2)，半径为3； 1 x2  y2 4x2y10 x22 y12 4 圆 化为标准方程为 , 圆心为C (−2,−1)，半径为2， 2 ∴两圆的圆心距为 CC  242 122  369  45 3 5 5， 1 2∴两圆外离， 5 ∴|PQ|的最小值是两圆的圆心距减去半径的和,即3 5， 故选：C. C :(x2)2  y2 9 9．（2020·宜宾市叙州区第二中学校高三月考（理））已知圆 1 与圆 C :(x1)2 (y4)2  r2(r 0) r 2 有公共点，则 的取值范围是（ ） [2,8] [2,13] (0,13] (0,8] A． B． C． D． 【答案】A 【解析】 C :(x2)2  y2 9 C 2,0, R 3 圆 1 的圆心 1 半径 1 ， C :(x1)2 (y4)2  r2(r 0) C 1,4, R r 圆 2 的圆心 2 半径 2 ，且两圆的圆心距为 CC  212 042 5， 1 2 r3 5r3 要使两个圆有公共点，则需满足 ，解得 2r 8 ，所以r的取值范围是 2r 8 ， 故选：A. (xa)2 (ya)2 9a 0 O 10．（2019·全国高二月考（文））若圆 上总存在两点到原点 的距离为 a 1，则实数 的取值范围是（ ）     0,1 2,2 2,2 2 2,4 A． B． C． D． 【答案】C 【解析】 (x+a)2+(y+a)2＝9a 0 O 由题意，圆 上总存在两点到原点 的距离为1， xa2 ya2 9 x2  y2 1 即为圆 和圆 相交， 又由两圆圆心距d  a02 a02  2 a ，31 2a31 2 a2 2 则 ，解得 ，   2,2 2 即实数a的取值范围是 . 故选：C. 二、多选题 11．（2019·辽宁省高二月考）已知 分别为圆 ： 与圆 ： 上的动点， 为 轴上的动点，则 的值可能是（ ） A．7 B．8 C．9 D．10 【答案】CD 【解析】 圆 ，关于 轴对称的圆为圆 ， 则 的最小值为 ，又 ， 故选： . 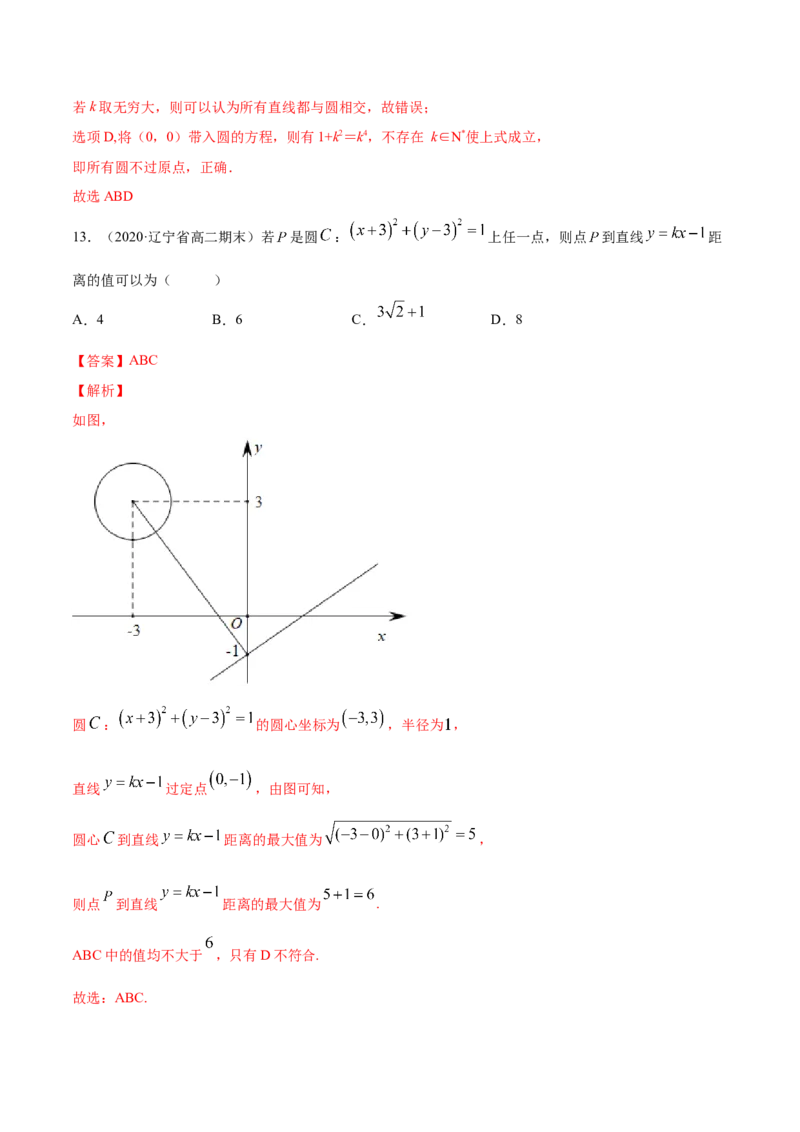12．（2020·江苏省启东中学高一开学考试）设有一组圆 .下列四个命 题正确的是（ ） A．存在 ，使圆与 轴相切 B．存在一条直线与所有的圆均相交 C．存在一条直线与所有的圆均不相交 D．所有的圆均不经过原点 【答案】ABD 【解析】 根据题意得圆的圆心为（1，k），半径为 ， 选项A,当k= ，即k=1时，圆的方程为 ，圆与x轴相切，故正确； 选项B，直线x=1过圆的圆心（1，k），x＝1与所有圆都相交，故正确； 选项C,圆k：圆心（1，k），半径为k2，圆k+1：圆心（1，k+1），半径为（k+1）2， 两圆的圆心距d＝1，两圆的半径之差R﹣r＝2k+1，（R﹣r＞d），∁k 含于C k+1 之中，若k取无穷大，则可以认为所有直线都与圆相交，故错误； 选项D,将（0，0）带入圆的方程，则有1+k2＝k4，不存在 k∈N*使上式成立， 即所有圆不过原点，正确． 故选ABD 13．（2020·辽宁省高二期末）若 是圆 ： 上任一点，则点 到直线 距 离的值可以为（ ） A．4 B．6 C． D．8 【答案】ABC 【解析】 如图， 圆 ： 的圆心坐标为 ，半径为 ， 直线 过定点 ，由图可知， 圆心 到直线 距离的最大值为 ， 则点 到直线 距离的最大值为 . ABC中的值均不大于 ，只有D不符合. 故选：ABC.三、填空题 x2  y2 4y 0 14．（2019·浙江省高二期中）过原点且倾斜角为60的直线与圆 相交，则圆的半径为 ___________直线被圆截得的弦长为______________ 【答案】 【解析】 x2  y2 4y 0 将圆 的方程化为标准式为 ，所以该圆圆心为（0,2）的半径为2；过原点 且倾斜角为 的直线方程为 ，该直线与圆心的距离 ，直线被圆截得的弦长为 60 15．（2019·江苏省高二期末（文））已知圆 ，过点 的直线与圆交于A，B两点且 ，则弦AB的长为______． 【答案】3. 【解析】 如图：取AB的中点M，则由 可得 ， ，在直角三角形OMB中有： ，即 ， 在直角三角形OMP中有： ，即 ②， 联立①②解得 ， 故答案为：3． 16．（2020·吉林省高三月考（理））已知点 ， ，点 在圆 上， 则使 的点 的个数为__________. 【答案】1 【解析】 由题意可得，若 则点 在以 为直径的圆上， 此时点 的轨迹是 ， 且点 在圆 上， 即点P为圆 与圆 的交点， 考查两圆的圆心距： ， 两圆的半径： ，满足： ， 即两圆外切，据此可得：点 的个数为1个. 17．（2018·江苏省高三月考）已知过点 的直线 被圆 截得的弦长为 ，则直线 的方程是 ________. 【答案】 或 【解析】 圆的标准方程为 ，圆心坐标为 ，半径为 ，由题意可知，圆心到直线 的距离为 . ①当直线 的斜率不存在时，直线 的方程为 ，此时圆心到直线 的距离 ，符合题意； ②当直线 的斜率存在时，设直线 的方程为 ，即 ， 圆心到直线 的距离为 ，解得 ， 此时，直线 的方程为 ，即 . 综上所述，直线 的方程为 或 . 故答案为： 或 . 四、解答题 18．（2019·陕西省高二竞赛）已知平面直角坐标系中的点 的坐标x，y满足 ，记 的最大值为M，最小值为m. （1）请说明P的轨迹是怎样的图形； （2）求 值. 【答案】（1）以 为圆心，3为半径的圆；（2）72 【解析】 （1）由 知， .因此，点P的轨迹是以 为圆心，3 为半径的圆. （2） ， 设 ，则 .∵ ， . ∴ ， ， . 19．（2019·全国高二月考（文））已知点 ，圆 （1）若过点A只能作一条圆C的切线，求实数a的值及切线方程； （2）设直线l过点A但不过原点，且在两坐标轴上的截距相等，若直线l被圆C截得的弦长为2 ，求实 数a的值. 【答案】（1） ，切线方程： 或 ，切线方程： ；（2） 或 【解析】 （1） 过点 只能作一条圆 的切线 在圆 上 ，解得： 当 时， ，则切线方程为： ，即 当 时， ，则切线方程为： ，即 （2）设直线 方程为： 直线 方程为： 圆 的圆心到直线距离 ，解得： 或 点睛：直线与圆问题的常用结论： 1.过圆 上一点 的切线方程为： ；2.直线被圆截得的弦长等于 . 20．（2019·浙江省高二期中）已知圆C： ，点 为圆内的一点，直线l与 圆C相交于A，B两点，且点P恰好为弦 的中点. （1）求实数a的取值范围以及直线l的方程； （2）若以 为直径的圆过原点O，求圆C的方程 【答案】（1） ； （2） 【解析】 （1）圆的标准方程为 ，则圆心 ，半径 （ ）， ∵弦 的中点为 ，∴点P在圆内部，即 ， ∴ ，即 . ∵弦的中点为 ，∴直线 的斜率为 ，则直线l的斜率 . 则直线l的方程为 ，即 . （2）由圆C： ，与 ， 联立得： ，即 ， 设 ， ，故 ， . 由 . 得： ，故C： . 21．（2019·吉林省长春外国语学校高二月考）已知圆 内有一点 ， 为过点 且倾斜角为 的弦（1）当 时，求弦长 ； （2）当弦 被点 平分时，求直线 的方程. 【答案】（1） ；（2） 【解析】 圆 的方程可化为： ， 则 ，半径 ， 当 时，直线 的斜率为1， 则直线方程为 ， 则圆心到直线的距离 ， 所以弦长 ； （2）设直线 的斜率为 ，根据条件可知 ， 则 ， 所以 ， 则直线 的方程为 ， 即 ． 22．（2019·甘南藏族自治州合作第一中学高一期末）在平面直角坐标 中，圆 与圆 相交与 两点．（I）求线段 的长． （II）记圆 与 轴正半轴交于点 ，点 在圆C上滑动，求 面积最大时的直线 的方程． 【答案】（I） ；（II） 或 ． 【解析】 （I）由圆O与圆C方程相减可知，相交弦PQ的方程为 ． 点（0，0）到直线PQ的距离 ， （Ⅱ） ， . 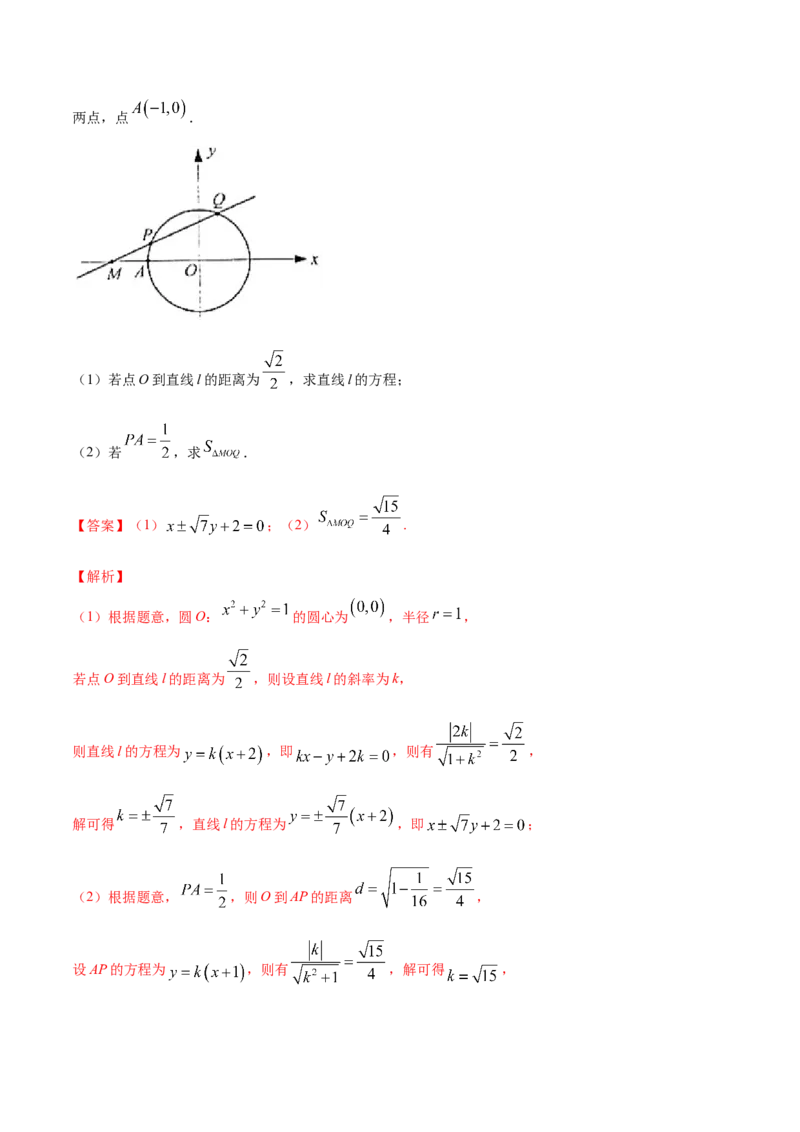当 时， 取得最大值． 此时 ，又 则直线NC为 ． 由 ， 或 当点 时， ，此时MN的方程为 ． 当点 时， ，此时MN的方程为 ． ∴MN的方程为 或 ． 23．（2019·江苏省高二期末（文））如图，已知圆O： ，过 的直线l与圆交于P，Q两点，点 ． （1）若点O到直线l的距离为 ，求直线l的方程； （2）若 ，求 ． 【答案】（1） ；（2） . 【解析】 （1）根据题意，圆O： 的圆心为 ，半径 ， 若点O到直线l的距离为 ，则设直线l的斜率为k， 则直线l的方程为 ，即 ，则有 ， 解可得 ，直线l的方程为 ，即 ； （2）根据题意， ，则O到AP的距离 ， 设AP的方程为 ，则有 ，解可得 ，则AP的方程为 ，与圆O的方程联立，可得 ， 解可得 或 ，则 ，则 ，则P的坐标为 ， 直线MP的方程为 ，与圆O的方程联立可得 ， 解可得 或 ，则 ， ，即Q的坐标为 ， 则 ，O到直线MP的距离 ， 故 ．