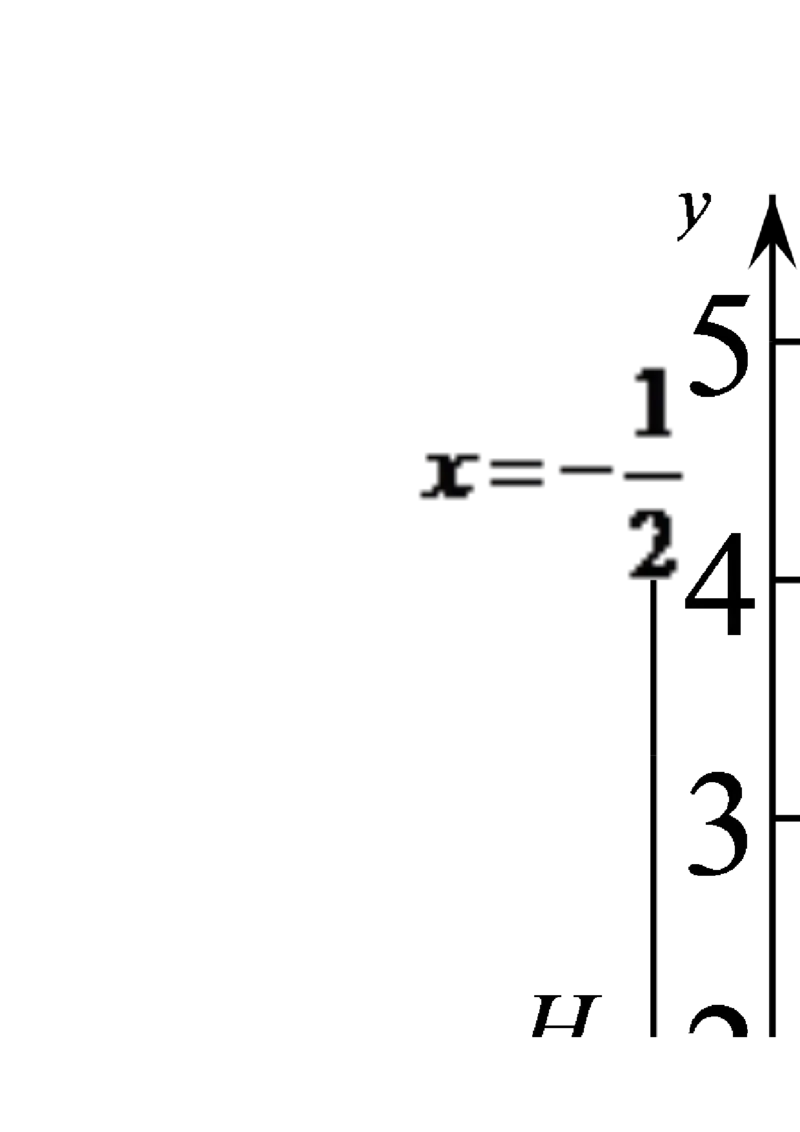专题15圆锥曲线的方程（单元测试卷）（解析版）_E015高中全科试卷_数学试题_选修1_06.专项练习_专题15圆锥曲线的方程（单元测试卷）-高中数学新教材人教A版选择性必修配套提升训练

专题15 《圆锥曲线的方程》单元测试卷
一、单选题
y2 4x
1．（2020·辽宁省高三月考（文））若抛物线 上的点M到焦点的距离为10，则M点到y轴的距离
是（ ）
A．6 B．8 C．9 D．10
【答案】C
【解析】
y2 4x F1，0 x1
抛物线 的焦点 ，准线为 ，由M到焦点的距离为10，
可知M到准线的距离也为10，故到M到的距离是9，故选C．
x2 y2
 1
2．（2019·涟水县第一中学高二月考）椭圆 m 4 的焦距为2，则m的值等于（ ）
5 3 5 3 8
A． B． C． 或 D．
【答案】C
【解析】
x 2 m4 2 m5
若椭圆的焦点在 轴上时，则有 ，解得 ；
y 2 4m 2 m3
若椭圆的焦点在 轴上时，则有 ，解得 .
m5 3
综上所述， 或 .
故选：C.
3．（2018·镇原县第二中学高二期末（文））设抛物线的顶点在原点，准线方程为x=﹣2，则抛物线的方
程是（ ）
A．y2=﹣8x B．y2=8x C．y2=﹣4x D．y2=4x
【答案】B
【解析】
∵准线方程为x=﹣2
∴ =2∴p=4
∴抛物线的方程为y2=8x
故选B
F C: y2 3x F 30 C A B
4．（2020·天津高三一模）设 为抛物线 的焦点，过 且倾斜角为 的直线交 于 ，
AB 
两点，则 （ ）
30
A． 3 B．6 C． 12 D．7 3
【答案】C
【解析】
3 3 3 3
F( ,0) k tan300  y  (x )
由题意，得 4 ．又因为 3 ，故直线AB的方程为 3 4 ，与抛物线y2=3x
联立，得
16x2 168x90
，设
A(x
1
,y
1
),B(x
2
,y
2
)
，由抛物线定义得，
AB  x
1
x
2
 p 
168 3
 12
16 2 ，选C．
ab9 c3
5．（2018·镇原县第二中学高二期末（文））已知 ， ，则椭圆的标准方程是（ ）
x2 y2
x2 y2
 1  1
A．25 9 B．25 16
x2 y2
x2 y2 x2 y2
 1  1  1
C．25 16 或16 25 D．16 9
【答案】C
【解析】
ab9 c3 a2 b2 c2 a2 25 b2 16
由 ， ， ，可解得 ， ，
x2 y2
则当椭圆的焦点在 轴上时，此时椭圆的标准方程为：  1；
x 25 16x2 y2
 1
当椭圆的焦点在y轴上时，椭圆的标准方程为：16 25 .
故选：C
x2 y2
 1b0
6．（2018·镇原县第二中学高二期末（文））双曲线12 b2 的一条渐近线为 2x 3y 0，
则b（ ）
3 2 2
A．3 B．2 C． D．
【答案】D
【解析】
b
y  x
双曲线的焦点在x轴，a2 3，渐近线方程是 a ，而已知一条渐近线为 2x 3y 0，
2 6 b 6
k   
3 3 ，所以 2 3 3 ，解得： b2 2 .
故选：D
1
e
7．（2018·民勤县第一中学高二期末（文））已知椭圆的一个焦点为F（0，1），离心率 2 ，则椭圆的
标准方程为（ ）
x2
y2 x2 y2 x2 y2
 y2 1 x2  1  1  1
A． 2 B． 2 C． 4 3 D． 3 4
【答案】D
【解析】
1 x2 y2
e  1
由题意知c1，又离心率 2 ，所以a2，b2 a2 c2 3，即所求椭圆的标准方程 3 4 ，
故选D．
x2 y2
 1
8．（2019·涟水县第一中学高二月考）设双曲线a2 b2 (a>0，b>0)的虚轴长为2，焦距为2 3，则双曲线的渐近线方程为( )
2
A．y＝± x B．y＝±2x
2 1
C．y＝± 2 x D．y＝±2 x
【答案】C
【解析】
3
由题意知2b=2,2c=2 ,
3 2
∴b=1,c= ,a2=c2-b2=2,a= ,
b 1 2
∴渐近线方程为y=±a x=± 2 x=± 2 x.故选C.
x2 y2
9．（2019·浙江省高二期中）如图，A，
B
，C是椭圆a2

b2
1 ab0
上的三个点，AB经过原
BF 3CF
点 O ， AC 经过右焦点F ，若 BF  AC 且 ，则该椭圆的离心率为（ ）
1 2 3 2
A．2 B． 2 C． 2 D． 3
【答案】B
【解析】F AF,CF,BF BF  AC AFBF
取左焦点 1，连接 1 1 1， ，根据椭圆的对称性可得： 1是矩形，
CF m, CF 2am, BF  AF 3m, AF 2a3m, AC 2a2m
设 1 1 ，
2 2 2
RtAFC AF  AC  CF (3m)2 (2a2m)2 (2am)2
1 中， 1 1 即：
a
m
AF a, AF a
解得： 3 ，则 1
c2 1
2 2 2 a2 2c2, 
在RtAF 1 F 中 AF 1  AF  FF 1 即：a2 a2 (2c)2， a2 2
2
所以椭圆离心率为 2 .
故选：B
x2
 y2 1(a 1)
10．（2018·安徽省合肥一中高三一模（文））已知椭圆a2 的左、右焦点分别为F ，F ，
1 2
A C FA FF AF
是椭圆在第一象限上的一个动点，圆 与 1 的延长线， 1 2的延长线以及线段 2都相切，且
M 3,0
为其中一个切点．则椭圆的离心率为（ ）
3 2 2 2 6
A． 2 B． 3 C． 2 D． 3
【答案】B
【解析】设圆 C 与 F 1 A 的延长线相切于点 N ，与 AF 2相切于点T ，由切线长相等，得 AN  AT ，
FN  FM FT  F M F(c,0) F (c,0)
1 1 ， 2 2 ， 1 ， 2 ，
AF  AF 2a
由椭圆的定义可得， 1 2 ，
 
FN  FM 3c AF + AN 2a AF  AN 2a AN  AT +TF
1 1 1 2 2
2a F M 2a(3c)
2 ，
则2a6，即a3，
b1 c a2 b2 2 2
又 ，所以 ，
c 2 2
e 
因此椭圆的离心率为 a 3 .
故选：B.
二、多选题
11．（2019·山东省青岛二中高二月考）（多选题）下列说法正确的是（ ）
x2 xy  x
A．方程 表示两条直线
x2 y2
 1
B．椭圆10m m2 的焦距为4，则m4
x2 y2
C．曲线  xy关于坐标原点对称
25 9
x2 y2 b
  y  x
D．双曲线a2 b2 的渐近线方程为 a【答案】ACD
【解析】
x2 xy  x xx y10 x0 x y10
方程 即 ，表示 ， 两条直线，所以A正确；
x2 y2
椭圆10m

m2
1 的焦距为4，则10mm24或m210m4，解得m4或
m8
，所以B选项错误；
x2 y2 x2 y2
曲线  xy上任意点Px,y，满足  xy，Px,y关于坐标原点对称点Px,y也满足
25 9 25 9
x2 y2 x2 y2 x2 y2
 xy Px,y  xy  xy
25 9 ，即 在25 9 上，所以曲线25 9 关于坐标原点对称，
所以C选项正确；
x2 y2 b
  y  x
双曲线a2 b2 即0，其渐近线方程为 a 正确，所以D选项正确.
故选：ACD
C F F y
12．（2019·山东省高二期中）已知椭圆 的中心在原点，焦点 1， 2在 轴上，且短轴长为2，离心率
6
为 3 ，过焦点F 1 作y轴的垂线，交椭圆C于 P ，Q两点，则下列说法正确的是（ ）
y2 x2
x2 1  y2 1
A．椭圆方程为 3 B．椭圆方程为 3
2 3
PQ 
C． 3 D．PFQ的周长为4 3
2
【答案】ACD
【解析】c 6

由已知得，2b=2，b=1，a 3 ，
a2 b2 c2 a2 3
又 ，解得 ，
y2
x2 1
∴椭圆方程为 3 ，
如图：
2b2 2 2 3
PQ   
∴ a 3 3 ，PFQ的周长为 4a4 3 ．
2
故选：ACD．
3
  y  x
3, 2
13．（2019·江苏省苏州实验中学高二月考）已知双曲线C过点 且渐近线为 3 ，则下列结
论正确的是（ ）
x2
 y2 1
A．C的方程为 3 B．C的离心率为 3
y ex2 1 C x 2y10 C
C．曲线 经过 的一个焦点 D．直线 与 有两个公共点
【答案】AC
【解析】
3 1 1
y  x y2  x2 x2  y2 
对于选项A：由已知 3 ，可得 3 ，从而设所求双曲线方程为3 ，又由双曲线1
 3, 2  32 ( 2)2 
C过点 ，从而3 ，即1，从而选项A正确；
c 2 2 3
e  
对于选项B：由双曲线方程可知 a  3 ， b1 ， c2 ，从而离心率为 a 3 3 ，所以B选项
错误；
2,0 y ex2 1
对于选项C：双曲线的右焦点坐标为 ，满足 ，从而选项C正确；
x 2y10

对于选项D：联立
x2
，整理，得 ，由 ，知直线与
  y2 1
 3 y2-2 2y20 (2 2)2 420
C
双曲线 只有一个交点，选项D错误.
故选AC
三、填空题
x2
 y2 1
14．（2019·江苏省高三三模）双曲线 2 的焦距为______.
2 3
【答案】
【解析】
x2
 y2 1
双曲线 2 的焦距为2c2 a2 b2 2 3.
2 3
故答案为： .
x2 y2
15．（2019·重庆巴蜀中学高二期中（理））若双曲线  1的左焦点在抛物线 y2 2px 的准线上，
5 4
p
则 的值为________.
【答案】6
【解析】
x2 y2 p
双曲线 5

4
1
的左焦点为
3,0
，即
-
2
=-3
，故 p=6.6
故答案为： .
x2 y2
C：  1
16．（2020·浙江省高三二模）已知椭圆 9 7 ，F为其左焦点，过原点O的直线l交椭圆于A，B
两点，点A在第二象限，且∠FAB＝∠BFO，则直线l的斜率为_____．
7

【答案】 3
【解析】
x 2 y 2
设Ax 0 ,y 0  ，则Bx 0 ,y 0  ，x 0 0，y 0 0且 9 0  7 0 1 ，
∵F为其左焦点，
y y
  tanBFO 0 k  0
∴F  2,0 ， x  2 ，直线AB的斜率 1 x ．
0 0
y
k  0
经分析直线AF的斜率必存在，设为 2 x  2 ，
0
k k 2y
tanFAB  1 2  0
则 1k k x 2  2x  y 2 ，
1 2 0 0 0
2y y
0  0
又 FABBFO ，∴ x 2  2x  y 2 x  2 ，
0 0 0 0
x 2 y 2 3 2 14
0  0 1 x  y 
∴x 2 2 2x  y 2 2，又 9 7 ，x (3,0)，可解得： 0 2 ， 0 2 ，
0 0 0 0
y 7
0 
∴直线l的斜率为 x 3 ．
0
7

故答案为： 3 ．
17．（2019·乐清市知临中学高二期末）已知抛物线 y2 2x 的焦点为F ，定点 A3，2 .若抛物线上存在一M MA  MF M
点 ，使 最小，则点 的坐标为________，最小值是______.
7
2，2
【答案】 2
【解析】
MH
根据题意，作 垂直于准线，画出几何关系如下图所示：MF  MH
根据抛物线定义可知， ，
A,M,H MA  MF
因而当 在同一直线上时， 的值最小，
7
此时 MA  MF  AH  ，
2
M 42x
的纵坐标为2，代入抛物线解析式可知 ，
M 2,2
所以M 的横坐标为2，即 ，
7
M 2,2
故答案为： ，2 ；
四、解答题
x2 y2
 1a0,b0
18．（2018·镇原县第二中学高二期末（文））已知双曲线a2 b2 的一条渐近线方程是
y  3x y2 24x
，它的一个焦点在抛物线 的准线上.
（1）求双曲线的焦点坐标；
（2）求双曲线的标准方程.
x2 y2
 1
【答案】（1）F6,0
；（2） 9 27
【解析】
y2 24x x6
因为抛物线 的准线方程为 ，
F 6,0
则由题意得，点 1 是双曲线的左焦点.
F6,0
（1）双曲线的焦点坐标 .
a2 b2 c2 36
（2）由（1）得 ，
y  3x
又双曲线的一条渐近线方程是 ，b
 3
所以a ，解得a2 9，b2 27，
x2 y2
 1
所以双曲线的方程为： 9 27 .
y2 2px(p 0) F M
19．（2019·湖南省衡阳市八中高二月考）已知抛物线 的焦点为 ，点 在抛物线上，
MF 5
且点M 的横坐标为4， ．
（1）求抛物线的方程；
F 45 l A、B AB
（2）设过焦点 且倾斜角为 的 交抛物线于 两点，求线段 的长．
y2 4x 8
【答案】（1） ；（2） .
【解析】
p
MF 4 5
（1）由题意得 2 ，
p 2 y2 4x
∴ ，故抛物线方程为 ．
l y0tan45(x1) y  x1
（2）直线 的方程为 ，即 ．
y  x1

与抛物线方程联立，得 y2 4x ，
y x2 6x10 x,x x x 6
消 ，整理得 ，其两根为 1 2，且 1 2 ．
|AB| x  x  p 628
由抛物线的定义可知， 1 2 ．
所以，线段AB的长是8．
20．（2020·陕西省西安市远东一中高二期末（理））已知抛物线C的顶点为坐标原点O，对称轴为x轴，
2,1
其准线过点 .
(1)求抛物线C的方程；2 2
(2)过抛物线焦点F作直线l，使得抛物线C上恰有三个点到直线l的距离都为 ，求直线l的方程.
y2 8x x y20
【答案】(1) ；(2)
【解析】
x y2 2px
(1)由题意得，抛物线的焦点在 轴正半轴上，设抛物线C的方程为 ，
p
因为准线过点
2,1
，所以 2
2
，即 p 4 .
y2 8x
所以抛物线C的方程为 .
F2,0
(2)由题意可知，抛物线C的焦点为 .
2 2
当直线l的斜率不存在时，C上仅有两个点到l的距离为 ，不合题意；
y kx2
当直线l的斜率存在时，设直线l的方程为 ，
2 2
要满足题意，需使在含坐标原点的弧上有且只有一个点P到直线l的距离为 ，
l: y kx2
过点P的直线平行直线 且与抛物线C相切.
ykxm
设该切线方程为 ，
y2 4x k2x2 2km8xm2 0
代入 ，可得 .
2km82 4k2m2 0
由 ，得km2.
2km
2 2
由 k2 1 ，整理得 m2 4k2，
km2 k2 1 k 1
又 ，解得 ，即 .
x y20
因此，直线l方程为 .
C x2 2py(p0) F M(p,p1)
21．（2019·会泽县第一中学校高二月考（理））设抛物线 ： 的焦点为 ，是C上的点．
C
（1）求 的方程：
（2）若直线 l ： y  kx2 与 C 交于A，B两点，且 AF  BF 13 ，求 k 的值．
x2 4y
k 1
【答案】（1） （2） .
【解析】
M p,p1
C
（1）因为 是 上的点，
p2 2pp1
所以 ，
p0 p 2
因为 ，解得 ，
C x2 4y
抛物线 的方程为 .
Ax ,y  Bx ,y 
（2）设 1 1 ， 2 2 ，
y kx2

由  x2 4y 得 x2 4kx80 ，
16k2 320
x x 4k x x 8
则 1 2 ， 1 2 ，
AF  y 1 BF  y 1
由抛物线的定义知， 1 ， 2 ，
AF  BF y 1y 1kx 3kx 3
则 1 2 1 2 ，
k2x x 3kx x 9
1 2 1 2 ，
4k2 913
，
解得k 1.
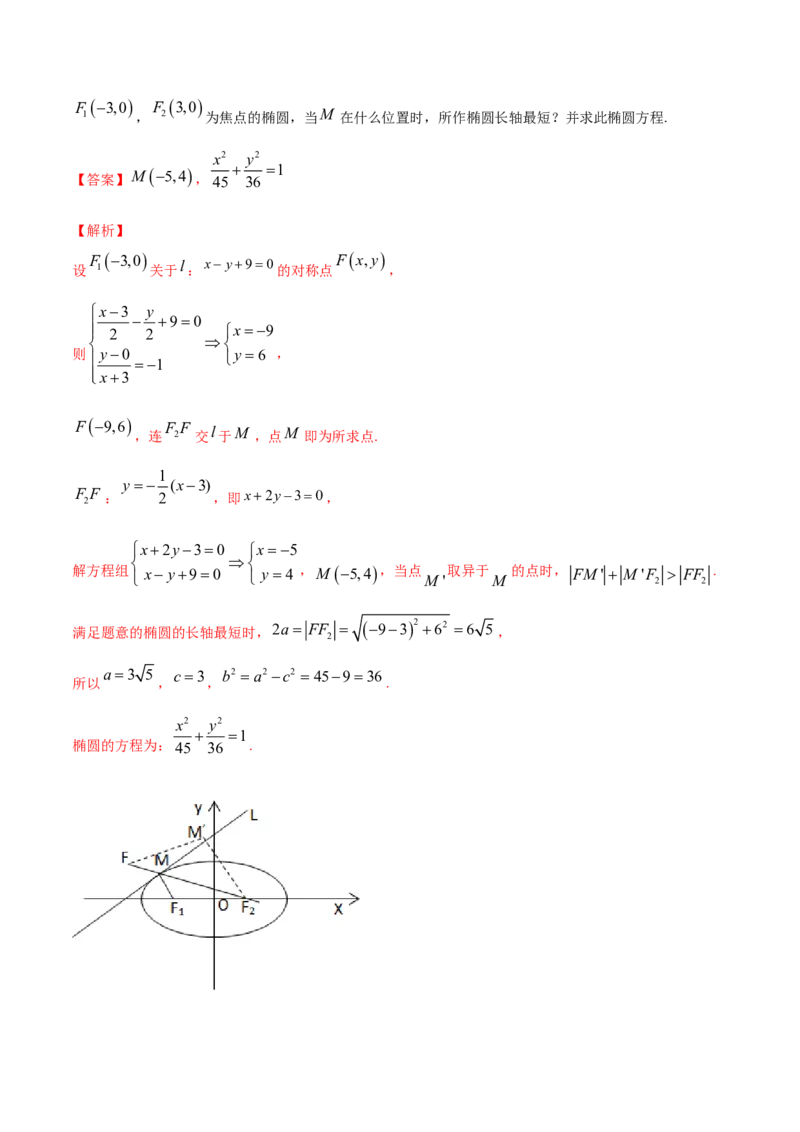
l x y90 M M
22．（2018·民勤县第一中学高二期末（文））在直线 ： 上任取一点 ，过 作以F 3,0 F 3,0
1 ， 2 为焦点的椭圆，当M 在什么位置时，所作椭圆长轴最短？并求此椭圆方程.
x2 y2
M 5,4  1
【答案】 ，45 36
【解析】
F 3,0 Fx,y
l x y90
设 1 关于 ： 的对称点 ，
x3 y
 90
  2 2 x9
 
则

y0 y 6 ，
1
x3
F9,6 F F
，连 2 交 l 于M ，点M 即为所求点.
1
y  (x3)
F F ： 2 ，即x2y30，
2
x2y30 x5
 
解方程组  x y90  y 4 ，M 5,4，当点 M ' 取异于 M 的点时， FM '  M 'F 2  FF 2 .
满足题意的椭圆的长轴最短时，2a FF  932 62 6 5 ，
2
a 3 5 c3 b2 a2 c2 45936
所以 ， ， .
x2 y2
 1
椭圆的方程为：45 36 .x2 y2
C:  1 (a b0)
23．（2019·安徽省高二期末（理））已知点O为坐标原点椭圆 a2 b2 的右焦点为
1 7
F ，离心率为2 ，点P,Q分别是椭圆C的左顶点、上顶点，△POQ的边PQ上的中线长为 2 ．
C
（1）求椭圆 的标准方程；
 
F l A、B PA、PB x2a M、N FM FN
（2）过点 的直线 交椭圆于 两点直线 分别交直线 于 两点，求 ．
x2 y2
 1
【答案】（1） 4 3 ；（2）0.
【解析】
（1）如图所示7
由题意得△POQ为直角三角形，且PQ上的中线长为 2 ，
PQ  7
所以 ．
c 1


a 2

则

 a2 b2  7 ，解得
a 2
.

 a2 b2 c2 b 3


 c1
 
x2 y2
 1
所以椭圆的标准方程为： 4 3 .
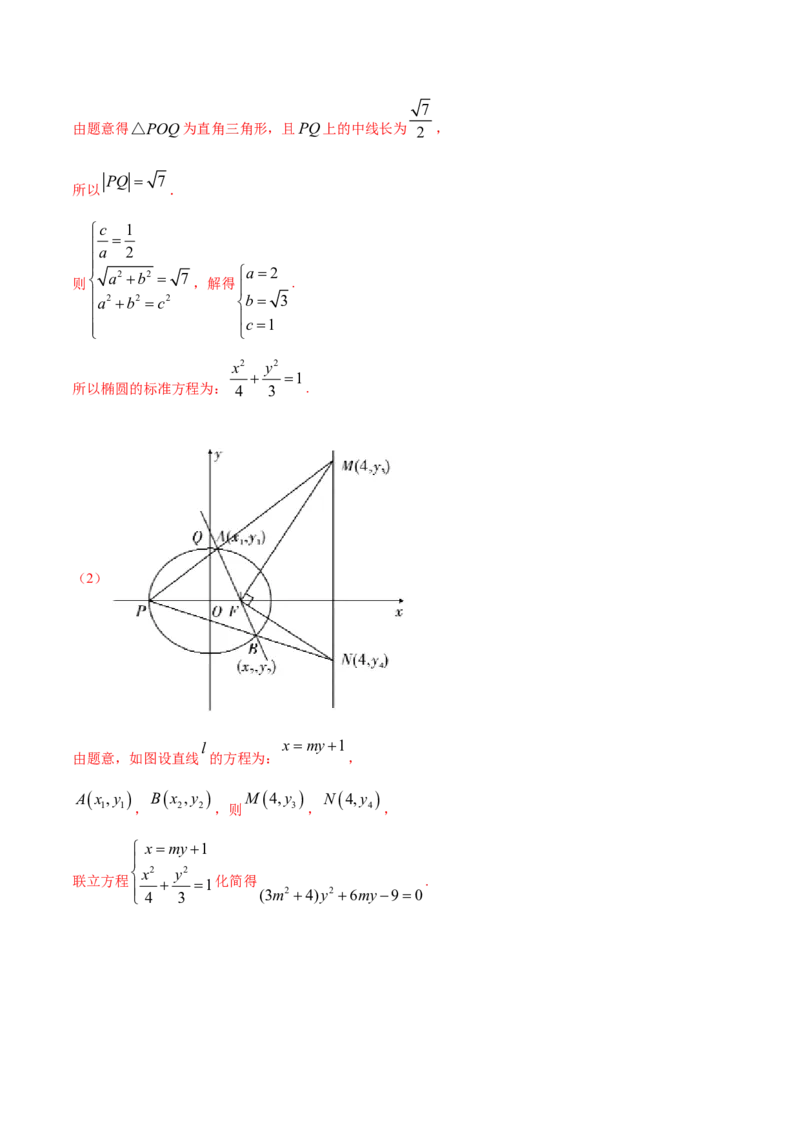
（2）
l xmy1
由题意，如图设直线 的方程为： ，
Ax ,y  Bx ,y  M 4,y  N4,y 
1 1 ， 2 2 ，则 3 ， 4 ，
 xmy1

x2 y2
联立方程  1化简得 .

 4 3 (3m2 4)y2 6my90 6m
y  y 
  1 2 3m2 4

则 9 .

y y 
 1 2 3m2 4
y 0 y 0
3  1
由P,A,M 三点共线易得42 x 2，
1
6y 6y
y  1 y  2
化简得 3 my 3，同理可得 4 my 3.
1 2
  6y 6y 36y y
FM FN (3,y ) (3,y )9 y y 9 1  2  1 2 9
3  4 3 4 my 3 my 3 m2y y 3my  y 9
1 2 1 2 1 2
9
36( )
3m2 4 369
 9 90
．
9 6m 9m2 18m2 9(3m2 4)
m2( )3m( )9
3m2 4 3m2 4