文档内容
专题3.3 解答(30道)巩固篇(期中篇)(1-3 章)
1.设全集为 ,集合 , .
(1)分别求 , ;
(2)已知 ,若 ,求实数 的取值范围构成的集合.
【答案】(1) ,( B)∪A= (2)
∁R
{a|2≤a≤8}
【解析】
(1)
(2)由题意集合 , ∴ ,∴ ,∴ .
2.已知 .
(1)求 中对应x的取值范围;
(2)若p是q的必要不充分条件,求a的取值范围.
【答案】(1) (2)
【解析】(1)因为 ,
所以
即 ,
所以
即 中对应x的取值范围为
(2)设 对应的集合为 , 对应的集合为B.
解集合q: ,得
当 时,不等式的解为 ,对应的解集为
当 时,不等式的解为 ,对应的解集为
当 时,不等式的解为 ,对应的解集为
若p是q的必要不充分条件,
当 时,满足条件;
当 时,因为 , ,
则满足 ;
当 时,因为 , ,则满足 ;
综上,实数a的取值范围为
3.设命题 实数 满足 ,其中 ,命题 实数 满足 .
(1)若 ,且 均为真命题,求实数 的取值范围;
(2)若 是 的充分不必要条件,求实数 的取值范围.
【答案】(1) (2)
【解析】
(1)由 ,
当 时, ,
即 为真命题时,
实数 的取值范围是 .
又 为真命题时,
实数 的取值范围是 ,
所以,当 均为真命题时,
有 解得 ,
所以实数 的取值范围是 .
(2) 是 的充分不必要条件,即 且 .
设 或 ,
或 ,
所以 且 ,即 .
所以实数 的取值范围是 .
4.已知a,b,c为正数,且满足abc=1.证明:
(1) ;
(2) .
【解析】
(1)
当且仅当 时取等号
,即:
(2) ,当且仅当 时取
等号又 , , (当且仅当 时等号同时成立)
又
5.已知a>0,b>0,a+b=3.
(1)求 的最小值;
(2)证明:
【答案】(1) ;(2)证明见解析
【解析】
(1) , ,且 ,
,当且仅当 即 时等号成立,
的最小值为 .(2)因为a>0,b>0,所以要证 ,需证 ,
因为 ,
所以 ,当且仅当 时等号成立.
6.已知函数
(1)解不等式 ;
(2)若 ,求证:
【答案】(1) ;(2)见解析.
【解析】
(1)原不等式化为 ,即
① 时,不等式化为 ,解得 ;
② 时,不等式化为 ,解得 , ;
③ 时,不等式化为 ,解得 , .综上可得:原不等式解集为 .
(2) ,
当且仅当 且 时取等号.又 ,
,
当且仅当 时取等号.
7.已知
(1)求证: ;
(2)求证: .
【解析】
(1)证明:因为 , ,而 ,
所以 ,(当且仅当 时取等号)
(2)因为 ,所以所以
,
当且仅当 时取等号.
8.已知函数 .
(1)当 时,求当 时,函数 的值域;
(2)解关于 的不等式 .
【答案】(1) ;(2)答案见解析.
【解析】
(1)当 时, ,此时, ,
由基本不等式可得 ,当且仅当 时,等号成立,
因此,函数 在区间 上的值域为 ;
(2) ,
令 ,得 或 .①当 ,即 时,由 ,解得 ;
②当 ,即 时,由 ,解得 ;
③当 ,即 时,由 ,解得 .
综上所述,当 时,原不等式的解集为 ;
当 时,原不等式的解集为 ;
当 时,原不等式的解集为 .
9.设函数 .
(1)当 且 时,解关于 的不等式 ;
(2)已知 ,若 的值域为 , ,求 的最小值.
【答案】(1) 或 ;(2) .
【解析】
解:(1)由 且 ,代入不等式 ,得 ,化简,得 , 或 ,
不等式的解集为 或
(2)由 的值域为 , ,可得 ,△ ,
,可得 .
, .
的最小值为 .
10.若不等式 的解集为
(1)求 值
(2)求不等式 的解集.
【答案】(1) ;(2) .
【解析】
(1)根据不等式 的解集为 ,则1,2为方程的两根,由 求解.
(2)由(1)知不等式 ,即为 ,然后利用分式不等式的解法求解.
11.设全集U=R,集合 , .
(1)当 时,求集合 ;
(2)若 ,求实数a的取值范围.
【答案】(1) ;(2) .
【解析】
(1)当 时, ,所以 ,
而 ,故 .
(2)当 时, ,符合;
当 时,因为 ,所以 ,解得 且 .
综上, .
12.已知不等式 的解集为 .
(1)若 ,求集合 ;(2)若集合 是集合 的真子集,求实数 的取值范围.
【答案】(1) ;(2) .
【解析】
(1)由题意,当 时,不等式 ,即 ,
即 ,解得 ,所以集合 .
(2)由 ,可得 ,
当 时,不等式 的解集为 .
由集合 是集合 的真子集可得 ,所以 ,
当 时,不等式 的解集为 满足题意;
当 时,不等式 的解集为 ,
由集合 是集合 的真子集,可得 ,所以 ,
综上可得: ,即实数 的取值范围为 .
13.已知函数f(x)= .
(1)求f(2)+f( ),f(3)+f( )的值;(2)求证:f(x)+f( )是定值;
(3)求f(2)+f( )+f(3)+f( )+…+f(2012)+f( )的值.
【答案】(1)1,1;(2)证明见解析;(3)2011.
【解析】
(1)∵f(x)= ,
∴f(2)+f( )= + =1,f(3)+f( )= + =1.
(2)证明:f(x)+f( )= + = + = =1.
(3)由(2)知f(x)+f( )=1,
∴f(2)+f( )=1,f(3)+f( )=1,f(4)+f( )=1,…,f(2012)+f( )=1.
∴f(2)+f( )+f(3)+f( )+…+f(2012)+f( )=2011.
14.已知函数 .(1)求 , 的值;
(2)求证: 是定值;
(3)求 的值.
【答案】(1)1;1;(2)证明见解析;(3)2011.
【解析】
解析:(1)∵ ,
∴ ,
;
(2)证明:∵ ,∴ ,∴ ,
(3)由(2)知 ,∴
∴ =2011.
15.已知函数 (a,b为常数),且方程 有两个实根
, .
(1)求函数 的解析式;
(2)设 ,解关于x的不等式: .
【答案】(1) (2)当 时, 或 ;当 时, 且
;当 时, 或 .
【解析】
(1)由题意得 ,解得 ,所以 ;
(2)原不等式可化为 ,即 .
所以当 时, 或 ;当 时, 且 ;当 时, 或.
16.(1)已知 求 的解析式;
(2)已知 是二次函数,且满足 求 的解析式.
【答案】(1) 且 ;(2) .
【解析】
(1)设 ,则 ,代入 ,
得
故 且 ;
(2)设所求的二次函数为 .
∵ 则 .
又∵
∴
即由恒等式性质,得
∴所求二次函数为
17.已知函数 .
(1)求 , 的值;
(2)当 时,求x的取值范围.
【答案】(1) , ;(2)
.
【解析】
解:(1)因为
所以
所以 ,
因为 ,所以
(2)①当 时,由 ,得 ;
②当 时,满足题意
③当 时,由 ,得
综上所述:x的取值范围是: 或 .
18.(1)已知 是一次函数,满足 ,求 的解析式.
(2)已知 ,求 的解析式.
【答案】(1) ;(2) .
【解析】
解:(1)设 ,则 ,
又因为 ,所以 , , ,
所以
(2)设 , 则
,
所以 .19.已知函数 .
(1)求函数 的定义域和值域;
(2)判断函数 在区间 上单调性,并用定义来证明所得结论.
【答案】(1)定义域 ,值域 ;(2)单调递减,证明见解析.
【解析】
(1) ,
的定义域为 ,值域 .
(2)由函数解析式得该函数在 为减函数,下面证明:
任取 ,且 ,,
, , ,
.
函数在 为减函数.
20.已知函数 .
(1)若 ,写出 的单调区间(不要求证明);(2)若对任意的 ,不等式 恒成立,求实数 的取值范
围.
【答案】(1)单调递减区间为: ,单调递增区间为: ;(2)
.
【解析】
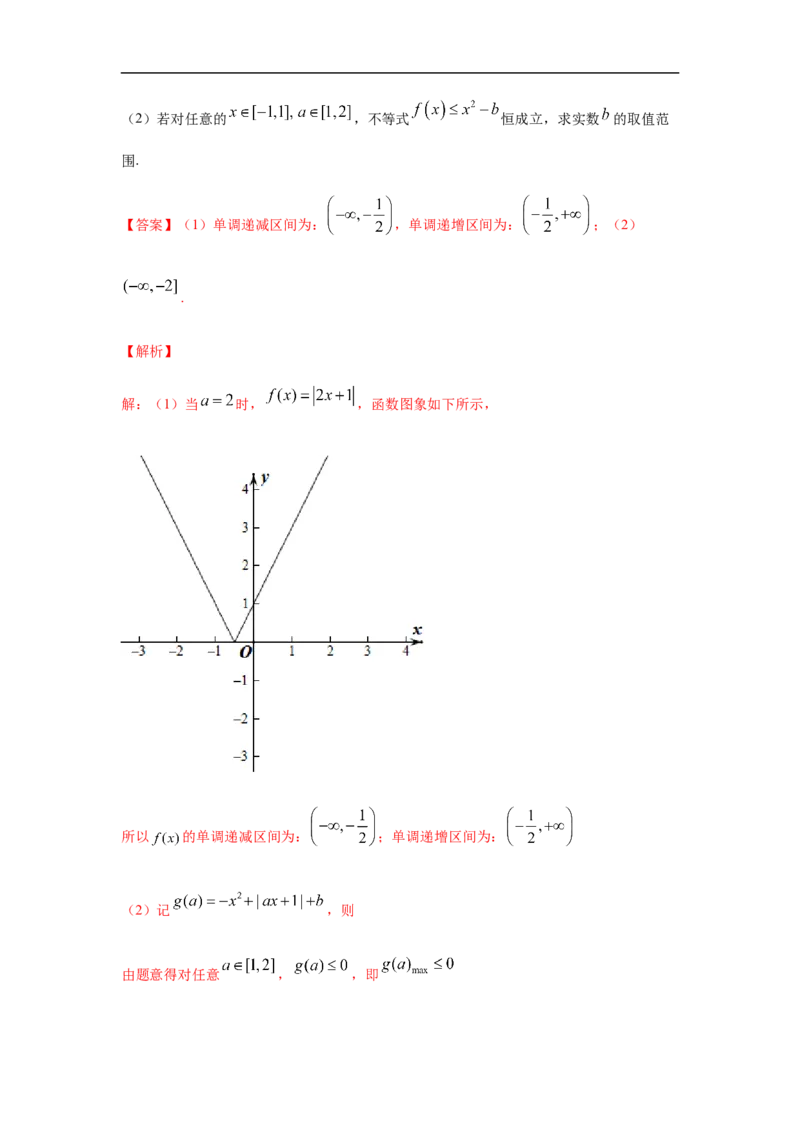
解:(1)当 时, ,函数图象如下所示,
所以 的单调递减区间为: ;单调递增区间为:
(2)记 ,则
由题意得对任意 , ,即对任意 恒成立
由(1)得 对任意 恒成立
由(2)得 对任意 恒成立
综上所述 ,即 的取值范围为
21.已知f(x)= 奇函数,且 .
(1)求实数p ,q的值.
(2)判断函数f(x)在 上的单调性,并证明.
【答案】(1)p=2,q=0(2)见解析
【解析】
解:(1)由题意可得f(﹣x)+f(x)=0,即 0,求得 q=0.
再由f(2) ,解得 p=2.
综上可得,p=2,q=0.(2)由上可得,f(x) (x ),函数f(x)在(﹣∞,﹣1)上是增函
数.
证明:设x<x<﹣1,则f(x)﹣f(x) [(x )﹣(x )] (x﹣x)(
1 2 1 2 1 2 1 2
).
由题设可得 (x﹣x)<0,x•x>1,故有f(x)﹣f(x)<0,
1 2 1 2 1 2
故函数f(x)在(﹣∞,﹣1)上是增函数.
22.定义在 上的函数 对任意 , 都有 ( 为
常数).
(1)当 时,证明 为奇函数;
(2)设 ,且 是 上的增函数,已知 ,若不等式
对任意 恒成立,求实数 的取值范围.
【答案】(1)证明见解析;(2) .
【解析】
(1)根据题意,函数 满足 ,
当 时,令 ,由 ,得 ,即 ,
令 , ,则 ,
又 ,则有 ,即 对任意 成立,
∴ 是奇函数.
(2)根据题意,∵ ,∴ ,
∴ .
又 是 上的增函数,∴ ,即 ,
分2种情况讨论:
①当 时,不等式显然成立;此时不等式的解集为 ;
②当 时,则有 ,解得 ,
综上可得,实数 的取值范围是 .
23.设函数 ,作出 的图像并讨论其性质.
【解析】
因为 ,
所以将幂函数 的图象向左平移一个长度单位后,再向上平移一个长度单位可得函数的图象,其函数图象如图:
其定义域为: ,值域为: ,函数 为非奇非偶函数,图像
关于 对称,在 上单调递增,在 上单调递减.
24.已知幂函数 在 上单调递增,函数 ;
(1)求 的值;
(2)当 时,记 、 的值域分别是 、 ,若 ,求实数 的取
值范围;
【答案】(1) 0 ; (2)
【解析】
(1) 函数 为幂函数,
则 ,解得: 或 .
当 时, 在 上单调递增,满足条件.
当 时, 在 上单调递减,不满足条件.综上所述 .
(2)由(1)可知, ,则 、 在 单调递增,
所以 在 上的值域 , 在 的值域 .
因为 ,即 ,
所以 ,即 ,所以 .
所以实数 的取值范围是 .
25.已知幂函数 在 上单调递减.
(1)求 的值并写出 的解析式;
(2)试判断是否存在 ,使得函数 在 上的值域为
?若存在,求出 的值;若不存在,请说明理由.
【答案】(1) ;(2)存在, .
【解析】
(1)因为幂函数 在 上单调递减,
所以 解得: 或 (舍去),所以 .
(2)由(1)得 ,所以 ,
假设存在 使得命题成立,则
当 时,即 , 在 单调递增,
所以 ;
当 ,即 , 显然不成立;
当 ,即 , 在 单调递减,
所以 无解;
综上所述:存在 使命题成立.
26.已知幂函数 为偶函数,在区间 上是单调增函数,
(1)求函数 的解析式;
(2)设函数 ,若 恒成立,求实数q
的取值范围.
【答案】(1) ;(2)
【解析】(1)
(2)
27.已知幂函数 的图象经过点 .
(1)求函数 的解析式;
(2)证明:函数 在 上是减函数.
【答案】(1) (2)证明见详解.
【解析】
(1)设幂函数 ,则有 ,
即 ,∴ ,
∴ .(2)证明:在 上任取 ,且 .
则 ,
因为 ,故 ,即
∴ ,
∴函数 在 上是减函数.即证.
28.已知幂函数 的图象过点 .
(1)求出函数 的解析式,判断并证明 在 上的单调性;
(2)函数 是 上的偶函数,当 时, ,求满足 时实数
的取值范围.
【答案】(1) , 在 上是增函数;证明见解析(2)
【解析】
(1)设幂函数的解析式为 ,
将点 代入解析式中得 ,
解得 ,
所以,所求幂函数的解析式为 .幂函数 在 上是增函数.
证明:任取 ,且 ,则
,
因为 , ,
所以 ,即幂函数 在 上是增函数
(2)当 时, ,
而幂函数 在 上是增函数,
所以当 时, 在 上是增函数.
又因为函数 是 上的偶函数,所以 在 上是减函数.
由 , 可得: ,
即 ,
所以满足 时实数 的取值范围为 .29.已知函数 , .
(1)若对任意 , ,不等式 恒成立,求 的取值范围.
(2)若存在 ,对任意 ,总存在唯一 ,使得
成立,求 的取值范围.
【答案】(1) 或 或 ;(2) 或 .
【解析】
(1)因为 , ,所以 ,
所以 , ,故 ,
要使对任意 , ,不等式 恒成立,只需
,
所以 ,即 .
记 ,因为 ,所以只需 ,即 ,
解得 或 或 .
故 的取值范围为 或 或 .(2)当 时, ;
当 时, ,因为 ,当且仅当
时,等号成立,所以 ,
所以函数 在 上的值域为 .
由题意知 ,
以下分三种情况讨论:
①当 ,即 时,则 ,解得 ;
②当 ,即 时,则 ,解得 ;
③当 ,即 时,则 或
,即 或 ,所以 ,或 .
综上, 的取值范围为 或 .
30.已知函数 是幂函数.
(1)求函数 的解析式;
(2)判断函数 的奇偶性,并证明你的结论;
(3)判断函数 在 上的单调性,并证明你的结论.
【答案】(1) ;(2)函数 为偶函数;(3) 在 上单调递减,证明见解
析.
【解析】
(1)因为函数 是幂函数,
则 ,
解得 ,
故 .
(2)函数 为偶函数.
证明如下:由(1)知 ,其定义域为 关于原点对称,因为对于定义域内的任意 ,都有
,
故函数 为偶函数.
(3) 在 上单调递减.
证明如下:在 上任取 , ,不妨设 ,
则
,
且 ,
,
在 上单调递减.
【点睛】
本题主要考查的是幂函数,函数的奇偶性、单调性,主要是它们定义的应用,考查学生的
计算能力,是基础题.