文档内容
专题 4.4 对数函数
1 对数函数
(1)对数函数的概念
函数y=log x(a>0 , a ≠1)叫做对数函数,其中x是自变量,定义域是(0,+∞).
a
解释
函数y=log x中系数为1,底数是不为1正实数的常数,真数为变量x.
a
(2)图像与性质
a>1 00,且
a
a≠1)的函数称为对数型函数.
4 反函数
指数函数 且 与对数函数 互为反函数.
y=ax (a>0, a≠1) y=log x(a>0 , a ≠1)
a
它们的图象关于直线y=x对称,定义域与值域相反.
比如 y=2x与y=log x互为反函数.
2一、单选题
1.函数 的单调递减区间是
A. B. C. D.
2.已知 , , ,则 的大小关系为( )
A. B.
C. D.
3.设函数 ,则使得 成立的 的取值范围为
( )
A. B.
C. D.
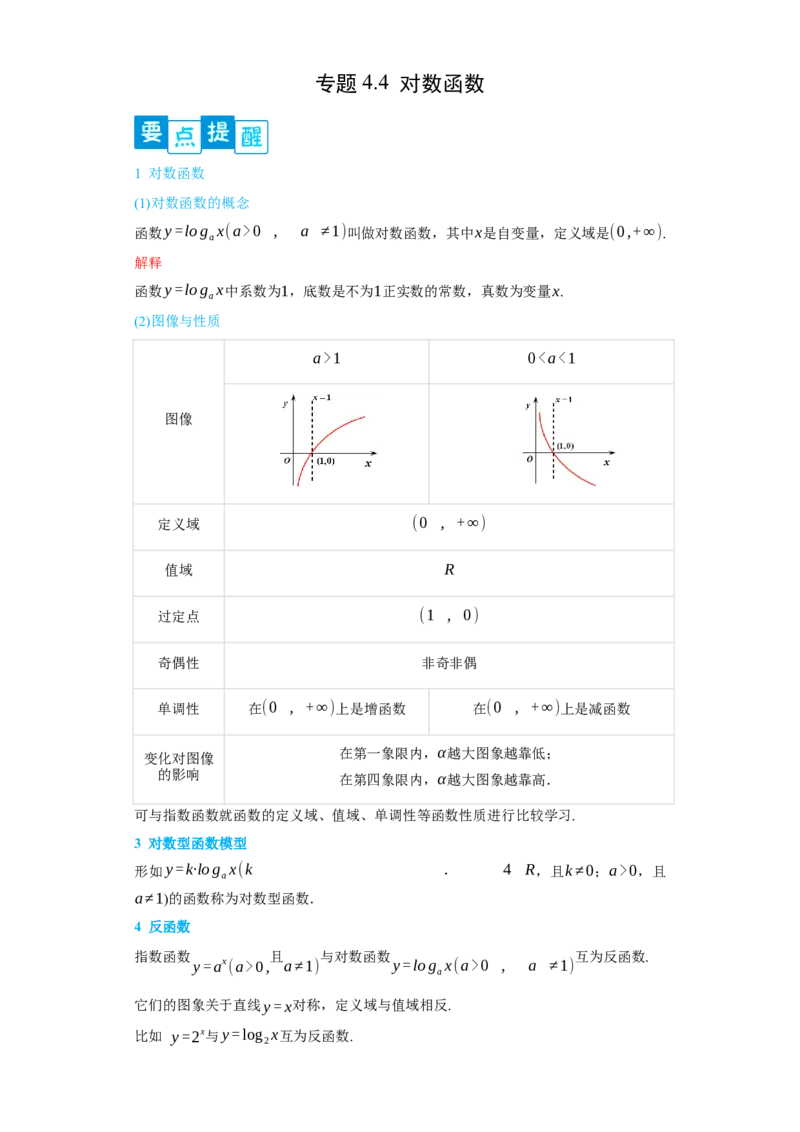
4.已知图中曲线 分别是函数 , , ,
的图像,则 的大小关系是( )A. B.
C. D.
5.已知函数 在 上单调递增,则 的取值范围是( )
A. B. C. D.
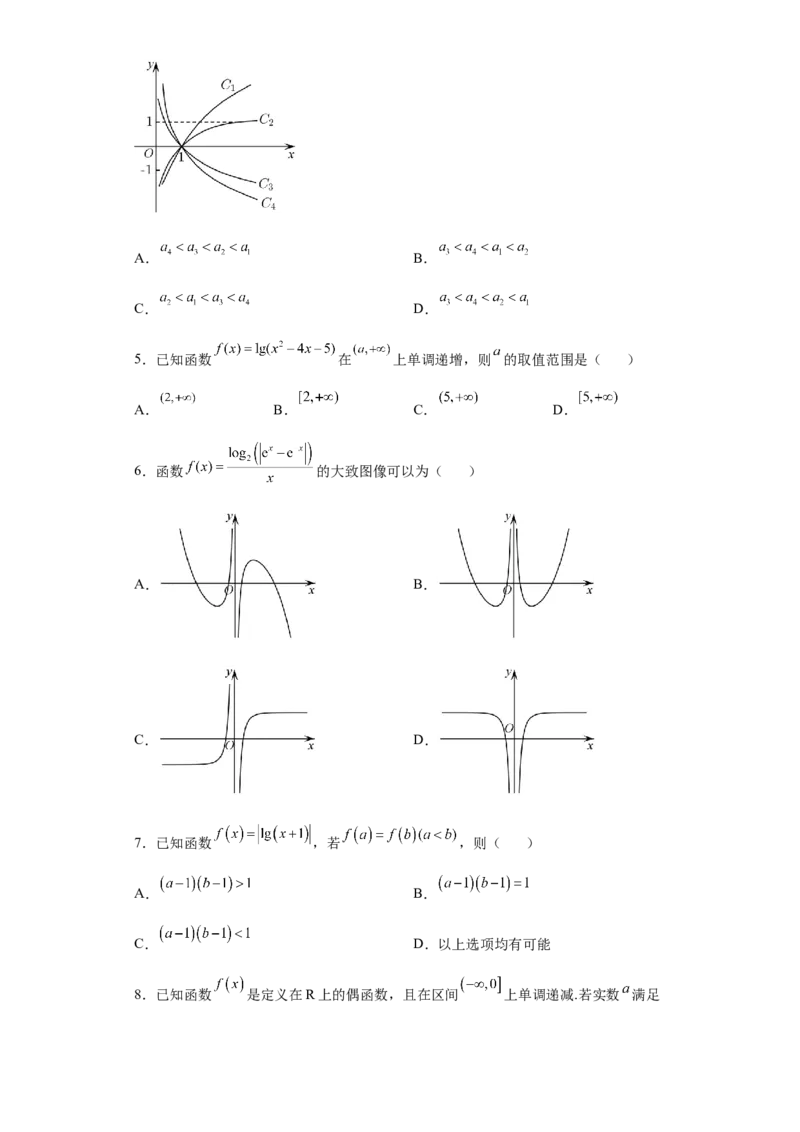
6.函数 的大致图像可以为( )
A. B.
C. D.
7.已知函数 ,若 ,则( )
A. B.
C. D.以上选项均有可能
8.已知函数 是定义在R上的偶函数,且在区间 上单调递减.若实数 满足,则 的取值范围是( )
A. B. C. D.
9.已知函数 , ,对于任意 ,存在
有 ,则实数 的取值范围是( )
A. B.
C. D.
10.在天文学中,天体的明暗程度可以用星等或亮度来描述.两颗星的星等与亮度满足
,其中星等为mk的星的亮度为Ek(k=1,2).已知太阳的星等是–
26.7,天狼星的星等是–1.45,则太阳与天狼星的亮度的比值为
A.1010.1 B.10.1 C.lg10.1 D.
11.函数 是定义在R上的偶函数,且在 单调递增,若 , ,
,则( )
A. B.
C. D.
12.已知函数 ,若不等式 恒成立,则实数a的
取值范围为( )A. B. C. D.
13.已知函数 若 存在最小值,则实数a的取值范围是( )
A. B.
C. D.
14.定义在R上的偶函数 满足对任意 ,有 ,且当
时, ,若函数 在 上至少有3个零
点,则实数 的取值范围是( )
A. B. C. D.
二、多选题
15.已知函数 ,( )
A.该函数的定义域
B.当 时,该函数的单增区间是
C.当 时,该函数的单增区间是
D.该函数的值域为R
16.已知 ,则下列结论正确的是( )
A.
B.函数 单调递增区间为
C.当 时,方程 有三个不等实根D.当且仅当 时,方程 有两个不等实根
17.已知函数 , ,则下列说法正确的是( )
A.若函数 的定义域为 ,则实数 的取值范围是
B.若函数 的值域为 ,则实数
C.若函数 在区间 上为增函数,则实数 的取值范围是
D.若 ,则不等式 的解集为
18.已知函数 ,则下列四个命题中正确命题的个数是( )
A.在 上单调递减 B. 上单调递减
C. 的图象关于直线 对称 D. 的值域为
19.中国传统文化中很多内容体现了数学的“对称美”,如图所示的太极图是由黑白
两个鱼形纹组成的图案,俗称阴阳鱼,太极图展现了一种相互转化,相对统一的和谐
美,定义:圆O的圆心在原点,若函数的图像将圆O的周长和面积同时等分成两部分,
则这个函数称为圆O的一个“太极函数”,则( )
A.对于圆O,其“太极函数”有1个
B.函数 是圆O的一个“太极函数”
C.函数 不是圆O的“太极函数”D.函数 是圆O的一个“太极函数”
三、填空题
20.函数 ( 且 )的图象恒过定点_________
21.函数 的定义域是__________.
23.设函数 ,则 的单调递增区间为_________.
24.若不等式 在 上恒成立,则实数a的取值范围为____.
25.已知 为奇函数, ,若对 、 ,
恒成立,则b的取值范围为___________.
四、解答题
26.已知函数 .
(1)判断函数 的奇偶性,并进行证明;
(2)若实数 满足 ,求实数 的取值范围.
27.已知函数 .
(1)求函数f(x)的值域;
(2)若 ,且 ,求实数m的取值范围.
28.已知函数 是 上的偶函数,且当 时, .
(1)求 的值;
(2)求函数 的表达式,并直接写出其单调区间(不需要证明);(3)若 ,求实数 的取值范围.
29.已知函数 的图象关于原点对称,其中 为常数.
(1)求 的值;
(2)当 时, 恒成立,求实数 的取值范围.
30.已知函数
(1)若m=1,求函数f(x)的定义域;
(2)若函数f(x)在区间 上是增函数,求实数m的取值范围.
31.已知函数 ),当点M(x,y)在函数g(x)的图象上运动
时,对应的点 在f(x)的图象上运动,则称g(x)是f(x)的相关函数.
(1)解关于x的不等式 ;
(2)若对任意的 ,f(x)的图象总在其相关函数图象的下方,求a的取值范围;
(3)设函数 , ,当 时,求|F(x)|的最大值.