文档内容
专题 5.1 任意角与弧度制
一、角的相关概念
1.角可以看成平面内一条射线绕着它的端点从一个位置旋转到另一个位置所成的图形.
2.角的表示:
如图,OA是角α的始边,OB是角α的终边,O是角的顶点.角α可记为“角α”或
“∠α”或简记为“α”.
3.按照角的旋转方向可将角分为如下三类:
4.相反角
如图,我们把射线OA绕端点O按不同方向旋转相同的量所成的两个角叫做互为相反
角.角α的相反角记为-α.
二、象限角
1.若角的顶点在原点,角的始边与x轴的非负半轴重合,则角的终边在第几象限,就称
这个角是第几象限角.
2.若角的终边在坐标轴上,则认为这个角不属于任何一个象限.
3.象限角的判定方法
(1)根据图象判定.依据是终边相同的角的概念,因为0°~360°之间的角的终边与坐标
系中过原点的射线可建立一一对应的关系.
(2)将角转化到0°~360°范围内.在直角坐标平面内,在0°~360°范围内没有两个角终边是相同的.
(3)nα所在象限的判断方法
确定nα终边所在的象限,先求出nα的范围,再直接转化为终边相同的角即可.
(4)所在象限的判断方法
4.已知角α所在象限,要确定角所在象限,有两种方法:
①用不等式表示出角的范围,然后对k的取值分情况讨论:被n整除;被n除余1;被
n除余2;…;被n除余n-1.从而得出结论.
②作出各个象限的从原点出发的n等分射线,它们与坐标轴把周角分成4n个区域.从
x轴非负半轴起,按逆时针方向把这4n个区域依次循环标上1,2,3,4.α的终边在第几象
限,则标号为几的区域,就是的终边所落在的区域.如此,所在的象限就可以由标号
区域所在的象限直观地看出.
三、终边相同的角
1.设α表示任意角,所有与角α终边相同的角,包括α本身构成一个集合,这个集合可
记为{β|β=□α+k·360°,k∈Z}.
2.对终边相同的角的理解
(1)终边相同的角不一定相等,但相等的角终边一定相同;
(2)k∈Z,即k为整数,这一条件不可少;
(3)终边相同的角的表示不唯一.
四、角的单位制
1.用度作为单位来度量角的单位制叫做角度制,规定1度的角等于周角的.
2.长度等于半径长的圆弧所对的□圆心角叫做1弧度的角,弧度单位用符号rad表示,
读作弧度,通常略去不写.以弧度作为单位来度量角的单位制叫做弧度制.
3.弧度数的计算
4.角度制和弧度制的比较
(1)弧度制是以“弧度”为单位来度量角的单位制,而角度制是以“度”为单位来度量
角的单位制.
(2)1弧度的角是指等于半径长的弧所对的圆心角,而 1度的角是指圆周角的的角,大
小显然不同.
(3)无论是以“弧度”还是以“度”为单位来度量角,角的大小都是一个与“半径”大
小无关的值.
(4)用“度”作为单位度量角时,“度”(即“°”)不能省略,而用“弧度”作为单位度量
角时,“弧度”二字或“rad”通常省略不写.但两者不能混用,即在同一表达式中不
能出现两种度量方法.
五、角度与弧度的换算1.角度制与弧度制的换算
2.一些特殊角的度数与弧度数的对应表
度 0° 30° 45° 60° 90° 120° 135° 150° 180°
弧度 0 π
六、扇形的弧长及面积公式
1.设扇形的半径为r,弧长为l,α(0<α<2π)为其圆心角的弧度数,n为圆心角的角度数,
则扇形的弧长:l==αr,扇形的面积:S==lr=α·r2.
一、单选题
1.与 角的终边相同的角可表示为( )
A. B.
C. D.
2.下列与角 的终边一定相同的角是( )
A. B.
C. D.
3.在0°到 范围内,与 终边相同的角为( )A. B.
C. D.
4.角 所在的象限为( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
5.已知角 ,则角 的终边落在( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
6.下列说法正确的是( )
A.终边相同的角相等 B.相等的角终边相同
C.小于 的角是锐角 D.第一象限的角是正角
7. 的角化为弧度制的结果为( )
A. B. C. D.
8.中国传统折扇有着极其深厚的文化底蕴.《乐府诗集》中《夏歌二十首》的第五首
曰:“叠扇放床上,企想远风来轻袖佛华妆,窈窕登高台.”如图所示,折扇可看作是
从一个圆面中剪下的扇形制作而成若一把折扇完全打开时圆心角为 ,扇面所在大
圆的半径为 ,所在小圆的半径为 ,那么这把折扇的扇面面积为( )
A. B. C. D.以上都不对
9.把 表示成 , 的形式,则 的值可以是( )A. B. C. D.
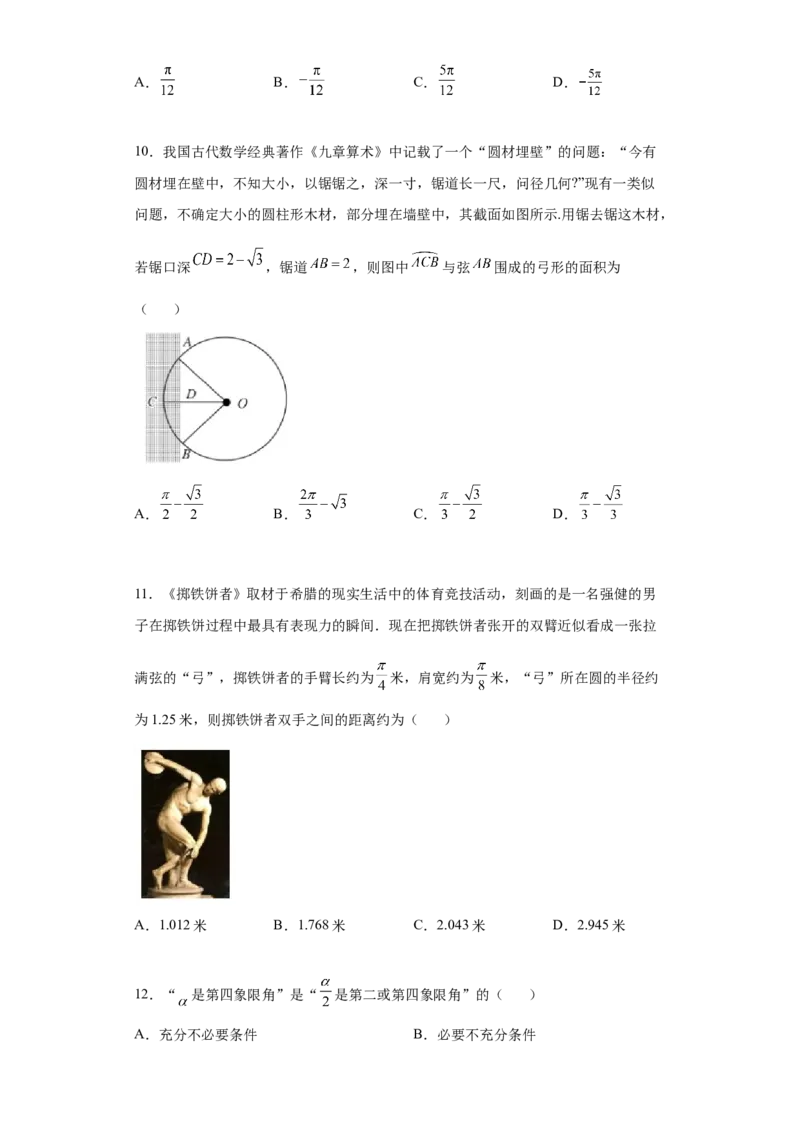
10.我国古代数学经典著作《九章算术》中记载了一个“圆材埋壁”的问题:“今有
圆材埋在壁中,不知大小,以锯锯之,深一寸,锯道长一尺,问径几何?”现有一类似
问题,不确定大小的圆柱形木材,部分埋在墙壁中,其截面如图所示.用锯去锯这木材,
若锯口深 ,锯道 ,则图中 与弦 围成的弓形的面积为
( )
A. B. C. D.
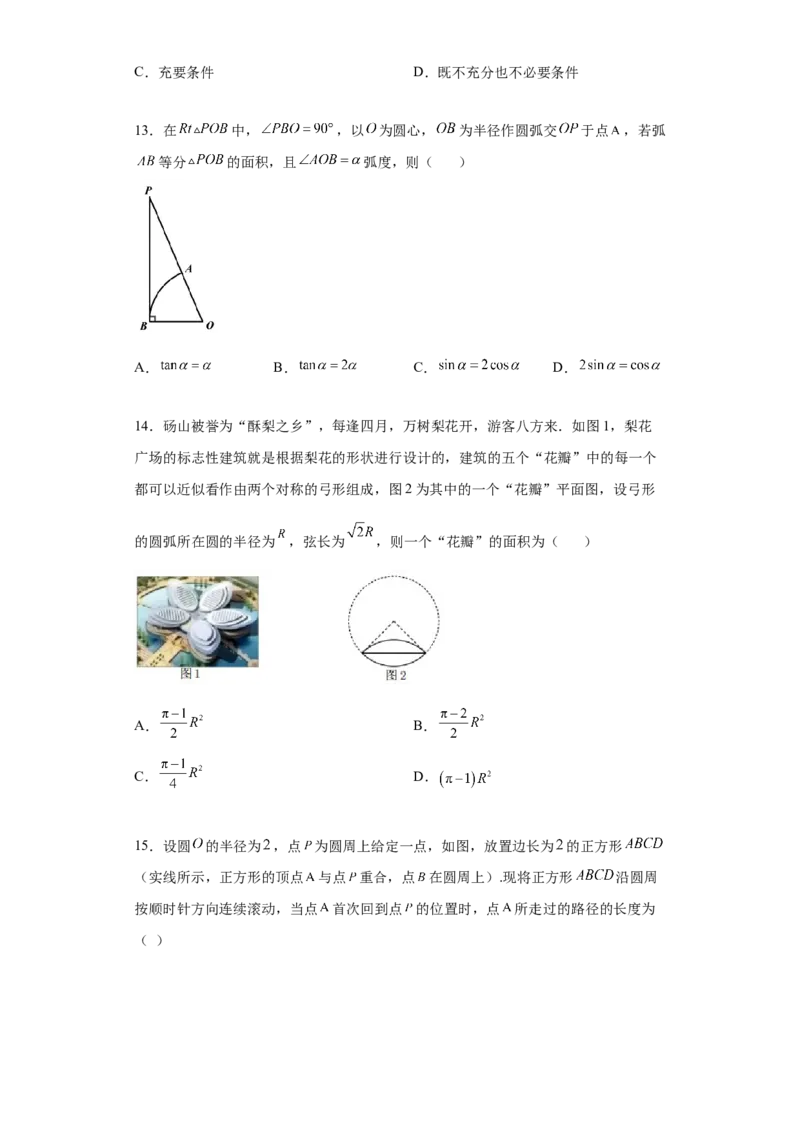
11.《掷铁饼者》取材于希腊的现实生活中的体育竞技活动,刻画的是一名强健的男
子在掷铁饼过程中最具有表现力的瞬间.现在把掷铁饼者张开的双臂近似看成一张拉
满弦的“弓”,掷铁饼者的手臂长约为 米,肩宽约为 米,“弓”所在圆的半径约
为1.25米,则掷铁饼者双手之间的距离约为( )
A.1.012米 B.1.768米 C.2.043米 D.2.945米
12.“ 是第四象限角”是“ 是第二或第四象限角”的( )
A.充分不必要条件 B.必要不充分条件C.充要条件 D.既不充分也不必要条件
13.在 中, ,以 为圆心, 为半径作圆弧交 于点 ,若弧
等分 的面积,且 弧度,则( )
A. B. C. D.
14.砀山被誉为“酥梨之乡”,每逢四月,万树梨花开,游客八方来.如图1,梨花
广场的标志性建筑就是根据梨花的形状进行设计的,建筑的五个“花瓣”中的每一个
都可以近似看作由两个对称的弓形组成,图2为其中的一个“花瓣”平面图,设弓形
的圆弧所在圆的半径为 ,弦长为 ,则一个“花瓣”的面积为( )
A. B.
C. D.
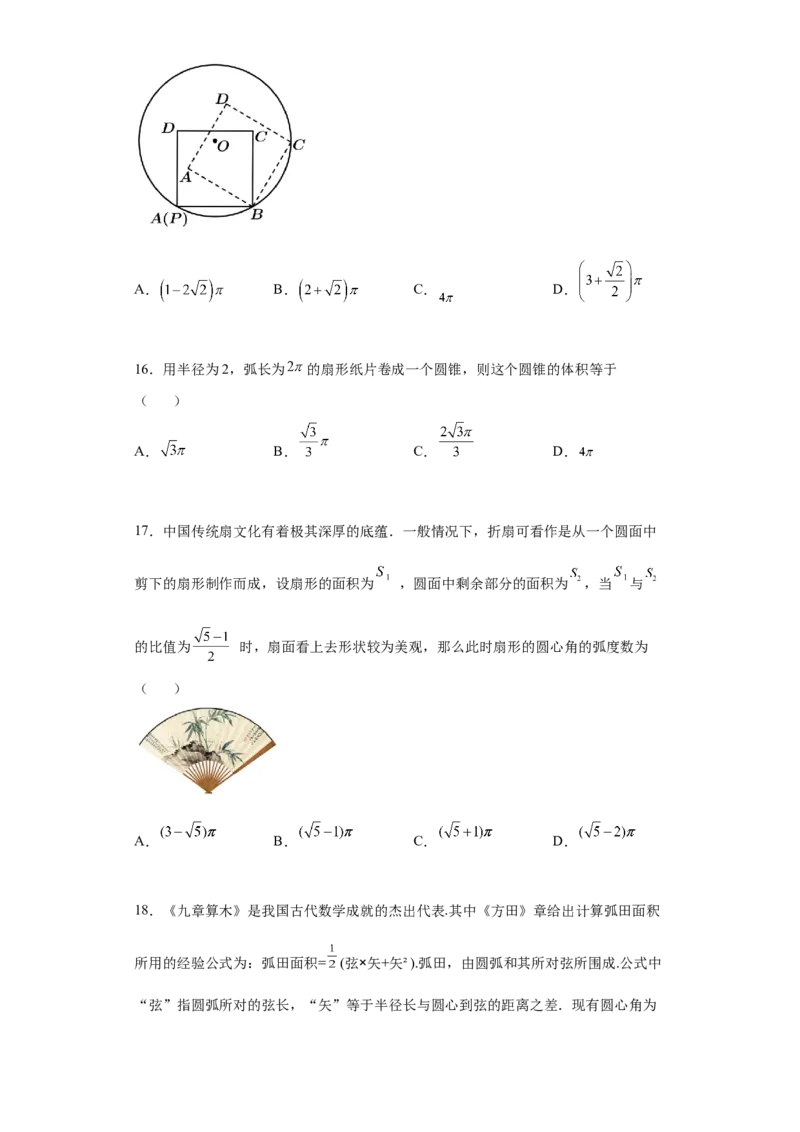
15.设圆 的半径为 ,点 为圆周上给定一点,如图,放置边长为 的正方形
(实线所示,正方形的顶点 与点 重合,点 在圆周上).现将正方形 沿圆周
按顺时针方向连续滚动,当点 首次回到点 的位置时,点 所走过的路径的长度为
( )A. B. C. D.
16.用半径为2,弧长为 的扇形纸片卷成一个圆锥,则这个圆锥的体积等于
( )
A. B. C. D.
17.中国传统扇文化有着极其深厚的底蕴.一般情况下,折扇可看作是从一个圆面中
剪下的扇形制作而成,设扇形的面积为 ,圆面中剩余部分的面积为 ,当 与
的比值为 时,扇面看上去形状较为美观,那么此时扇形的圆心角的弧度数为
( )
A. B. C. D.
18.《九章算木》是我国古代数学成就的杰出代表.其中《方田》章给出计算弧田面釈
所用的经验公式为:弧田面积= (弦×矢+矢²).弧田,由圆弧和其所对弦所围成.公式中
“弦”指圆弧所对的弦长,“矢”等于半径长与圆心到弦的距离之差.现有圆心角为,弦长等于2米的弧田.按照《九章算木》中弧田面积的经验公式竍算所得弧田面积
(单位,平方米)为
A. B. C. D.
19.将分针拨慢 分钟,则分钟转过的弧度数是( )
A. B. C. D.
20.一个圆锥的侧面展开图是圆心角为 ,弧长为 的扇形,则该圆锥的体积为
( )
A. B. C. D.
二、填空题
21.已知某圆锥的侧面积为 ,该圆锥侧面的展开图是圆心角为 的扇形,则
该圆锥的体积为______
22.《九章算术》是我国古代数学成就的杰出代表作,其中"方田"章给出了计算弧田
面积时所用的经验公式,即弧田面积 ,弧田(如图)由圆弧和其所
对弦围成,公式中“弦"指圆弧所对弦长,“矢"指圆弧顶到弦的距离(等于半径长与
圆心到弦的距离之差),现有圆心角为 ,半径为6米的弧田,按照上述经验公式计
算所得弧田面积是_________平方米.(结果保留根号)23.中国折叠扇有着深厚的文化底蕴.如图(2),在半圆 (半径为20cm)中作出两
个扇形 和 ,用扇环形 (图中阴影部分)制作折叠扇的扇面.记扇环形
的面积为 ,扇形 的面积为 ,当 时,扇形的现状较为美观,
则此时扇形 的半径为__________cm
24.“一湾如月弦初上,半壁澄波镜比明”描述的是敦煌八景之一的月牙泉.如图所示,
月牙泉由两段在同一平面内的圆弧形岸连接围成.两岸连接点间距离为 米.其中外
岸为半圆形,内岸圆弧所在圆的半径为60米.某游客绕着月牙泉的岸边步行一周,则该
游客步行的路程为_______米.
25.勒洛三角形是具有类似圆的“定宽性”的面积最小的曲线,它由德国机械工程专
家,机构运动学家勒洛首先发现,其作法是:以等边三角形每个顶点为圆心,以边长
为半径,在另两个顶点间作一段弧,三段弧围成的曲边三角形就是勒洛三角形.已知
等边三角形的边长为1,则勒洛三角形的面积是_______.
26.若扇形的周长为定值 ,则当该扇形的圆心角 ______时,扇形的面
积取得最大值,最大值为______.