2024年春季学期高一数学（答案）_2024-2025高一（7-7月题库）_2024年7月试卷_0729广西来宾市玉林市2023-2024学年高一下学期期末教学质量监测

2024 年春季期高一期末教学质量监测 数学参考答案及解析 一、单项选择题：本题共8小题，每小题5分，共40分.在每小题给出的四个选项中，只有一项是符合要 求的. 题号 1 2 3 4 5 6 7 8 答案 B C D B C A C B 1. z i(2i) 12i ∴复数z在复平面内对应的点的坐标为 1,2  ，位于第二象限．故选:B． 2. 由题意对于①，40台刚出厂的大型挖掘机被抽取的可能性一样，故为简单随机抽样，对于②，为了研 究血型与色弱的关系，说明某校800名学生被抽取的可能性要按照血型比例分层抽取，故为分层随机抽样. 故选：C. 3.大量重复试验，由表格知射击运动员射中8环以上的频率稳定在0.8，所以估计这名运动员射击一次射中 8环以上的概率为0.8，故选：D. 1 8 2 4.设航速为vnmile/h，在△ABS中，AB＝ v，BS＝8 2 nmile，∠BSA＝45°，由正弦定理，得 ＝ 2 sin30 1 v 2 ，∴v＝32nmile/h．故选：B sin45 5. 对于A，若m，则取内任意两条相交直线a,b，使得ma，mb，又m//n，则na，nb， 由线面垂直的判定定理得n，故A正确；对于B，垂直于同一条直线的 两个平面平行，故B正确； 对于C，若m//，n，如图，设m AB，平面ABCD 为平面， 1 1 1 1 m//，设平面ADDA为平面， AD n，则mn，故C错误； 1 1 1 1 对于D，由面面垂直的判定定理可得，故D正确；故选：C． 6.    a c a j sinCc j sinA，又 j 1，asinCcsinA，即  .故选：A. sinA sinC 7. 由题意可知：A1,2,3,B3,5，C{2，4，6}，因为AB3，所以事件A与B不可能是互斥， 1 1 1 又BC{2，3，4，5，6}，故B、C不对立，因为P(A) ,P(B) ，P(AB) ，所以有P(AB)P(A)P(B)， 2 3 6 1 因此事件A与B独立，故C正确；又P(BC)0，P(B)P(C) ，所以P(CB)P(B)P(C)，所以B、C不 6 独立.故选C. 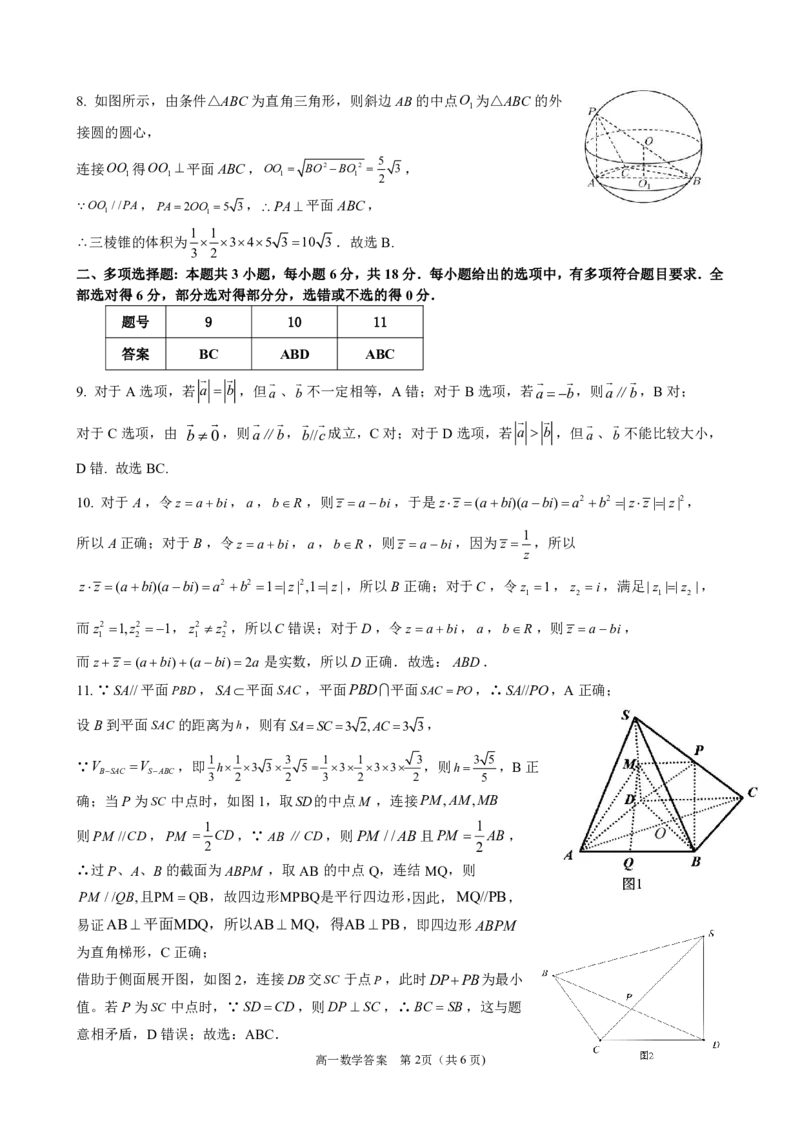高一数学答案 第1页（共6页) {#{QQABDYKEoggAAoBAAAgCUQXqCEIQkACACYgOxBAIMAAAwANABAA=}#}8. 如图所示，由条件△ABC为直角三角形，则斜边AB的中点O 为△ABC的外 1 接圆的圆心， 5 连接OO 得OO 平面ABC，OO  BO2BO2  3， 1 1 1 1 2 OO //PA，PA2OO 5 3，PA平面ABC， 1 1 1 1 三棱锥的体积为  345 310 3．故选B. 3 2 二、多项选择题: 本题共3小题，每小题6分，共18分．每小题给出的选项中，有多项符合题目要求．全 部选对得6分，部分选对得部分分，选错或不选的得0分． 题号 9 10 11 答案 BC ABD ABC         9. 对于A选项，若 a  b ，但 a 、 b 不一定相等，A错；对于B选项，若ab，则a∥b，B对；           对于C选项，由 b0，则a∥b，b//c成立，C对；对于D选项，若 a  b ，但 a 、 b 不能比较大小， D错. 故选BC. 10. 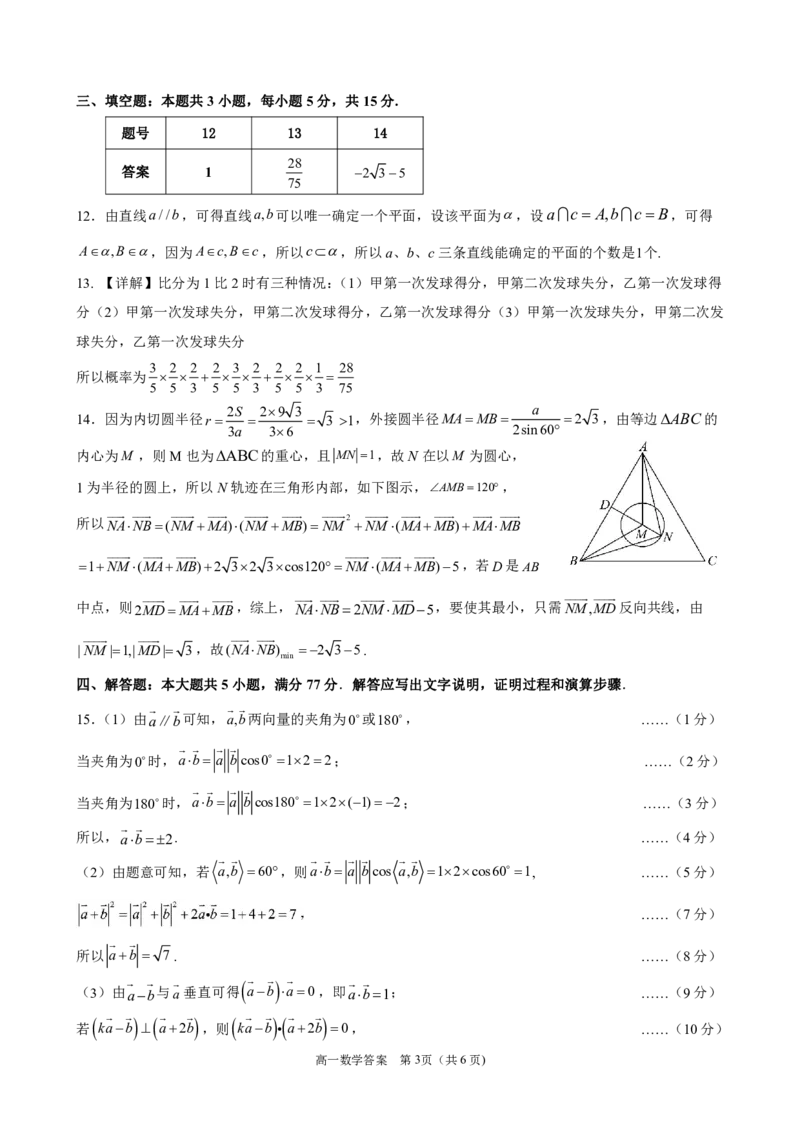对于A，令zabi，a，bR，则z abi，于是zz (abi)(abi)a2 b2 |zz ||z|2， 1 所以A正确；对于B，令zabi，a，bR，则z abi，因为z  ，所以 z zz (abi)(abi)a2 b2 1|z|2,1|z|，所以B正确；对于C，令z 1，z i，满足|z ||z |， 1 2 1 2 而z2 1,z2 1，z2 z2，所以C 错误；对于D，令zabi，a，bR，则z abi， 1 2 1 2 而zz (abi)(abi)2a 是实数，所以D正确．故选：ABD． 11.∵SA//平面PBD，SA平面SAC，平面PBD平面SACPO，∴SA//PO，A正确； 设B到平面SAC的距离为h，则有SASC3 2,AC3 3， 1 1 3 1 1 3 3 5 ∵V V ，即 h 3 3 5  3 33 ，则h ，B正 BSAC SABC 3 2 2 3 2 2 5 确；当P为SC 中点时，如图1，取SD的中点M ，连接PM,AM,MB 1 1 则PM //CD，PM  CD，∵AB∥CD，则PM //AB且PM  AB ， 2 2 ∴过P、A、B的截面为ABPM ，取AB的中点Q，连结MQ，则 PM //QB,且PMQB，故四边形MPBQ是平行四边形，因此，MQ//PB， 易证AB平面MDQ，所以ABMQ，得ABPB，即四边形ABPM 为直角梯形，C正确； 借助于侧面展开图，如图2，连接DB交SC 于点P，此时DPPB为最小 值。若P为SC 中点时，∵SDCD，则DPSC，∴BC SB，这与题 意相矛盾，D错误；故选：ABC． 高一数学答案 第2页（共6页) {#{QQABDYKEoggAAoBAAAgCUQXqCEIQkACACYgOxBAIMAAAwANABAA=}#}三、填空题：本题共3小题，每小题5分，共15分. 题号 12 13 14 28 答案 1 2 35 75 12．由直线a//b，可得直线a,b可以唯一确定一个平面，设该平面为，设ac A,bc B，可得 A,B，因为Ac,Bc，所以c，所以a、b、c三条直线能确定的平面的个数是1个. 13. 【详解】比分为1比2时有三种情况：（1）甲第一次发球得分，甲第二次发球失分，乙第一次发球得 分（2）甲第一次发球失分，甲第二次发球得分，乙第一次发球得分（3）甲第一次发球失分，甲第二次发 球失分，乙第一次发球失分 3 2 2 2 3 2 2 2 1 28 所以概率为          5 5 3 5 5 3 5 5 3 75 2S 29 3 a 14．因为内切圆半径r   3 1，外接圆半径MAMB 2 3，由等边ABC的 3a 36 2sin60 内心为M ，则M也为ABC的重心，且 MN 1，故N 在以M 为圆心， 1为半径的圆上，所以N轨迹在三角形内部，如下图示，AMB120，             所以NANB(NM MA)(NM MB)NM 2 NM(MAMB)MAMB       1NM(MAMB)2 32 3cos120NM(MAMB)5，若D是AB          中点，则 2MDMAMB ，综上，NANB2NMMD5，要使其最小，只需NM,MD反向共线，由     |NM |1,|MD| 3，故(NANB) 2 35. min 四、解答题：本大题共5小题，满分77分．解答应写出文字说明，证明过程和演算步骤．     15．（1）由a∥b可知，a,b两向量的夹角为0或180， ……（1分）     当夹角为0时，ab a bcos0 122； ……（2分）     当夹角为180时，ab a bcos180 12(1)2； ……（3分）   所以，ab2. ……（4分）         （2）由题意可知，若 a,b 60，则ab a bcos a,b 12cos60 1, ……（5分） ……（7分）   所以 ab  7. ……（8分）           （3）由 ab 与a垂直可得 ab a0，即ab1； ……（9分）                 若 kab  a2b ，则 kab  a2b 0， ……（10分） 高一数学答案 第3页（共6页) {#{QQABDYKEoggAAoBAAAgCUQXqCEIQkACACYgOxBAIMAAAwANABAA=}#}即 ，得3k90， ……（12分）         所以k 3,当k 3时， kab  a2b . ……（13分） b2c2a2 bc 1 16．（1）由b2c2a2 bc，cosA   ， ……（4分，列公式得2分，结果得2分） 2bc 2bc 2 由A0,π， ……（5分） π A ； ……（6分） 3 （2）sinC2sinB，由正弦定理得c2b①， ……（8分） 又b2c24bc，②， 联立 ①② ……（10分） 2 3 4 3 解得b ,c ， ……（12分） 3 3 1 1 2 3 4 3 3 2 3 S  bcsin A     . 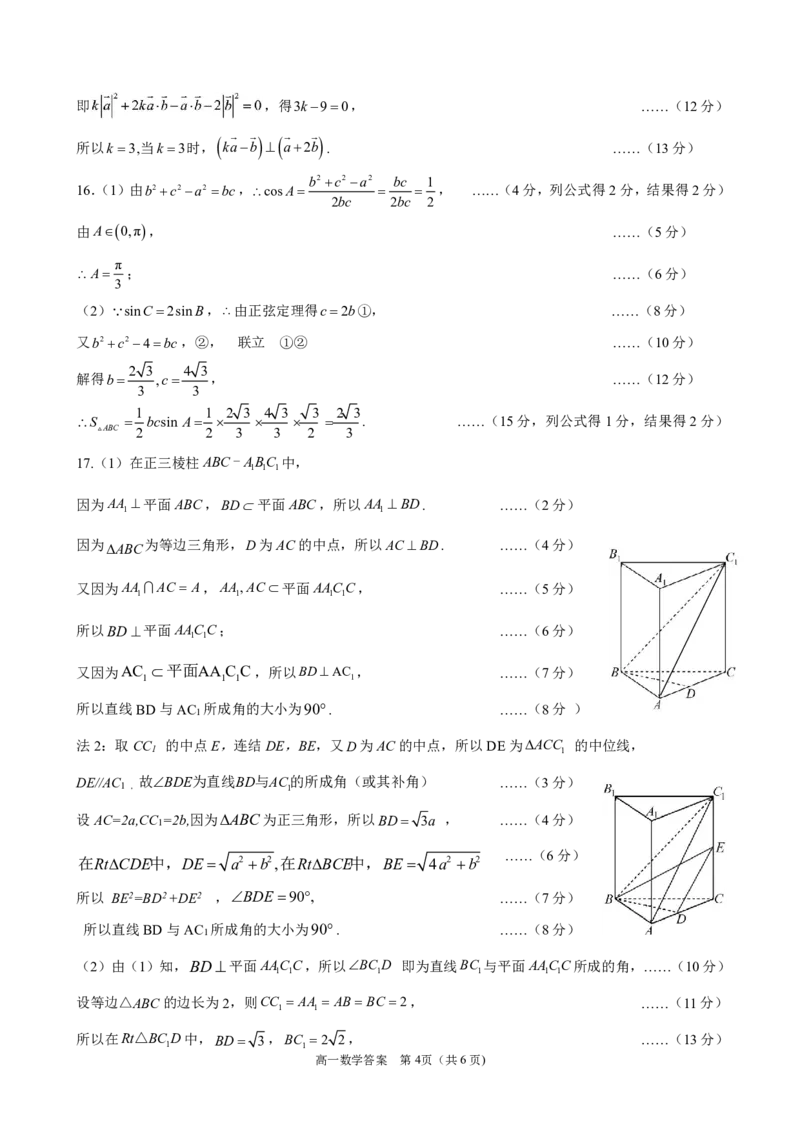……（15分，列公式得1分，结果得2分） ABC 2 2 3 3 2 3 17.（1）在正三棱柱ABC-ABC 中， 1 1 1 因为AA 平面ABC，BD平面ABC，所以AA BD. ……（2分） 1 1 因为 ABC 为等边三角形，D为AC的中点，所以ACBD. ……（4分） 又因为AA AC  A，AA,AC 平面AACC， ……（5分） 1 1 1 1 所以BD平面AACC； ……（6分） 1 1 又因为AC 平面AA CC，所以BDAC ， ……（7分） 1 1 1 1 所以直线BD与AC 所成角的大小为90. ……（8分 ） 1 法2：取CC 的中点E，连结DE，BE，又D为AC的中点，所以DE为ACC 的中位线， 1 1 DE//AC 故BDE为直线BD与AC的所成角（或其补角） ……（3分） 1 ， 1 设AC=2a,CC =2b,因为ABC为正三角形，所以BD 3a ， ……（4分） 1 ……（6分） 在RtCDE中，DE  a2 b2,在RtBCE中，BE  4a2 b2 所以 BE2=BD2+DE2 ，BDE 90, ……（7分） 所以直线BD与AC 所成角的大小为90. ……（8分） 1 （2）由（1）知，BD平面AACC，所以BC D 即为直线BC 与平面AACC所成的角，……（10分） 1 1 1 1 1 1 设等边△ABC的边长为2，则CC  AA  ABBC 2， ……（11分） 1 1 所以在Rt△BCD中，BD 3，BC 2 2， ……（13分） 1 1 高一数学答案 第4页（共6页) {#{QQABDYKEoggAAoBAAAgCUQXqCEIQkACACYgOxBAIMAAAwANABAA=}#}BD 3 6 所以sinBCD   . ……（14分） 1 BC 2 2 4 1 6 即直线BC 与平面AACC所成的角的正弦值为 . ……（15分） 1 1 1 4 另解（2）如果用法2证明（1），解答如下： 在正三棱柱ABC-ABC 中，因为AA 平面ABC，BD平面ABC，所以AA BD. 1 1 1 1 1 因为 ABC 为等边三角形，D为AC的中点，所以ACBD. ……（10分） 又因为AA AC  A，AA,AC 平面AACC， 1 1 1 1 所以BD平面AACC；所以BC D 即为直线BC 与平面AACC所成的角， ……（12分） 1 1 1 1 1 1 设等边ABC的边长为2，则CC  AA  ABBC 2， 1 1 所以在Rt△BCD中，BD 3，BC 2 2， ……（13分） 1 1 BD 3 6 所以sinBCD   . 1 BC 2 2 4 1 6 即直线BC 与平面AACC所成的角的正弦值为 . ……（14分） 1 1 1 4 18．（1）设这m人的平均年龄为x，则 x22.50.0527.50.3532.50.337.50.242.50.132.25（岁）.……（3分，列对式子得1分，结 果得2分） ……（3分） 设第80百分位数为a，分数低于35分占0.05+0.35+0.3=0.7<0.8, 分数低于40分占0.05+0.35+0.3+0.2=0.9＞0.8，故a（35，40）， ……（4分） 所以0.7(a35)0.040.8，解得a37.5. ……（6分） 0.80.7 或者35+ 5=37.5 0.90.7 （2）（i）由题意得，第四组应抽取4人，记为A，B，C，甲，第五组抽取2人，记为D，乙， ……（7分） 对应的样本空间为： {(A,B),(A,C),(A,甲),(A,乙),(A,D),(B,C),(B,甲),(B,乙),(B,D),(C,甲),(C,乙), (C,D),(甲,乙),(甲,D),(乙,D)}，共15个样本点. ……（9分） 设事件M “甲、乙两人至少一人被选上”，则 M {(A,甲),(A,乙),(B,甲),(B,乙),(C,甲),(C,乙),(甲,乙),(甲,D),(乙,D)}，共有9个样本点 .……（11分） 高一数学答案 第5页（共6页) {#{QQABDYKEoggAAoBAAAgCUQXqCEIQkACACYgOxBAIMAAAwANABAA=}#}n(M) 3 所以，P(M)  . ……（12分） n() 5 （ii）设第四组、第五组的宣传使者的年龄的平均数分别为x ，x ，方差分别为s2，s2， 4 5 4 5 5 则x 37，x 43，s2  ，s2 1， 4 5 4 2 5 设第四组和第五组所有宣传使者的年龄平均数为 z ，方差为s2. 4x 2x 则z 4 5 39， ……（14分） 6   1   2   2 s2  6 4  s2 4  x 4 z  2  s2 5  x 5 z  10 ， ……（16分） 因此，第四组和第五组所有宣传使者的年龄方差为10， 据此，可估计这m人中年龄在35至45岁的所有人的年龄方差约为10. ……（17分） 19. （1）由BB底面圆O，且l 底面圆O，∴BBl， ……（2分） 又因为ABl，AB,BB平面ABB，ABBBB ……（4分） ∴l 平面ABB ……（5分） 而AB平面ABB，则ABl。 ……（6分） （2）①因为ABl且ABl，所以BAB为平面与底面二面角的平面角 ……（8分） π 又因为AB AA2，所以BAB . ……（9分） 4 过点M做MF垂直于直线l垂足为F，连接NF， 由MN 底面O，则MN l,又MF l，且MN MF M，l 平面MNF，所以FNl π 则NFM BAB ，MN FM ， ……（12分） 4 作ME垂直于直径AB垂足为E，四边形AFME为矩形，AE FM ∵AB2，则底面圆O半径OA1   又因为A  M x，所以AOM  x,当x  0,  时， OEcosx，AE OAOE 1cosx ，  2 FM 1cosx， ……（14分）   当x  ，  时，OE cos(x)cosx,AE OAOE 1cosx,FM 1cosx,  2  同理，当x(,2)时，也有FM 1cosx ……（15分） 又∵MN  FM ，∴MN 1cosx，∴y1cosx，x 0,2π ……（17分） （ 注：若没有给出x的取值范围扣1分,范围是两边都闭或一开一闭都可以。） 高一数学答案 第6页（共6页) {#{QQABDYKEoggAAoBAAAgCUQXqCEIQkACACYgOxBAIMAAAwANABAA=}#}