文档内容
专题 1.2 集合间的基本关系【九大题型】
【人教A版(2019)】
【题型1 子集、真子集的概念】..............................................................................................................................2
【题型2 有限集合子集、真子集的确定】..............................................................................................................2
【题型3 判断两个集合是否相等】..........................................................................................................................3
【题型4 根据两个集合相等求参数】......................................................................................................................4
【题型5 空集的判断及应用】..................................................................................................................................4
【题型6 Venn图表示集合的关系】.........................................................................................................................4
【题型7 集合间关系的判断】..................................................................................................................................6
【题型8 利用集合间的关系求参数】......................................................................................................................6
【题型9 集合间关系中的新定义问题】..................................................................................................................7
【知识点1 子集与真子集】
1.子集的概念
一般地,对于两个集合A,B,如果集合A中任意一个
定义
元素都是集合B中的元素,称集合A为集合B的子集
记法 记作 (或 ),读作“A包含于B”(或“B包
与读法
含A”)
图示
或
(1)任何一个集合是它本身的子集,即 ;
结论
(2)对于集合A,B,C,若 ,且 ,则
2.真子集的概念
学科网(北京)股份有限公司如果集合 ,但存在元素 ,且 ,我们
定义
称集合A是集合B的真子集
记法 记作 (或 )
图示
(1) 且 ,则 ;
结论
(2) ,且 ,则
【注】(1)“A是B的子集”的含义:集合A中的任何一个元素都是集合B的元素,即有任意x∈A能
推出x∈B.
(2)不能把“A B”理解为“A是B中部分元素组成的集合”,因为集合A可能是空集,也可能是集合
B.
(3)特殊情形:如果集合A中存在着不是集合B中的元素,那么集合A不包含于B,或集合B不包含集
合A.
(4)对于集合A,B,C,若A B,B C,则A C;任何集合都不是它本身的真子集.
(5)若A B,且A≠B,则A B.
【题型1 子集、真子集的概念】
【例1】(2023·高一课时练习)已知A是非空集合,则下列关系不正确的是( )
A.
A⊆A
B.A⊂A C.
∅⊆A
D.∅⊂A
≠ ≠
【变式1-1】(2023·高一课时练习)集合A={x∣0≤x<4,且x∈N}的真子集的个数是( )
A.16 B.15 C.8 D.7
【变式1-2】(2023·全国·高一假期作业)已知集合A={0,1,2,3},则含有元素0的A的子集个数是( )
A.2 B.4
C.6 D.8
【变式1-3】(2023·河南·统考模拟预测)已知集合 ,则集合 的所有非空真子集的
A={x∈N|−22}={y|y>2} D.{1,2}={2,1}
【变式3-2】(2023·全国·高一假期作业)已知集合 和
M={(x,y)|x+ y<0,xy>0}
,那么( )
P={(x,y)|x<0,y<0}
A.P⊆M B.M⊆P C.M=P D.M≠P
学科网(北京)股份有限公司{ 1 }
【变式3-3】(2023秋·四川眉山·高一校考期末)若集合A= x|x= (2k+1),k∈Z ,
9
{ 4 1 }
B= x|x= k± ,k∈Z ,则集合A,B之间的关系表示最准确的为( )
9 9
A.A⊆B B.B⊆A C.A=B D.A与B互不包含
【题型4 根据两个集合相等求参数】
【例4】(2023春·湖南长沙·高二校考期末)已知实数集合 若 ,则
A={1,a,b},B={a2,a,ab}, A=B
a+b=( )
A.−1 B.0 C.1 D.2
【变式4-1】(2023·广西河池·校联考模拟预测)设集合M={5,x2},N={5x,5}.若M=N,则实数x的值
组成的集合为( )
A.{5} B.{1} C.{0,5} D.{0,1}
【变式4-2】(2023·江西·校联考模拟预测)已知集合 , ,若 ,则
A={1,a,b} B={a2,a,ab} A=B
a2023+b2022=( )
A.−1 B.0 C.1 D.2
【变式4-3】(2023·全国·高三专题练习)已知集合A={x|x2+px+q=x},B={x|(x-1)2+p(x-1)+q=x+
3},当A={2}时,集合B=( )
A.{1} B.{1,2}
C.{2,5} D.{1,5}
【题型5 空集的判断及应用】
【例5】(2023·全国·高一假期作业)下列集合中为∅的是( )
A.{0} B.{∅}
C.{x|x2+4=0} D.{x|x+1≤2x}
【变式5-1】(2023·全国·高一假期作业)下列四个集合中,是空集的是( )
A. B.
{x|x+3=3} {(x,y)|y2=−x2,x,y∈R}
C. D.
{x|x2≤0} {x|x2−x+1=0,x∈R}
【变式5-2】(2023·全国·高一假期作业)已知六个关系式①
∅∈{∅}
;②∅⊂{∅};③{0}⊃∅;④
≠ ≠
学科网(北京)股份有限公司0∉∅;⑤∅={0};⑥∅≠{∅},它们中关系表达正确的个数为( )
A.3 B.4 C.5 D.6
【变式5-3】(2023春·宁夏银川·高二校考期中)下列各式中:①{0}∈{0,1,2};②{0,1,2}⊆{2,1,0};
③∅⊆{0,1,2};④∅={0};⑤{0,1}={(0,1)};⑥0={0}.正确的个数是( )
A.1 B.2 C.3 D.4
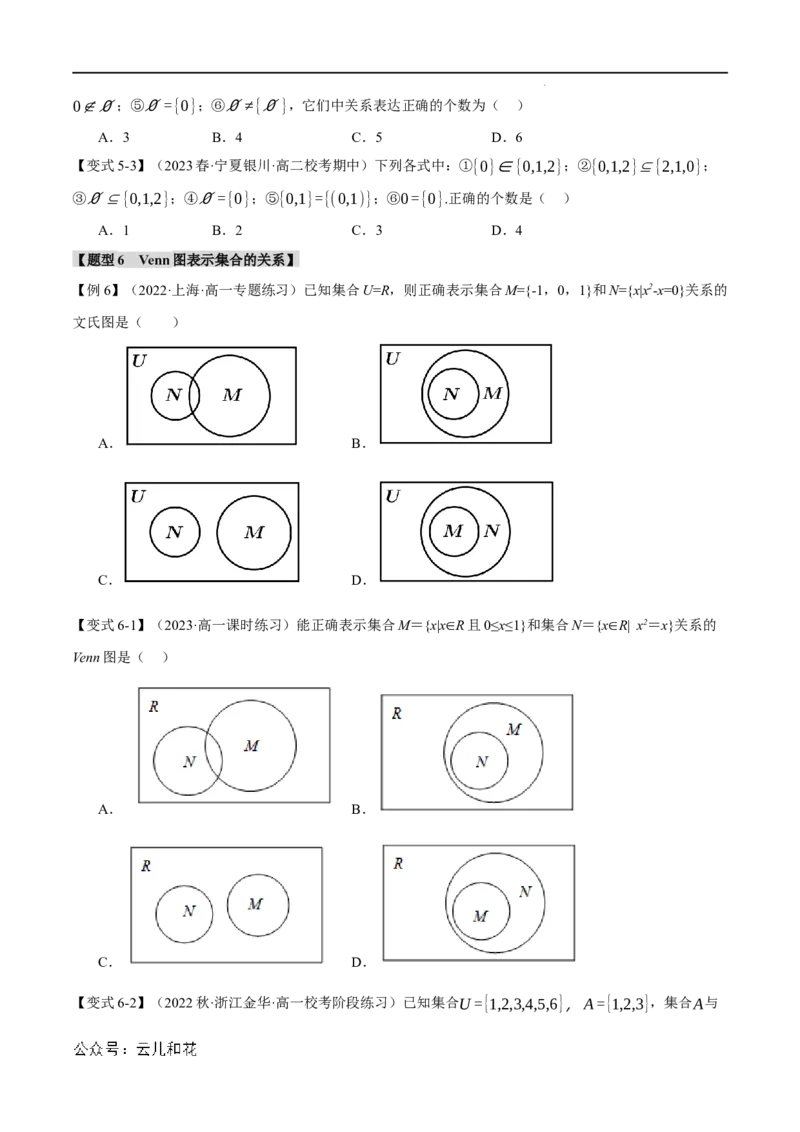
【题型6 Venn图表示集合的关系】
【例6】(2022·上海·高一专题练习)已知集合U=R,则正确表示集合M={-1,0,1}和N={x|x2-x=0}关系的
文氏图是( )
A. B.
C. D.
【变式6-1】(2023·高一课时练习)能正确表示集合M={x|x∈R且0≤x≤1}和集合N={x∈R| x2=x}关系的
Venn图是( )
A. B.
C. D.
【变式6-2】(2022秋·浙江金华·高一校考阶段练习)已知集合U={1,2,3,4,5,6},A={1,2,3},集合A与
学科网(北京)股份有限公司B的关系如图所示,则集合B可能是( )
A.{2,4,5} B.{1,2,5} C.{1,6} D.{1,3}
【变式6-3】(2022秋·高一课时练习)已知集合U、S、T、F的关系如图所示,则下列关系正确的是(
)
①S∈U;②F⊆T;③S⊆T;④S⊆F;⑤S∈F;⑥F⊆U.
A.①③ B.②③
C.③④ D.③⑥
【知识点3 集合间关系的性质】
集合间关系的性质:
(1)任何一个集合都是它本身的子集,即A A.
(2)对于集合A,B,C,
①若A B,且B C,则A C;
②若A B,B=C,则A C.
(3)若A B,A≠B,则A B.
【题型7 集合间关系的判断】
【例7】(2023·江苏·高一假期作业)集合A={(x,y)|y=|x|},集合B={(x,y)|y>0,x∈R},则下列
说法正确的是( )
A.A⊆B
B.B⊆A
C.B=A
D.集合A,B间没有包含关系
【变式7-1】(2023春·北京·高三校考开学考试)集合A={−2,−1,0},若A⊆B,则集合B可以是( )
A.{−1} B.{−1,1} C.{−1,0,1} D.{−2,−1,0,1}
kπ+π π kπ π
【变式7-2】(2023·全国·高三专题练习)设集合M={x|x= − ,k∈Z},N={x|x= + ,
2 4 4 2
学科网(北京)股份有限公司k∈Z},则( )
A.M=N B.M⊊N C.M⊆N D.M⊋N
k
【变式7-3】(2023春·江西新余·高一校考阶段练习)若A={x|x= +1,k∈Z},
6
k 1 2k 1
B={x|x= + ,k∈Z},C={x|x= + ,k∈Z},则这三个集合间的关系是( )
3 2 3 2
A.A⊆B⊆C B.A⊆C⊆B C.C⊆B⊆A D.C⊆A⊆B
【题型8 利用集合间的关系求参数】
【例8】(2023·全国·高三专题练习)设集合A={0,−a},B={1,a−2,2a−2},若A⊆B,则a=( )
2
A.2 B.1 C. D.−1
3
【变式8-1】(2023·四川成都·校考模拟预测)已知集合 ,若 ,
A={x∈N||x|<2},B={x∣ax−1=0} B A
则实数a=( )
1 1
A. 或1 B.0或1 C.1 D.
2 2
【变式8-2】(2023·全国·高三专题练习)设a,b∈R,A={1,a},B={−1,−b},若A⊆B,则a−b=
( )
A.−1 B.−2 C.2 D.0
【变式8-3】(2023春·河北保定·高三校考阶段练习)已知集合A={x|x≥11},B=¿,若A⊆B,则实数
m的取值范围是( ).
A.(−∞,4] B.(−∞,4) C.(−∞,22) D.(−∞,22]
【题型9 集合间关系中的新定义问题】
【例9】(2022·全国·高三专题练习)定义集合A★B={x∣x=ab,a∈A,b∈B},设A={2,3},B={1,2},
则集合A★B的非空真子集的个数为( )
A.12 B.14 C.15 D.16
【变式9-1】(2022·江苏·高一专题练习)对于两个非空集合A,B,定义集合A−B=¿且x∉B},若
M={1,2,3,4,5},N={0,2,3,6,7},则集合N-M的真子集个数为( )
A.5 B.6 C.7 D.8
【变式9-2】(2022·高一单元测试)定义A∗B={Z|Z=xy+1,x∈A,y∈B},设集合A={0,1},
集合B={1,2,3},则A*B集合的真子集的个数是( )
A.14 B.15 C.16 D.17
学科网(北京)股份有限公司【变式9-3】(2022秋·安徽合肥·高一校考阶段练习)对于任意两个正整数m,n ,定义某种运算 ,法
则如下:当m,n都是正奇数时,m n=m+n ;当m,n不全为正奇数时,m n=mn,则在此定义下,
集合M={(a,b)|a b=16,a∈N∗,b∈N∗}的真子集的个数是( )
A.27−1 B.211−1 C.213−1 D.214−1
学科网(北京)股份有限公司