文档内容
专题 1.6 集合与常用逻辑用语全章六类必考压轴题
【人教A版(2019)】
考点1 交、并、补集的混合运算
1.(2023·河北衡水·衡水市校考三模)已知全集I={x∈N∣x≤10},集合M={1,2,3},N={2,4,6,8,10},
则∁ (M∪N)=( )
I
A.{5,7,9} B.{1,2,3,4,6,8,10}
C.{0,5,7,9} D.{0,1,2,3,4,6,8,10}
2.(2023·江苏连云港·统考模拟预测)已知全集 , ,
U=A∪B={x∈N|0≤x≤7} A∩(∁ B)={1,3,5,7}
U
则集合B=( )
A.{0,2,4,6} B.{2,4,6} C.{0,2,4} D.{2,4}
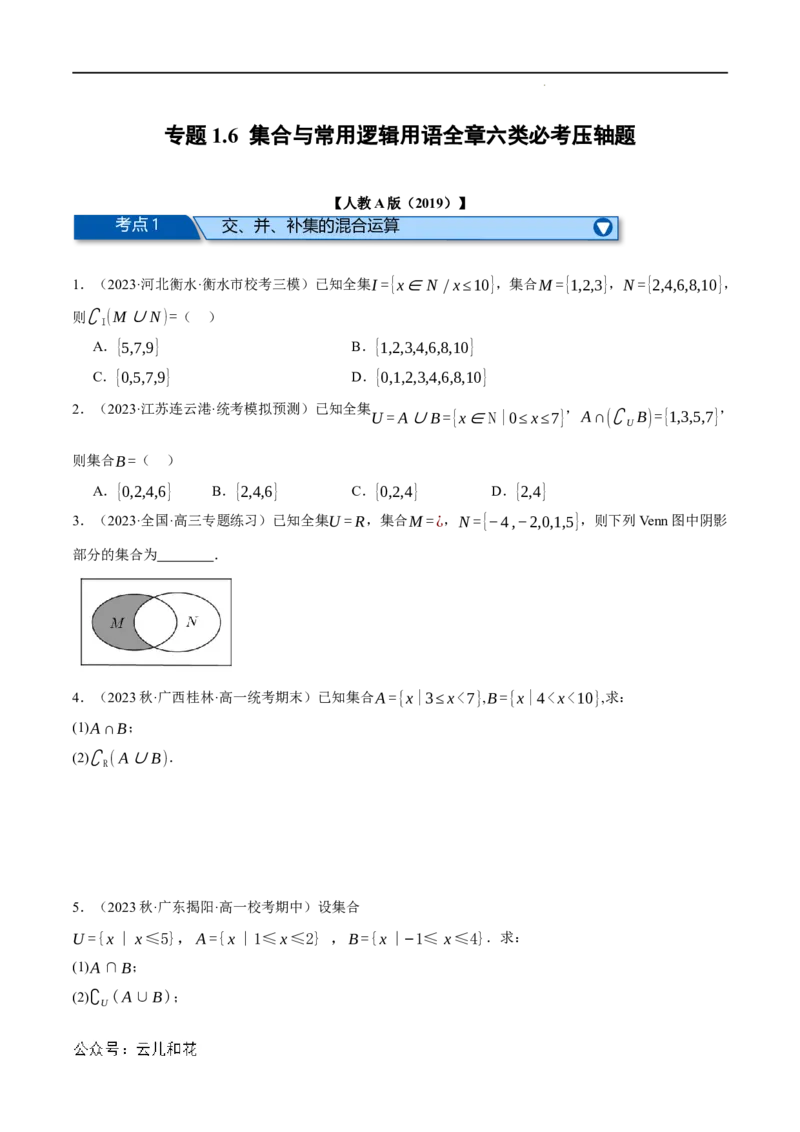
3.(2023·全国·高三专题练习)已知全集U=R,集合M=¿,N={−4,−2,0,1,5},则下列Venn图中阴影
部分的集合为 .
4.(2023秋·广西桂林·高一统考期末)已知集合A={x|3≤x<7},B={x|41},B={x∣x≤a−1},若
A∪B=R,则实数a的取值范围为( )
A.(−∞,1] B.(−∞,2] C.[1,+∞) D.[2,+∞)
2.(2023·全国·高三专题练习)设集合 或 , ,若 ,则 的取值范围是
A=¿ x≥4} B=¿ (∁ A)∩B≠∅ a
R
( )
A.a<2 B.a>2 C.a≤4 D.a≥4
3.(2022秋·高一课时练习)已知 , ,且 ,
A={x∣x2+px−6=0} B={x∣x2+qx+2=0} A∩(∁ B)={2}
R
则p+q的值等于_____.
4.(2023·全国·高一假期作业)设集合A={x|x2-3x+2=0},B={x|x2+2(a+1)x+a2-5=0}.
(1)若A∩B={2},求实数a的值;
(2)若A∪B=A,求实数a的取值范围;
(3)若U=R,A∩(
∁
B)=A,求实数a的取值范围.
U
5.(2023秋·山东德州·高一校考阶段练习)已知A=¿,B=¿.
(1)若a=1,求A∩(∁ B);
Z
(2)从① ;② ;③ 这三个条件中任选一个,补充在下面横线上,
A∪(∁ B)=R A∩B=B B∩(∁ A)=∅
R R
并进行解答.
问题:若__________,求实数a的所有取值构成的集合C.
注:如果选择多个条件分别解答,按第一个解答计分.
学科网(北京)股份有限公司考点4 集合与充分、必要条件的综合应用
1.(2023春·吉林长春·高二校考期中)已知集合 ,集合 .
A={x|1−m≤x≤1+m} B={x|x2−8x−20≤0}
(1)若m=5,求A∩B,A∪B;
(2)若x∈B是x∈A的必要条件,求实数m的取值范围.
2.(2023·全国·高一专题练习)设U=R,已知集合A={x|−2≤x≤5},B={x|m+1≤x≤2m−1}.
(1)当4∈B时,求实数m的范围;
(2)设p:x∈A;q:x∈B,若p是q的必要不充分条件,求实数m的范围.
3.(2023秋·安徽芜湖·高一校考期末)设全集是 ,集合 .
R A={x|a0 B.a≥0 C.a≤0 D.a≤1
2.(2023春·四川宜宾·高二校考期末)已知命题p:∃x∈R,x2+2x+2−a=0为真命题,则实数a的值
不能是( )
A.1 B.2 C.3 D.−3
3.(2023·高一课时练习)已知命题p:∀x∈[1,2],x2−a≥0,命题q:∀x∈R,x2+2ax+2−a≠0,
若命题p和¬q都是真命题,则实数a的取值范围是 .
4.(2023·高一课时练习)命题p:“∀x∈[1,2],x2−a≥0”,命题q:“∃x∈R,
x2+3x+2−a=0”,若p和q中至少有一个是假命题,求实数a的取值范围.
5.(2023春·江苏南京·高二校考期末)已知命题p存在实数x∈R,使x2−ax+1≤0成立.
(1)若命题p为真命题,求实数a的取值范围;
(2)若命题q:任意实数x∈[1,2],使x2−ax+1≤0恒成立,如果命题“p或q”为假命题,求实数a的取
值范围.
学科网(北京)股份有限公司考点6 集合与命题的综合应用
1.(2023·全国·高一假期作业)已知集合 , ,且 .若命
A={x|−2≤x≤5} B={x|m+1≤x≤2m−1} B≠∅
题p:“∀x∈B,x∈A”是真命题,求m的取值范围;
2.(2023·全国·高一假期作业)已知集合A=¿ ,B=¿,且B≠∅.
(1)若命题p:“∀x∈B,x∈A”是真命题,求实数m的取值范围;
(2)若命题q:“∃x∈A,x∈B”是真命题,求实数m的取值范围.
3.(2023春·福建南平·高二校考期中)已知集合A=¿
(1)若B⊆A,求实数m的取值范围.
(2)命题q:“∃x∈A,使得x∈B”是真命题,求实数m的取值范围.
4.(2022秋·江苏扬州·高一统考阶段练习)已知命题p:∃x∈R,x2−6x+a2=0,当命题p为真命题时,
实数a的取值集合为A.
(1)求集合A;
(2)设集合B=¿,若x∈A是x∈B的必要不充分条件,求实数m的取值范围.
学科网(北京)股份有限公司5.(2023秋·重庆九龙坡·高一统考期末)设全集U=R,集合A=¿,非空集合B=¿,其中a∈R.
(1)当a=4时,求A∩∁ B;
R
(2)若命题“∃x∈B,x∈∁ A”是真命题,求实数a的取值范围.
U
学科网(北京)股份有限公司