文档内容
专题 14 预备知识十四:函数的应用(一)
1、会利用已知函数模型解决实际问题(一次函数、二次函数、分段函数模型)
2、能建立函数模型解决实际问题
3、运用函数思想理解和处理现实生活和社会中的简单问题
知识点一:常见几类函数模型
函数模型 函数解析式
一次函数模型 ( , 为常数, )
二次函数模型 ( , , 为常数, )
分段函数模型
幂函数模型 ( , , 为常数, )
知识点二:对钩函数(耐克函数)
1、对钩函数(一般模型):对勾函数是一种类似于反比例函数的一般双曲函数,又被称为“双勾函数”、
“勾函数”、“对号函数”、“双飞燕函数”;所谓的对勾函数,是形如: ( ,
)的函数;
①定义域: ;
② 是奇函数,图象关于原点对称;
学科网(北京)股份有限公司 学科网(北京)股份有限公司③ 在 , 上单调递减;在 , 上单调递增;
④当 时, ;当 时, ;
2、(高频考试模型)特别的,对钩函数的简易形式: ( )其图象如图:
①定义域: ;
② ( )是奇函数,图象关于原点对称;
③ 在 , 上单调递减;在 , 上单调递增;
④当 时, ;当 时, ;
对点特训一:一次函数模型
典型例题
例题1.(23-24高一上·四川眉山·开学考试)冰墩墩(Bing Dwen Dwen)、雪容融(Shuey Rhon Rhon)
分别是2022年北京冬奥会、冬残奥会的吉祥物.冬奥会来临之际,冰墩墩、雪容融玩偶畅销全国.小雅
在某网店选中两种玩偶,决定从该网店进货并销售,第一次小雅用1400元购进了冰墩墩玩偶15个和雪容
融玩偶5个,已知购进1个冰墩墩玩偶和1个雪容融玩偶共需136元,销售时每个冰墩墩玩偶可获利28元,
每个雪容融玩偶可获利20元.
(1)求两种玩偶的进货价分别是多少?
学科网(北京)股份有限公司 学科网(北京)股份有限公司(2)第二次小雅进货时,网店规定冰墩墩玩偶的进货数量不得超过雪容融玩偶进货数量的1.5倍.小雅计划
购进两种玩偶共40个,应如何设计进货方案才能获得最大利润,最大利润是多少元?
例题2.(23-24高一上·吉林长春·期中)某种商品在30天内每件的销售价格P(元)与时间t(t∈N )(天)的函
+
数关系用如图的两条线段表示,该商品在30天内日销售量Q(件)与时间t(t∈N )(天)之间的关系如下表:
+
t/天 5 10 20 30
Q/件 35 30 20 10
(1)根据提供的图象(如图),写出该商品每件的销售价格P与时间t的函数关系式;
(2)根据上表提供的数据,写出日销售量Q与时间t的一个函数关系式;
(3)求该商品日销售金额的最大值,并指出日销售金额最大的一天是30天中的第几天(日销售金额=每件的
销售价格×日销售量).
精练
1.(2024高一·全国·专题练习)商店出售茶壶和茶杯,茶壶每个定价为20元,茶杯每个定价为5元,该
商店现推出两种优惠办法:
(1)买一个茶壶赠送一个茶杯.
(2)按购买总价的92%付款.
某顾客需购茶壶4个,茶杯若干个(不小于茶壶数),若购买茶杯数为x(个),付款数为y(元),试用
两种优惠办法分别建立y与x之间的函数解析式,并指出如果顾客需买茶杯40个应选择哪种优惠办法.
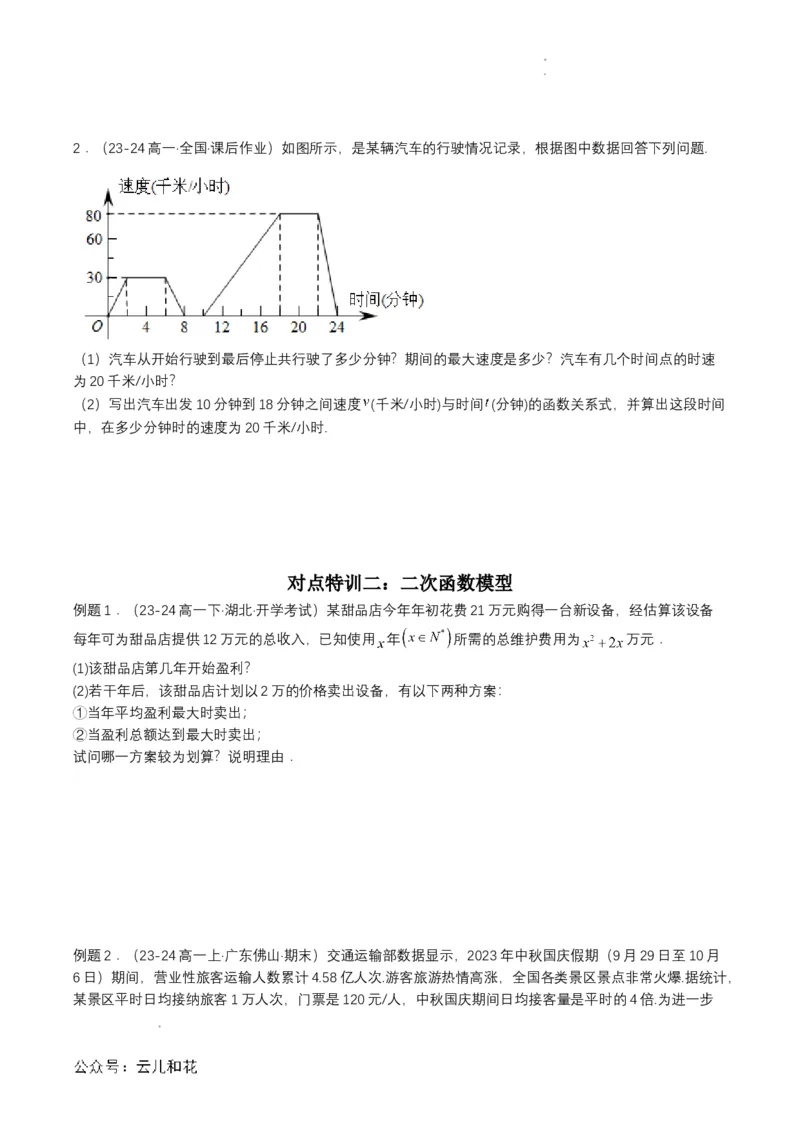
学科网(北京)股份有限公司 学科网(北京)股份有限公司2.(23-24高一·全国·课后作业)如图所示,是某辆汽车的行驶情况记录,根据图中数据回答下列问题.
(1)汽车从开始行驶到最后停止共行驶了多少分钟?期间的最大速度是多少?汽车有几个时间点的时速
为20千米/小时?
(2)写出汽车出发10分钟到18分钟之间速度 (千米/小时)与时间 (分钟)的函数关系式,并算出这段时间
中,在多少分钟时的速度为20千米/小时.
对点特训二:二次函数模型
例题1.(23-24高一下·湖北·开学考试)某甜品店今年年初花费21万元购得一台新设备,经估算该设备
每年可为甜品店提供12万元的总收入,已知使用 年 所需的总维护费用为 万元.
(1)该甜品店第几年开始盈利?
(2)若干年后,该甜品店计划以2万的价格卖出设备,有以下两种方案:
①当年平均盈利最大时卖出;
②当盈利总额达到最大时卖出;
试问哪一方案较为划算?说明理由.
例题2.(23-24高一上·广东佛山·期末)交通运输部数据显示,2023年中秋国庆假期(9月29日至10月
6日)期间,营业性旅客运输人数累计4.58亿人次.游客旅游热情高涨,全国各类景区景点非常火爆.据统计,
某景区平时日均接纳旅客1万人次,门票是120元/人,中秋国庆期间日均接客量是平时的4倍.为进一步
学科网(北京)股份有限公司 学科网(北京)股份有限公司提升中秋国庆期间的旅游门票营业额,该景区作了深度的市场调查,发现当门票每便宜10元时,旅游日
均人数可增加m万人(便宜幅度是10元一档,但优惠后的最终门票价格不低于80元).
(1)当 时,要使该景区降价后的门票日均营业额不低于495万元,则该景区可以如何确定门票价格?
(2)当m在区间 上变化时,总能使得门票日均营业额不低于520万元,则该景区应如何确定门票价
格?
精练
1.(23-24高一上·广东佛山·阶段练习)某商场销售 型商品,已知该商品的进价是每件3元,且销售单
价与日均销售量的关系如表所示:
销售单价(元) 4 5 6 7 8 9 10
日 均 销 售 量
400 360 320 280 240 200 160
(件)
请根据以上数据分析,此商品如何定价(单位:元/件),该商品的日均销售利润最大?并求日均销售利润
的最大值.
2.(23-24高一上·河北石家庄·期末)据国家气象局消息,今年各地均出现了极端高温天气.漫漫暑期,
某制冷杯成了畅销商品.某企业生产制冷杯每月的成本(单位:万元)由两部分构成:①固定成才(与生
产产品的数量无关): 万元;②生产所需材料成本: 万元, (单位:万套)为每月生产产
品的套数.
(1)该企业每月产量 为何值时,平均每万套的成本最低?一万套的最低成本为多少?
(2)若每月生产 万套产品,每万套售价为: 万元,假设每套产品都能够售出,则该企业应如何制
定计划,才能确保该制冷杯每月的利润不低于 万元?
学科网(北京)股份有限公司 学科网(北京)股份有限公司对点特训三:分式函数模型(基本不等式工具)
典型例题
例题1.(23-24高二下·北京房山·期中)某公园为了美化游园环境,计划修建一个如图所示的总面积为
的矩形花园.图中阴影部分是宽度为1m的小路,中间 , , 三个矩形区域将种植牡丹、郁金香、
月季(其中 , 区域的形状、大小完全相同).设矩形花园的一条边长为 ,鲜花种植的总面积为 .
(1)用含有 的代数式表示 ;
(2)当 的值为多少时,才能使鲜花种植的总面积最大?
例题2.(23-24高二下·全国·期中)为了在夏季降温和冬季供暖时减少能源损耗,房屋的屋顶和外墙需要
建造隔热层.某幢建筑物要建造可使用32年的隔热层,每厘米厚的隔热层建造成本为8万元.该建筑物每
年的能源消耗费用C(单位:万元)与隔热层厚度 (单位; )满足关系: ,设
为隔热层建造费用与32年的能源消耗费用之和.
(1)求 的表达式;
(2)隔热层修建多厚时,总费用 达到最小,并求最小值.
学科网(北京)股份有限公司 学科网(北京)股份有限公司精练
1.(2024高一·全国·专题练习)通过技术创新,某公司的汽车特种玻璃已进入欧洲市场. 2021年,该种玻
璃售价为25欧元/平方米,销售量为80万平方米,销售收入为2000万欧元.
(1)据市场调查,若售价每提高1欧元/平方米,则销售量将减少2万平方米;要使销售收入不低于2000万
欧元,试问:该种玻璃的售价最多提高到多少欧元/平方米?
(2)为提高年销售量,增加市场份额,公司将在2022年对该种玻璃实施二次技术创新和营销策略改革:提
高价格到 欧元/平方米(其中 ),其中投入 万欧元作为技术创新费用,投入500万欧元
作为固定宣传费用,投入 万欧元作为浮动宣传费用,试问:该种玻璃的销售量 (单位/万平方米)至
少达到多少时,才可能使2022年的销售收入不低于2021年销售收入与2022年投入之和?并求出此时的
售价.
2.(23-24高一上·江苏无锡·阶段练习)某厂家拟在2023年举行促销活动,经调查测算,该产品的年销售
量(即该厂的年产量) 万件与年促销费用 万元满足 (其中 为常数),如果不搞促
销活动,则该产品的年销售量只能是1万件.已知2023年生产该产品的固定投入为8万元,每生产1万件
该产品需要再投入16万元,厂家将每件产品的销售价格定为每件产品年平均成本的1.5倍(产品成本包括
固定投入和再投入两部分资金).
(1)求常数 的值,并将2023年该产品的利润 万元表示为年促销费用 万元的函数;
(2)该厂家的促销费用投入多少万元时,厂家的利润最大?最大利润为多少万元?
对点特训四:分段函数模型
典型例题
学科网(北京)股份有限公司 学科网(北京)股份有限公司例题1.(23-24高一下·四川泸州·阶段练习)丽水市某革命老区因地制宜发展生态农业,打造“生态特色水
果示范区”.该地区某水果树的单株年产量 (单位:千克)与单株施肥量x(单位:千克)之间的关系
为 ,且单株投入的年平均成本为 元.若这种水果的市场售价为10元/千克,且
水果销路畅通.记该水果树的单株年利润为 (单位:元).
(1)求函数 的解析式;
(2)求单株施肥量为多少千克时,该水果树的单株年利润最大?最大利润是多少?
例题2.(23-24高一下·浙江·阶段练习)空调是人们生活水平提高的一个标志,炎热夏天,空调使温度调
节到适合人们工作、学习、生活的舒适环境内,心情好,休息好,工作效率也高,这是社会进步的一个里
程碑.为适应市场需求,2024年某企业扩大了某型号的变频空调的生产,全年需投入固定成本200万元,
每生产x千台空调,需另投入成本 万元,当年产量不足30千台时, ,当年产量不小于
30千台时, .已知每台空调售价3000元,且生产的空调能全部销售完.
(1)写出年利润 (万元)关于年产量x(千台)的函数解析式.
(2)年产量为多少千台时,该厂该型号的变频空调所获利润最大?并求出最大利润.
精练
1.(23-24高一上·内蒙古呼和浩特·期中)某乡镇为了打造“网红”城镇发展经济,因地制宜的将该镇打造
成“生态水果特色小镇”.经调研发现:某珍惜水果树的单株产量W(单位:千克)与施用肥料x(单位:千
克)满足如下关系: ,肥料成本投入为10x元,其它成本投入(如培育管理、
施肥等人工费)20x元.已知这种水果的市场售价大约15元/千克,且销售畅通供不应求,记该水果单株利
润为 (单位:元)
学科网(北京)股份有限公司 学科网(北京)股份有限公司(1)写单株利润 (元)关于施用肥料x(千克)的关系式;
(2)当施用肥料为多少千克时,该水果单株利润最大?最大利润是多少?
2.(23-24高一上·浙江杭州·期中)第19届亚运会2023年9月在杭州市举办,本届亚运会以“绿色、智能、
节俭、文明”为办会理念,展示杭州生态之美、文化之韵,充分发挥国际重大赛事对城市发展的牵引作用,
从而促进经济快速发展.等备期间,计划向某河道投放水质净化剂,已知每投放a个单位( 且
)的试剂,它在水中释放的浓度y(克/升)随着时间x(天)变化的函数关系式近似为 ,
其中 ,若多次投放,则某一时刻水中的试剂浓度为每次投放的试剂在相应时刻所
释放的浓度之和,根据试验,当水中净化剂的浓度不低于4(克/升)时,它才能净化有效.
(1)若只投放一次4个单位的净化剂,则有效时间最多能持续几天?
(2)若先投放2个单位的净化剂,6天后再投放m个单位的净化剂,要使接下来的5天中,净化剂能够持续
有效,试求m的最小值.
对点特训五:对钩函数及其应用
典型例题
例题1.(23-24高一上·山东泰安·期中)2020年我国全面建成了小康社会,打赢了脱贫攻坚战. 某村全面
脱贫后,通过调整产业结构,以秀美乡村建设为契机,大力发展乡村旅游. 2021年上半年接待游客逾5万
人次,使该村成为当地旅游打卡网红景点. 该村原有 户从事种植业,据了解,平均每户的年收入为 万
元. 调整产业结构后,动员部分农户改行从事乡村旅游业. 据统计,若动员 户从事乡村旅游,
则剩下的继续从事种植业的平均每户的年收入有望提高 ,而从事乡村旅游的平均每户的年收入为
万元. 在动员 户从事乡村旅游后,还要确保剩下的 户从事种植业的所有农户年总
收入不低于原先 户从事种植的所有农户年总收入.
学科网(北京)股份有限公司 学科网(北京)股份有限公司(1)求 的取值范围;
(2)要使从事乡村旅游的这 户的年总收入始终不高于 户从事种植业的所有农户年总收入,求 的最
大值.
(参考数据: , , )
例题2.(23-24高二上·河南洛阳·期末)如图,某工厂欲将一块边长为40m的等边三角形ABC区域用一
条公共通道DE分成面积相等的两个办公区域,点D,E分别在AB,AC上,设 .(公共通道DE所
占面积忽略不计)
(1)令 ,求y关于x的函数关系式并写出定义域;
(2)若公共通道DE每米造价2000元,请你做一下预算,求出该通道造价最大值和最小值及对应的x值.
精练
1.(23-24高一下·四川攀枝花·期末)为了加强“平安校园”建设,保障师生安全,某校决定在学校门口利
用一侧原有墙体,建造一间墙高为3米,底面为24平方米,且背面靠墙的长方体形状的校园警务室.由于
此警务室的后背靠墙,无需建造费用,甲工程队给出的报价为:屋子前面新建墙体的报价为每平方米400
元,左右两面新建墙体报价为每平方米300元,屋顶和地面以及其他报价共计14400元.设屋子的左右两面
墙的长度均为 米 .
(1)当左右两面墙的长度为多少时,甲工程队报价最低?并求出最低报价;
(2)现有乙工程队也要参与此警务室的建造竞标,其给出的整体报价为 元 ,若无论左右
两面墙的长度为多少米,乙工程队都能竞标成功,试求 的取值范围.
学科网(北京)股份有限公司 学科网(北京)股份有限公司2.(23-24高一上·北京通州·期中)从2008年开始的十年间,中国高速铁路迅猛发展,已经建成“四纵四
横”网络,“八纵八横”格局正在构建.到2018年,中国高速铁路新里程已超过两万五千千米,铸就了一张新
的“国家名片”.京津城际高铁丛北京南站到天津站全长约为120千米.假设高铁每小时的运输成本(单位:万
元)由可变部分和固定部分组成;可变部分与平均速度 (千米/时)( )的平方成正比,比
例系数为0.0005;固定部分为 万元( ).设高速列车在该线路上单程运行一次的总费用为 .
(1)把高速列车在该线路上单程运行一次的总费用 表示成速度 (千米/时)的函数,并指出这个函数
的定义域;
(2)当高速列车在该线路上运行的平均速度是多少时,单程运行一次总费用最小?
一、单选题
1.(23-24高一·全国·课后作业)某机器总成本y(万元)与产量x(台)之间的函数关系式是y=x2-
75x,若每台机器售价为25万元,则该厂获利润最大时应生产的机器台数为( )
A.30 B.40
C.50 D.60
2.(23-24高一上·贵州遵义·阶段练习)面积为 的长方形的某边长度为 ,则该长方形的周长 与 的函
数关系为( )
A. B.
C. D.
3.(23-24高一·全国·课后作业)在自然界中,某种植物生长发育的数量y与时间x的关系如下表所示:
x 1 2 3 …
y 1 3 5 …
下面的函数关系式中,能表达这种关系的是( )
A. B.
C. D.
学科网(北京)股份有限公司 学科网(北京)股份有限公司4.(23-24高一上·宁夏银川·期中)某公司在甲、乙两地同时销售一种品牌车,销售 辆该品牌车的利润
(单位:万元)分别为 和 .若该公司在两地共销售15辆,则能获得的最大利润为
( )
A.90万元 B.60万元 C.120万元 D.120.25万元
5.(23-24高一上·江西·阶段练习)你见过古人眼中的烟花吗?那是朱淑真元宵夜的“火树银花触目红”,
是隋炀帝眼中的“灯树千光照,花焰七枝开”.烟花,虽然是没有根的花,是虚幻的花,却在达到最高点时爆
裂,用其灿烂的一秒换来人们真心的喝彩.已知某种烟花距地面的高度 (单位:米)与时间 (单位:
秒)之间的关系式为 ,则烟花在冲击后爆裂的时刻是( )
A.第4秒 B.第5秒 C.第3.5秒 D.第3秒
6.(23-24高一上·河南新乡·期末)某灯具商店销售一种节能灯,每件进价10元,每月销售量y(单位:
件)与销售价格x(单位:元)之间满足如下关系式: ( 且 ).则灯具商店
每月的最大利润为( )
A.3000元 B.4000元 C.3800元 D.4200元
7.(23-24高一上·浙江·阶段练习)如图,在 中, 于D, ,矩形的顶
点E与A点重合, ,将矩形 沿AB平移,当点E与点B重合时,停止平移,设点E平
移的距离为x,矩形 与 重合部分的面积为y,则y关于x 的函数图象大致为( )
A. B.
C. D.
8.(23-24高一上·湖南邵阳·期末)如图,点P在边长为1的正方形边上运动,M是CD的中点,当点P
沿 运动时,点P经过的路程x与 的面积y的函数 的图象的形状大致是
( )
学科网(北京)股份有限公司 学科网(北京)股份有限公司A. B.
C. D.
二、多选题
9.(23-24高一上·山西·期末)几名大学生创业时经过调研选择了一种技术产品,生产此产品获得的月利
润 (单位:万元)与每月投入的研发经费 (单位:万元)有关.已知每月投入的研发经费不高于16
万元,且 ,利润率 .现在已投入研发经费9万元,则下列判断正确的是
( )
A.此时获得最大利润率 B.再投入6万元研发经费才能获得最大利润
C.再投入1万元研发经费可获得最大利润率 D.再投入1万元研发经费才能获得最大利润
三、填空题
10.(2024·重庆·模拟预测)我国的酒驾标准是指车辆驾驶员血液中的酒精含量大于或者等于 ,
已知一驾驶员某次饮酒后体内每 血液中的酒精含量 (单位: )与时间 (单位: )的关系是:
当 时, ;当 时, ,那么该驾驶员在饮酒后至少要经过
才可驾车.
四、解答题
11.(23-24高一上·上海闵行·期中)某园林建设公司计划购买一批机器投入施工.据分析,这批机器可获
得的利润 (单位:万元)与运转时间 (单位:年)的函数解析式为 ( ,且
).
(1)当这批机器运转第几年时,可获得最大利润?最大利润为多少?
(2)当运转多少年时,这批机器的年平均利润最大?
学科网(北京)股份有限公司 学科网(北京)股份有限公司12.(2023·海南省直辖县级单位·模拟预测)某公司生产一类电子芯片,且该芯片的年产量不超过35万件,
每万件电子芯片的计划售价为16万元.已知生产此类电子芯片的成本分为固定成本与流动成本两个部分,
其中固定成本为30万元/年,每生产 万件电子芯片需要投入的流动成本为 (单位:万元),当年产
量不超过14万件时, ;当年产量超过14万件时, .假设该公司每年
生产的芯片都能够被销售完.
(1)写出年利润 (万元)关于年产量 (万件)的函数解析式;(注:年利润=年销售收入-固定成本
-流动成本)
(2)如果你作为公司的决策人,为使公司获得的年利润最大,每年应生产多少万件该芯片?
学科网(北京)股份有限公司 学科网(北京)股份有限公司