文档内容
曲线运动知识点总结
一、曲线运动
1.定义:物体运动轨迹是曲线的运动。
2.条件:运动物体所受合力的方向跟它的速度方向不在同一直线上。
3.特点:①方向:某点瞬时速度方向就是通过这一点的曲线的切线方向。
②运动类型:变速运动(速度方向不断变化)。
③F ≠ 0,一定有加速度 a。
合
④F 方向一定指向曲线凹侧。
合
二、运动的合成与分解
1.合运动与分运动的关系: 等时性 、 独立性 、等效性、同体性。
2.互成角度的两个分运动的合运动的判断:(判断合初速度与合加速度的方向是否共线)
①两个匀速直线运动的合运动仍然是匀速直线运动。
②速度方向不在同一直线上的两个分运动,一个是匀速直线运动,一个是匀变速直线运动,
其合运动是匀变速曲线运动,a 为分运动的加速度。
合
③两初速度为0的匀加速直线运动的合运动仍然是匀加速直线运动。
④两个初速度不为0的匀加速直线运动的合运动可能是直线运动也可能是曲线运动。当两
个分运动的合初速度方向与这两个分运动的和合加速度在同一直线上时,合运动是匀变速
直线运动,否则即为匀变速曲线运动。
三、运动的合成与分解两大题型
1.小船过河问题
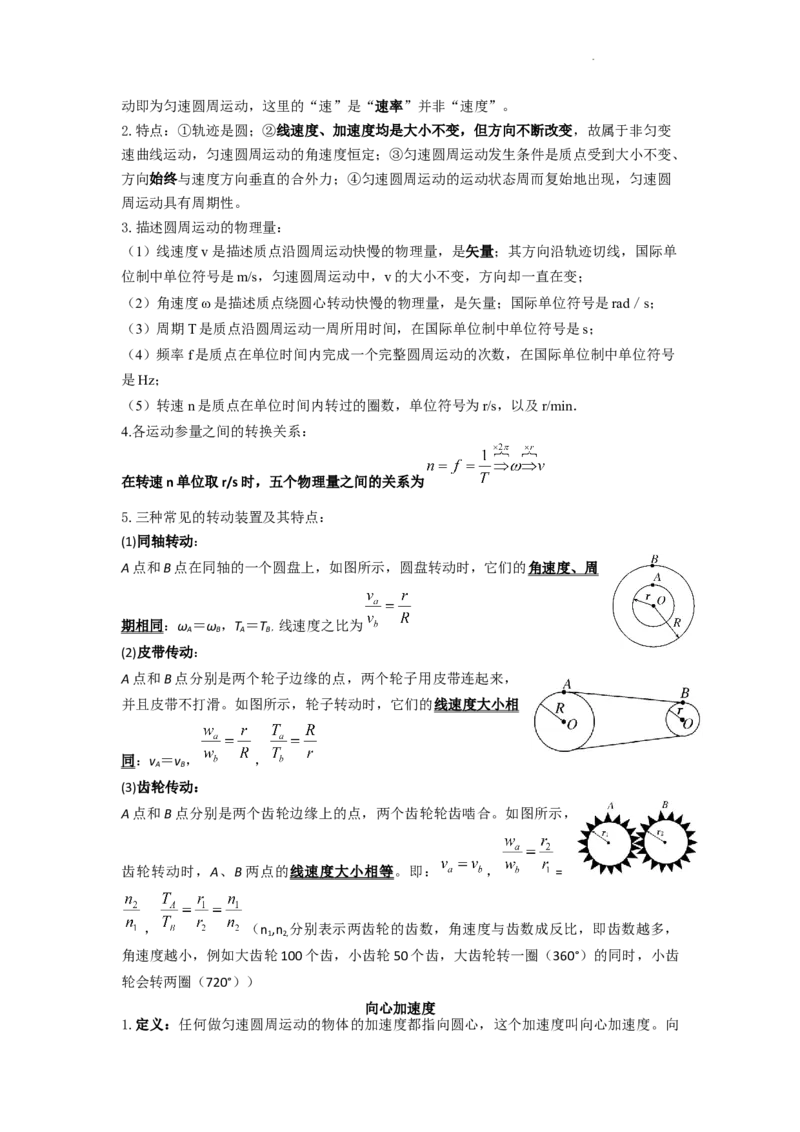
模型一:过河时间t最短:
船头 垂直于河岸 渡河时间最短 ,渡河时间t为河宽d/船在静水中的速度v
船
小船的合速度为
小船的位移为合速度乘渡河时间,即
模型二:渡河位移x最短(分为能否到达正对岸两种情况)
①无论船速大还是水速大,合速度都为两者较大者与较小者的平
方差的平方根,即
②根据船速与水速谁大判断合位移,若船速较大,则合位移为河
宽d,若水速较大,则合位移为s == d. .(记忆技巧,由
短
于此时船不能到达正对岸,所以最短位移 s 肯定比河宽d大,那
短
么这俩速度比就是大速度比小速度了,即水速比船速)
α 为船头与河岸上游的夹角,当船速比较大时, ,当水速比较大时,
(其实就是小的比大的,结合数学知识余弦函数小于1来理解记忆)
学科网(北京)股份有限公司③渡河时间直接用合位移比上合速度就可以了
2.速度“关联”问题
以物体与绳子或杆的连接点为研究对象,把物体的实际速度分解为垂直于绳(杆)和平行于
绳(杆)两个分量,根据沿绳(杆)方向的分速度大小相等求解.
四、平抛运动
抛体运动
1.定义:以一定的速度将物体抛出,在空气阻力可以忽略的情况下,物体只受重力的作用,
它的运动即为抛体运动。
2.条件:①物体具有初速度;②运动过程中只受重力。
平抛运动
1.定义:如果物体运动的初速度是沿水平方向的,这个运动就叫做平抛运动。
2.条件:①物体具有 水平 方向 的初速度;②运动过程中只受重力。
3.处理方法:平抛运动可以看作两个分运动的合运动:一个是水平方向的匀速直线运动,
一个是竖直方向的自由落体运动。
4.规律:
(1)位 移 :
gt
tanα=
v =v v =gt v= √v2 +(gt) 2 v
(2)速度: x 0, y , 0 , 0
(3)推论:①从抛出点开始,任意时刻速度偏向角 的正切值等于位移偏向角 的正切
1
gt2
gt
2 gt
tanα= tanθ= = .
v v t 2v
值的两倍。 证明如下: 0 , 0 0 。
②从抛出点开始,任意时刻速度的反向延长线对应的水平位移的交点为此水平位移的中点
2y
tanθ= .
x
即 如果物体落在斜面上,则位移偏向角与斜面倾角相等。
5.应用结论——影响做平抛运动的物体的飞行时间、射程及落地速度的因素
a、飞行时间: , t 仅仅与物体下落高度 h 有关 ,与初速度v 无关。(重点记忆)
0
b、水平射程: 由v 和h共同决定。(会推导即可)
0
c、落地速度: ,v由v 和v 共同决定。
0 y
由于平抛运动是应用运动的合成与分解方法来解决的,所以独立性和等时性这两个性质十
分重要,时间是解决平抛运动问题的关键,而时间仅仅由下落高度决定,无论怎样的题型
都要以时间为纽带,进而求解其它物理量
五、圆周运动
匀速圆周运动
1.定义:物体的运动轨迹是圆的运动叫做圆周运动,物体运动的线速度大小不变的圆周运
学科网(北京)股份有限公司动即为匀速圆周运动,这里的“速”是“速率”并非“速度”。
2.特点:①轨迹是圆;②线速度、加速度均是大小不变,但方向不断改变,故属于非匀变
速曲线运动,匀速圆周运动的角速度恒定;③匀速圆周运动发生条件是质点受到大小不变、
方向始终与速度方向垂直的合外力;④匀速圆周运动的运动状态周而复始地出现,匀速圆
周运动具有周期性。
3.描述圆周运动的物理量:
(1)线速度v是描述质点沿圆周运动快慢的物理量,是矢量;其方向沿轨迹切线,国际单
位制中单位符号是m/s,匀速圆周运动中,v的大小不变,方向却一直在变;
(2)角速度ω是描述质点绕圆心转动快慢的物理量,是矢量;国际单位符号是rad/s;
(3)周期T是质点沿圆周运动一周所用时间,在国际单位制中单位符号是s;
(4)频率f是质点在单位时间内完成一个完整圆周运动的次数,在国际单位制中单位符号
是Hz;
(5)转速n是质点在单位时间内转过的圈数,单位符号为r/s,以及r/min.
4.各运动参量之间的转换关系:
在转速n单位取r/s时,五个物理量之间的关系为
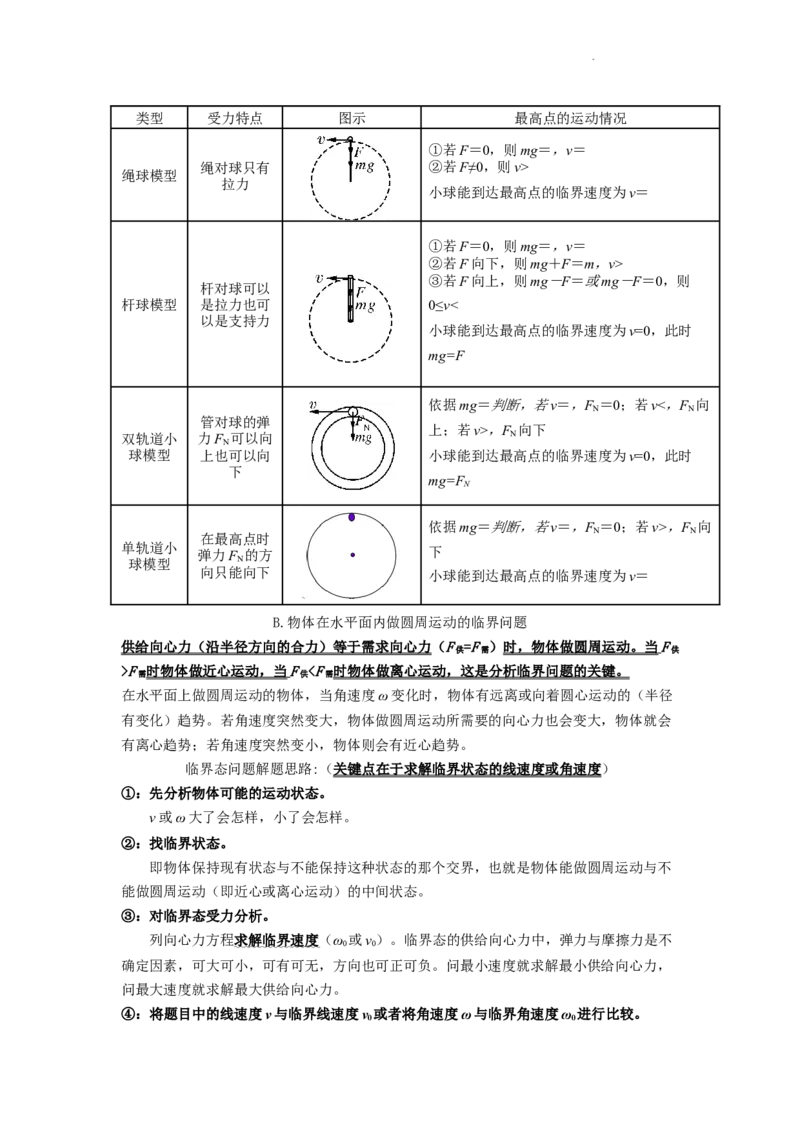
5.三种常见的转动装置及其特点:
(1)同轴转动:
A点和B点在同轴的一个圆盘上,如图所示,圆盘转动时,它们的角速度、周
期相同:ω =ω ,T=T 线速度之比为
A B A B,
(2)皮带传动:
A点和B点分别是两个轮子边缘的点,两个轮子用皮带连起来,
并且皮带不打滑。如图所示,轮子转动时,它们的线速度大小相
同:v =v , ,
A B
(3)齿轮传动:
A点和B点分别是两个齿轮边缘上的点,两个齿轮轮齿啮合。如图所示,
齿轮转动时,A、B两点的 线速度 大小相等 。即: , =
, (n ,n 分别表示两齿轮的齿数,角速度与齿数成反比,即齿数越多,
1 2,
角速度越小,例如大齿轮100个齿,小齿轮50个齿,大齿轮转一圈(360°)的同时,小齿
轮会转两圈(720°))
向心加速度
1.定义:任何做匀速圆周运动的物体的加速度都指向圆心,这个加速度叫向心加速度。向
学科网(北京)股份有限公司心加速度的方向永远指向圆心。
2.向心加速度与实际加速度的关系:只有物体做匀速圆周运动时,物体实际的加速度才等
于向心加速度;若物体做变速圆周运动,向心加速度只是实际的加速度的径向分量,两者
不等(另一个分量是切向加速度)。
3.方向:在匀速圆周运动中,始终指向圆心,始终与线速度的方向垂直。向心加速度只改
变线速度的方向而非大小。
4.意义:描述圆周运动速度方向改变快慢的物理量。
4.公式:
向心力
1.定义:做圆周运动的物体所受到的沿着半径指向圆心的合力,叫做向心力。
2.方向:总是指向圆心。
3.公式: (适用于任何圆周运
动)
4.判断向心力来源的技巧:只要物体做的是圆周运动,那不管物体是做匀速圆周运动还是
变速圆周运动,其向心力永远都是物体所受沿半径方向的力的合力,并且其方向指向圆心。
(一定要记牢)
5.匀速圆周运动与变速圆周运动的本质区别在于:合外力是否全部用来提供向心力
匀速圆周运动中向心力就是物体所受的实际合外力(即合外力全部用来提供向心力,
此时物体所受合外力沿径向指向圆心,始终与速度方向垂直,切向方向无分力,不改变速
度的大小,只改变速度的方向,因此做匀速圆周运动),合外力=向心力。
变速圆周运动中,向心力只不过是物体所受实际合外力在半径方向的分力(即合外力
不全部用来提供向心力,合外力并不指向圆心,若把合外力正交分解可分为径向分力与切
向分力,径向分力即为向心力,只改变速度的方向,切向分力与速度方向共线,只改变速
度的大小)合外力≠向心力。
6.几个注意点:①在受力分析时,只分析性质力,而不分析效果力,因此在受力分析时,
不要加上向心力。②描述做匀速圆周运动的物体时,不能说该物体受向心力,而是说该物
体受到什么力,这几个力的合力充当或提供向心力。
离心运动:
(1)当物体实际受到的沿半径方向的合力满足 F =F =mω2r时,物体做圆周运动;当F
供 需
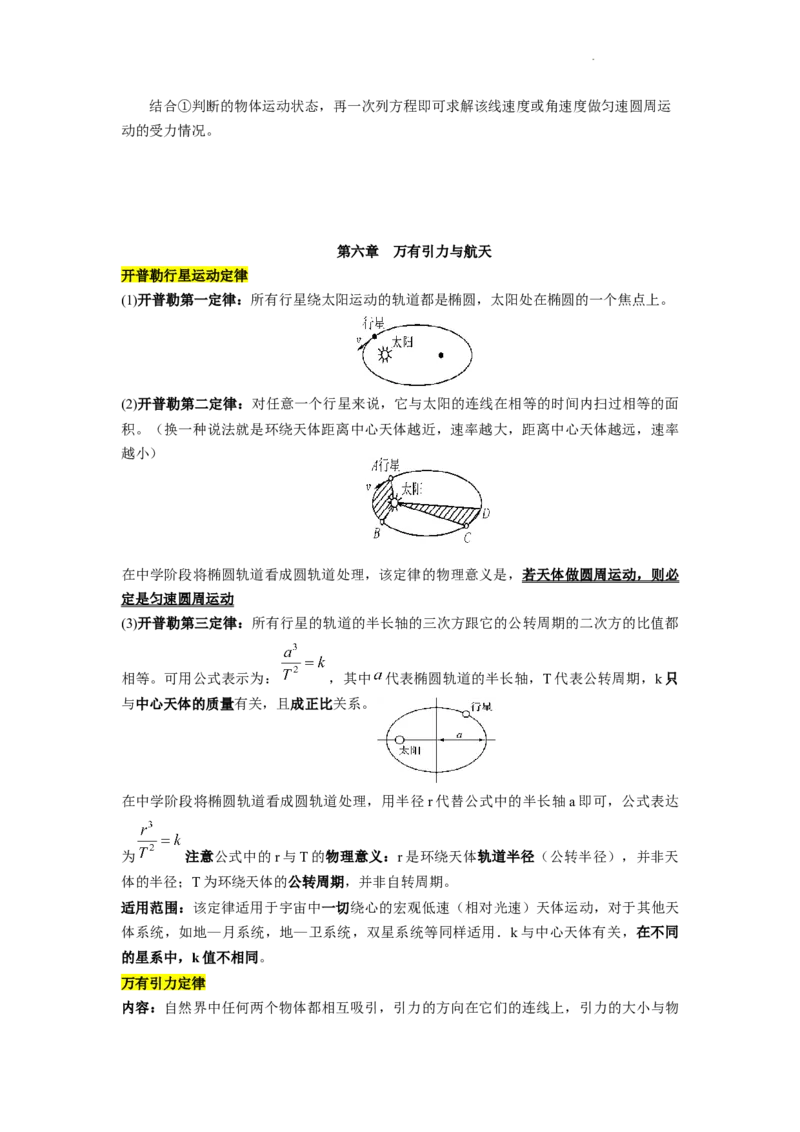
绳球模型
拉力
小球能到达最高点的临界速度为v=
①若F=0,则mg=,v=
②若F向下,则mg+F=m,v>
③若F向上,则mg-F=或mg-F=0,则
杆对球可以
杆球模型 是拉力也可 0≤v<
以是支持力
小球能到达最高点的临界速度为v=0,此时
mg=F
依据mg=判断,若v=,F =0;若v<,F 向
N N
管对球的弹
上;若v>,F 向下
双轨道小 力F 可以向 N
N
球模型 上也可以向 小球能到达最高点的临界速度为v=0,此时
下
mg=F
N
依据mg=判断,若v=,F =0;若v>,F 向
N N
在最高点时
单轨道小 弹力F 的方 下
球模型 N
向只能向下 小球能到达最高点的临界速度为v=
B.物体在水平面内做圆周运动的临界问题
供给向心力(沿半径方向的合力)等于需求向心力(F =F )时,物体做圆周运动。当 F
供 需 供
>F 时物体做近心运动,当 F