文档内容
期中检测卷 01
姓名:__________________ 班级:______________ 得分:_________________
注意事项:
本试卷满分150分,考试时间120分钟,试题共22题.答卷前,考生务必用0.5毫米黑色签字笔将自
己的姓名、班级等信息填写在试卷规定的位置.
一、选择题(本大题共8小题,每小题5分,共40分)在每小题所给出的四个选项中,只有一项是符合题
目要求的.
1.已知复平面内,(2﹣i)z对应的点位于虚轴的正半轴上,则复数z对应的点位于( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
【答案】B
【分析】直接利用复数的运算和几何意义的应用求出该点所表示的位置.
【解答】解:设z=a+bi(a,b R),
所以(2﹣i)(a+bi)=2a+b+(2b﹣a)i,
∈
由于对应的点在虚轴的正半轴上,
所以 ,
即 ,
所以a<0,b>0.
故该点在第二象限.
故选:B.
【知识点】复数的代数表示法及其几何意义
2.平行四边形ABCD中,点E是DC的中点,点F是BC的一个三等分点(靠近B),则 =( )
A. B. C. D.
【答案】D
【分析】利用平行四边形的性质以及向量相等的概念,再利用平面向量基本定理进行转化即可.
【解答】解:因为ABCD为平行四边形,
所以 ,故 .
故选:D.
【知识点】平面向量的基本定理
3.已知向量 =(6t+3,9), =(4t+2,8),若( + )∥( ﹣ ),则t=( )
A.﹣1 B.﹣ C. D.1
【答案】B
【分析】根据平面向量的坐标表示和共线定理,列方程求出t的值.
【解答】解:向量 =(6t+3,9), =(4t+2,8),
所以 + =(6t+3,11),
﹣ =(4t+2,5).
又( + )∥( ﹣ ),
所以5(6t+3)﹣11(4t+2)=0,
解得t=﹣ .
故选:B.
【知识点】平面向量共线(平行)的坐标表示
4.已知矩形ABCD的一边AB的长为4,点M,N分别在边BC,DC上,当M,N分别是边BC,DC的中点
时,有( + )• =0.若 + =x +y ,x+y=3,则线段MN的最短长度为( )
A. B.2 C.2 D.2
【答案】D
【分析】先根据M,N满足的条件,将( + )• =0化成 的表达式,从而判断出矩形ABCD
为正方形;再将 + =x +y ,左边用 表示出来,结合x+y=3,即可得NC+MC=
4,最后借助于基本不等式求出MN的最小值.
【解答】解:当M,N分别是边BC,DC的中点时,
有 ( + ) • = = =,
所以AD=AB,则矩形ABCD为正方形,
设 , ,则 = .
则x=2﹣ ,y=2﹣ .又x+y=3,所以 + =1.
λ μ λ μ
故NC+MC=4,则MN= = (当且仅当MC=NC=2时
取等号).
故线段MN的最短长度为2 .
故选:D.
【知识点】平面向量数量积的性质及其运算
5.若z C且|z+3+4i|≤2,则|z﹣1﹣i|的最大和最小值分别为M,m,则M﹣m的值等于( )
A.∈3 B.4 C.5 D.9
【答案】B
【分析】由题意画出图形,再由复数模的几何意义,数形结合得答案.
【解答】解:由|z+3+4i|≤2,得z在复平面内对应的点在以Q(﹣3,﹣4)为圆心,以2为半径的圆及其内
部.
如图:
|z﹣1﹣i|的几何意义为区域内的动点与定点P得距离,
则M=|PQ|+2,m=|PQ|﹣2,
则M﹣m=4.
故选:B.
【知识点】复数的运算
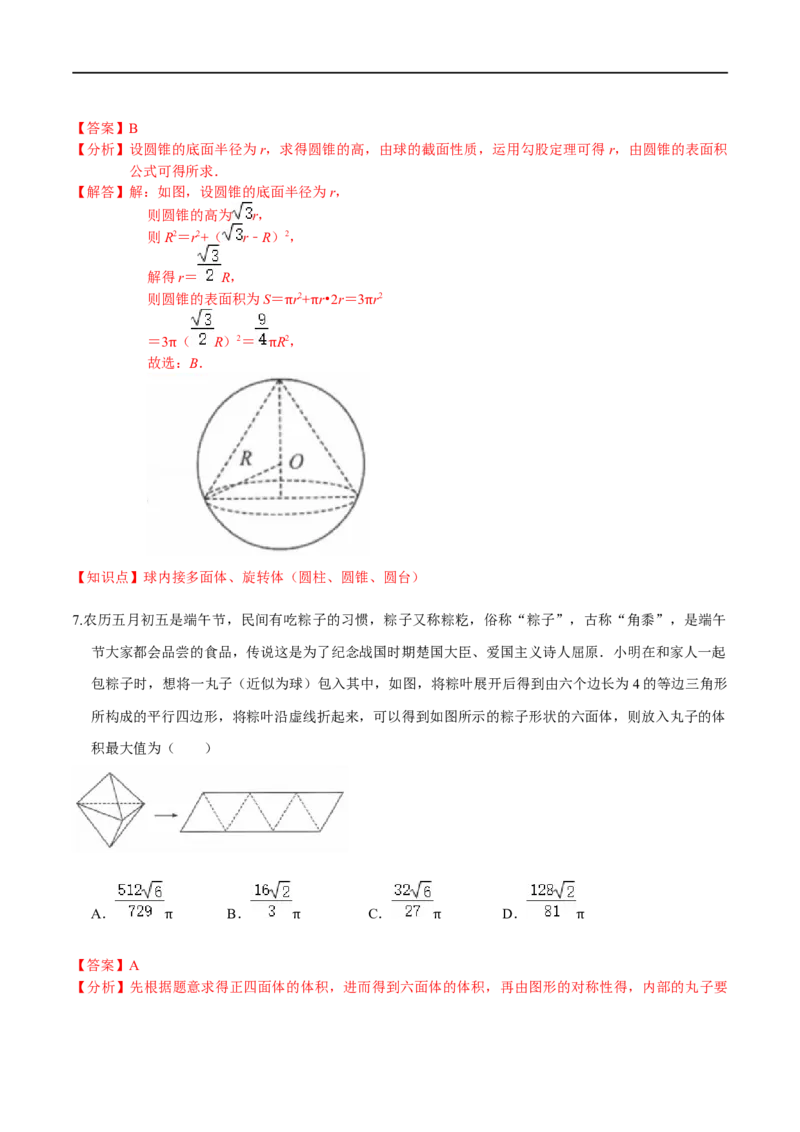
6.已知球的半径为R,一等边圆锥(圆锥母线长与圆锥底面直径相等)位于球内,圆锥顶点在球上,底面
与球相接,则该圆锥的表面积为( )
A. R2 B. R2 C. R2 D. R2【答案】B
【分析】设圆锥的底面半径为r,求得圆锥的高,由球的截面性质,运用勾股定理可得r,由圆锥的表面积
公式可得所求.
【解答】解:如图,设圆锥的底面半径为r,
则圆锥的高为 r,
则R2=r2+( r﹣R)2,
解得r= R,
则圆锥的表面积为S= r2+ r•2r=3 r2
π π π
=3 ( R)2= R2,
故选:B.
π π
【知识点】球内接多面体、旋转体(圆柱、圆锥、圆台)
7.农历五月初五是端午节,民间有吃粽子的习惯,粽子又称粽籺,俗称“粽子”,古称“角黍”,是端午
节大家都会品尝的食品,传说这是为了纪念战国时期楚国大臣、爱国主义诗人屈原.小明在和家人一起
包粽子时,想将一丸子(近似为球)包入其中,如图,将粽叶展开后得到由六个边长为4的等边三角形
所构成的平行四边形,将粽叶沿虚线折起来,可以得到如图所示的粽子形状的六面体,则放入丸子的体
积最大值为( )
A. B. C. D.
π π π π
【答案】A
【分析】先根据题意求得正四面体的体积,进而得到六面体的体积,再由图形的对称性得,内部的丸子要是体积最大,就是丸子要和六个面相切,设丸子的半径为R,则 ,由此
求得R,进而得到答案.
【解答】解:由题意可得每个三角形面积为 ,
由对称性可知该六面体是由两个正四面体合成的,可得该四面体的高为 ,
故四面体的体积为 ,
∵该六面体的体积是正四面体的2倍,
∴六面体的体积是 ,
由图形的对称性得,内部的丸子要是体积最大,就是丸子要和六个面相切,连接球心和五个顶
点,把六面体分成了六个三棱锥,
设丸子的半径为R,则 ,解得 ,
∴丸子的体积的最大值为 .
故选:A.
【知识点】棱柱、棱锥、棱台的体积
8.已知半球O与圆台OO'有公共的底面,圆台上底面圆周在半球面上,半球的半径为1,则圆台侧面积取最
大值时,圆台母线与底面所成角的余弦值为( )
A. B. C. D.
【答案】D
【分析】根据题意画出图形,结合图形利用圆台的母线长表示出半球的半径r,计算圆台的侧面积,利用
导数求得侧面积取得最大值时对应的母线长和半球的半径,从而求得圆台母线与底面所成角的余
弦值.
【解答】解:如图1所示,
设BC=x,CO′=r,作CF⊥AB于点F,延长OO′交球面于点E,
则BF=1﹣r,OO′=CF= = .
由圆的相交弦定理和图2知,CO′•O′E•O′H=(1+OO′)•(1﹣OO′),即r2=(1+ )•(1﹣ ),解得r=1﹣ ,
所以圆台的侧面积为S = •(1+1﹣ )•x(0<x< );
侧
π
求导数得S ′= (2﹣ x2),令S =0,得出当x= 时S 取得最大值,
侧 侧 侧
π
所以当x=BC= 时,r=1﹣ = ,
则BF=1﹣r= ;
在轴截面中,∠OBC为圆台母线与底面所成的角,
在Rt△CFB中,cos∠OBC= = .
故选:D.
【知识点】旋转体(圆柱、圆锥、圆台)
二、多选题(本大题共4小题,每小题5分,选对得分,选错、少选不得分)
9.下列有关向量命题,不正确的是( )
A.若| |=| |,则 = B.已知 ≠ ,且 • = • ,则 =
C.若 = , = ,则 = D.若 = ,则| |=| |且 ∥
【答案】AB
【分析】根据向量的概念与向量的模的概念逐一分析各个选项即可得解.
【解答】解:向量由两个要素方向和长度描述,A错误;
若 ∥ ,且与 垂直,结果成立,当 不一定等于 ,B错误;
若 = , = ,由向量的定义可得 = ,C正确;
相等向量模相等,方向相同,D选项正确.
故选:AB.
【知识点】向量的概念与向量的模
10.若复数z满足 ,则( )
A.z=﹣1+i B.z的实部为1 C. =1+i D.z2=2i【答案】BC
【分析】把已知等式变形,再由复数代数形式的乘除运算化简,然后逐一核对四个选项得答案.
【解答】解:由 = ,
得z= ,
∴z的实部为1; =1+i;z2=(1﹣i)2=﹣2i.
故选:BC.
【知识点】复数的运算
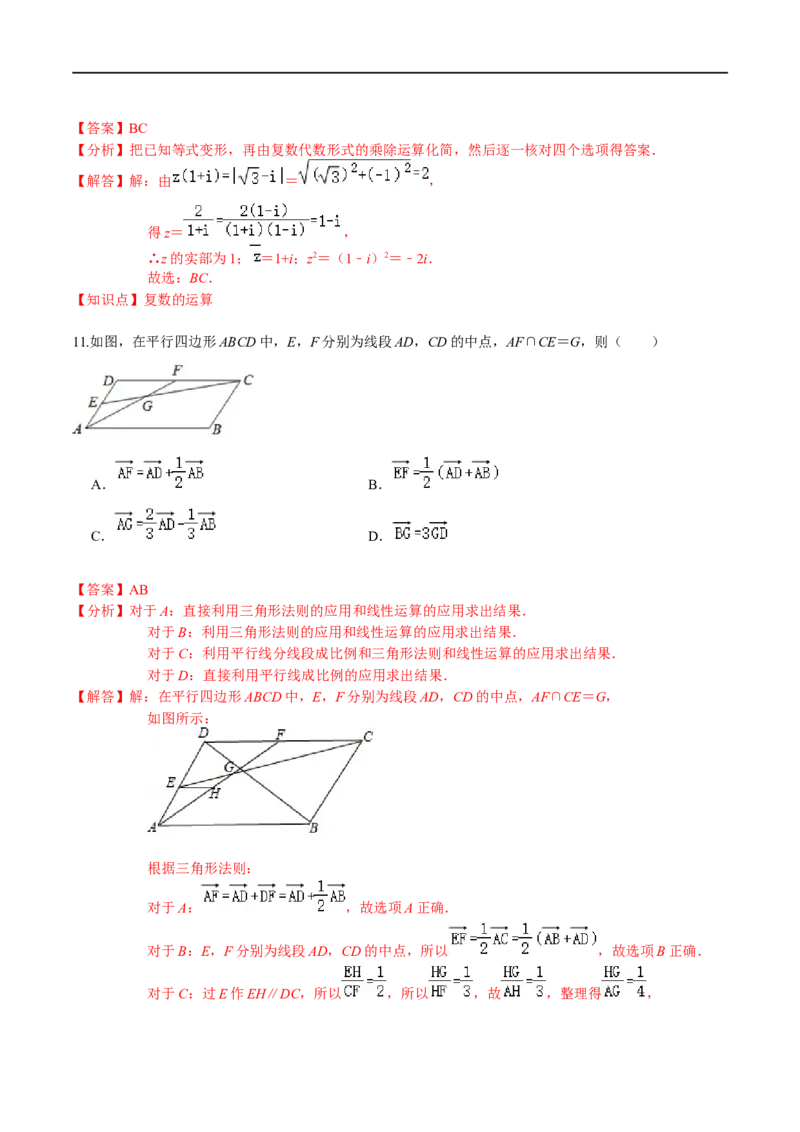
11.如图,在平行四边形ABCD中,E,F分别为线段AD,CD的中点,AF∩CE=G,则( )
A. B.
C. D.
【答案】AB
【分析】对于A:直接利用三角形法则的应用和线性运算的应用求出结果.
对于B:利用三角形法则的应用和线性运算的应用求出结果.
对于C:利用平行线分线段成比例和三角形法则和线性运算的应用求出结果.
对于D:直接利用平行线成比例的应用求出结果.
【解答】解:在平行四边形ABCD中,E,F分别为线段AD,CD的中点,AF∩CE=G,
如图所示:
根据三角形法则:
对于A: ,故选项A正确.
对于B:E,F分别为线段AD,CD的中点,所以 ,故选项B正确.
对于C:过E作EH∥DC,所以 ,所以 ,故 ,整理得 ,所以 ,即 = ,故选项C错误.
对于D:根据平行线分线段成比例定理,点B、G、D共线, 故选项D错误.
故选:AB.
【知识点】平面向量的基本定理
12.已知正方体ABCD﹣ABC D ,棱长为2,E为线段BC上的动点,O为AC的中点,P为棱CC 上的动
1 1 1 1 1 1
点,Q为棱AA 的中点,则以下选项中正确的有( )
1
A.AE⊥BC
1
B.直线BD⊥平面ABC
1 1 1
C.异面直线AD 与OC 所成角为
1 1
D.若直线m为平面BDP与平面BDP的交线,则m∥平面BDQ
1 1 1 1
【答案】BD
【分析】根据面面平行和垂直的性质、判定,结合图形,从而可判断选项的正误.
【解答】解:在正方体ABCD﹣ABC D 中,BC⊥BC ,BC⊥AB,BC ∩AB=B,
1 1 1 1 1 1 1 1
∴BC⊥平面ABCD,
1 1 1
∵只有当E运动到线段BC的中点时,AE⊥BC才成立,故A错误.
1 1
连接BD,∵在正方体ABCD﹣ABC D 中,DD ⊥平面ABC D,
1 1 1 1 1 1 1 1 1 1 1
∴DD ⊥AC ,∵BD⊥AC ,BD∩DD =D,
1 1 1 1 1 1 1 1 1
∴AC ⊥平面BDD B,∴AC ⊥BD,
1 1 1 1 1 1 1
同理可得BC ⊥BD,又AC ∩BC =C ,
1 1 1 1 1 1
∴直线BD⊥平面ABC ,故选项B正确.
1 1 1
连接BD,BC ,则AD∥BC ,
1 1 1
∴∠OC B(或其补角)即为异面直线AD 与OC 所成的角.
1 1 1
因为正方体的棱长为2,则BC =2 ,OB= ,在Rt△C OB中,OC = ,
1 1 1
∴cos∠OC B= = ,∴∠OC B= ,故选项C错误.
1 1
由题意知,在正方体ABCD﹣ABC D 中,P为棱CC 上的动点,Q为棱AA 的中点,
1 1 1 1 1 1
直线m为平面BDP与平面BDP的交线,且BD∥BD,
1 1 1 1
∴m∥BD.∵m 平面BDQ,
1 1 1 1
∴m∥平面BDQ,故选项D正确.
1 1
⊄
故选:BD.【知识点】空间中直线与平面之间的位置关系、异面直线及其所成的角、直线与平面垂直、命题的真假判
断与应用
三、填空题(本大题共4小题,每小题5分,共20 分.不需写出解答过程,请把答案直接填写在横线
上)
13.已知向量 =(m,1), =(m﹣6,m﹣4),若 ∥ ,则m的值为 .
【答案】2或3
【分析】根据题意,由向量平行的坐标表示方法可得(m﹣4)m﹣(m﹣6)=0,变形解可得m的值,即
可得答案.
【解答】解:根据题意,知向量 =(m,1), =(m﹣6,m﹣4),
若 ∥ ,则有(m﹣4)m﹣(m﹣6)=0,
变形可得:m2﹣5m+6=0,
解可得m=2或3,
故答案为:2或3.
【知识点】平面向量共线(平行)的坐标表示
14.将表面积为36 的圆锥沿母线将其侧面展开,得到一个圆心角为 的扇形,则该圆锥的轴截面的面积
S= . π
【分析】设圆锥的母线长为l,底面半径为r,根据题意列出方程组求出l和r的值,再计算圆锥的高轴截
面面积.
【解答】解:设圆锥的母线长为l,底面半径为r,由题意得 ,
解得l=9,r=3;
所以圆锥的高为h= = =6 ,
所以圆锥的轴截面面积为S= × =18 .
故答案为:18 .
【知识点】旋转体(圆柱、圆锥、圆台)、扇形面积公式
15.如图,已知有两个以O为圆心的同心圆,小圆的半径为1,大圆的半径为2,点A为小圆上的动点,点
P,Q是大圆上的两个动点,且 • =1,则| |的最大值是 .
【分析】由向量的和差运算求出数量积 • 的表达式,再由| |的值为1,可得 ﹣ ﹣
=0,再由( + ﹣ )2的展开可得| + ﹣ |=3,再由绝对值不等式的定理可得| |
的取值范围,求出其最大值.
【解答】解:由题意 =( ﹣ )•( ﹣ )= ﹣ ﹣ +1=1,
所以 ﹣ ﹣ =0,
由( + ﹣ )2= + 2+ 2+2( ﹣ ﹣ )=9,
所以| + ﹣ |=3,
又| + |﹣| |≤| + ﹣ |≤| + |+| |,
所以2≤| + |≤4,
又| + |2+| ﹣ |2=2(| |2+| |2)=16,所以0≤| ﹣ | ,
即0≤| | ,
| |的最大值是2 ,
故答案为:2 .
【知识点】平面向量数量积的性质及其运算
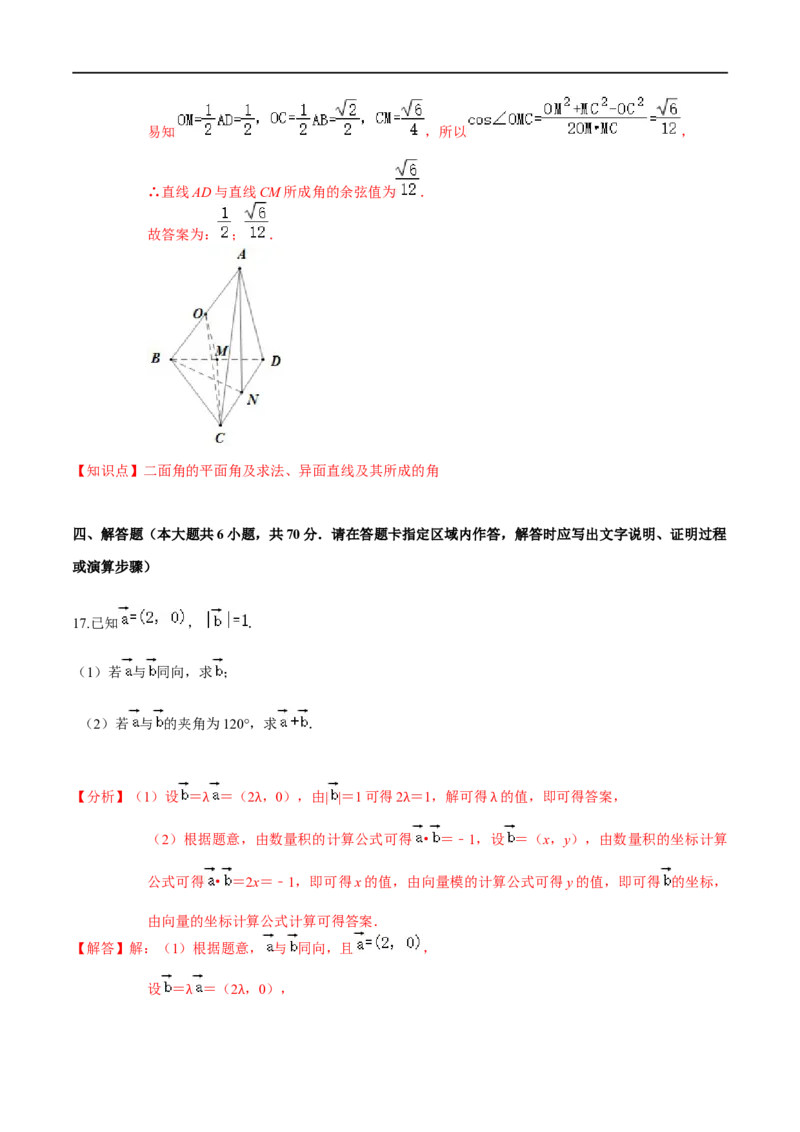
16.如图,在三棱锥A﹣BCD的平面展开图中,已知四边形BCED为菱形,BC=1,BF= ,若二面角A
﹣CD﹣B的余弦值为﹣ ,M为BD的中点,则CD= ,直线AD与直线CM所成角的余弦值为
.
【分析】将三棱锥A﹣BCD的直观图还原,取CD中点N,连接AN,BN,可知ANB为二面角A﹣CD﹣B
的平面角,设CD=a(0<a<2),根据题意由余弦定理建立关于a的方程,解出即可求得CD的
值,取AB的中点O,连接OM,OC,则∠OMC为直线AD与直线CM所成的角或其补角,求出
相关边的长度,利用余弦定理直接求解即可.
【解答】解:将三棱锥A﹣BCD的直观图还原,则BC=BD=AC=AD=1, ,
取CD中点N,连接AN,BN,则AN⊥CD,BN⊥CD,故∠ANB为二面角A﹣CD﹣B的平面角,
设CD=a(0<a<2),则 ,故 ,
又二面角A﹣CD﹣B的余弦值为 ,故 ,解得 ,即 ;
取AB的中点O,连接OM,OC,易知OM∥AD,
所以∠OMC为直线AD与直线CM所成的角或其补角,易知 ,所以 ,
∴直线AD与直线CM所成角的余弦值为 .
故答案为: ; .
【知识点】二面角的平面角及求法、异面直线及其所成的角
四、解答题(本大题共6小题,共70分.请在答题卡指定区域内作答,解答时应写出文字说明、证明过程
或演算步骤)
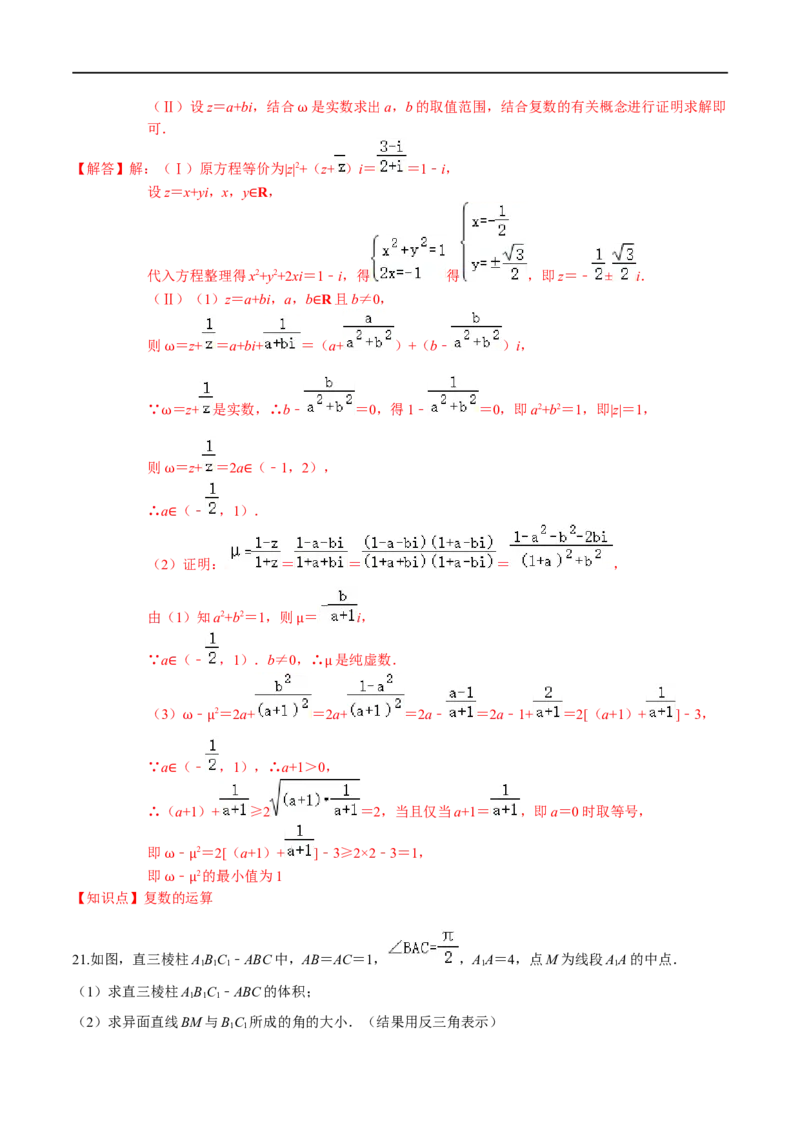
17.已知 , .
(1)若 与 同向,求 ;
(2)若 与 的夹角为120°,求 .
【分析】(1)设 = =(2 ,0),由| |=1可得2 =1,解可得 的值,即可得答案,
λ λ λ λ
(2)根据题意,由数量积的计算公式可得 • =﹣1,设 =(x,y),由数量积的坐标计算
公式可得 • =2x=﹣1,即可得x的值,由向量模的计算公式可得y的值,即可得 的坐标,
由向量的坐标计算公式计算可得答案.
【解答】解:(1)根据题意, 与 同向,且 ,
设 = =(2 ,0),
λ λ又由| |=1,则有2 =1,即 = ,
则 =(1,0);
λ λ
(2) ,则| |=2,
若 与 的夹角为120°,则 • =| || |cos120°=2×1×cos120°=﹣1,
设 =(x,y),则 • =2x=﹣1,则x=﹣ ,
又由| |=1,则x2+y2=1,解可得y=± ,
故 =( ,± ),
则 + =( ,± ).
【知识点】平面向量数量积的性质及其运算、数量积表示两个向量的夹角
18.已知a、b、c是△ABC中∠A、∠B、∠C的对边,a=4 ,b=6,cosA=﹣ .
(1)求c;
(2)求cos2B的值.
【分析】(1)由余弦定理即可求得c的值;
(2)先由同角三角函数的平方关系求得sinA的值,再由正弦定理求出sinB的值,最后根据
cos2B=1﹣2sin2B,得解.
【解答】解:(1)由余弦定理知,a2=b2+c2﹣2bccosA,即48=36+c2﹣2×6×c×(﹣ ),
整理得,c2+4c﹣12=0,
解得c=2或﹣6(舍负),
故c=2.
(2)∵cosA=﹣ ,且A (0, ),
∈ π
∴sinA= = ,
由正弦定理知, = ,即 = ,
∴sinB= ,
∴cos2B=1﹣2sin2B=﹣ .【知识点】余弦定理
19.已知:复数z 与z 在复平面上所对应的点关于y轴对称,且z(1﹣i)=z(1+i)(i为虚数单位),|z|
1 2 1 2 1
= .
(Ⅰ)求z 的值;
1
(Ⅱ)若z 的虚部大于零,且 (m,n R),求m,n的值.
1
∈
【分析】(Ⅰ)设z=x+yi(x,y R),则z=﹣x+yi,由题意列方程组求得x,y的值,则答案可求;
1 2
∈
(Ⅱ)求得z ,代入 ,利用复数代数形式的乘除运算化简化简,再由复数相等的
1
条件求解.
【解答】解:(Ⅰ)设z=x+yi(x,y R),则z=﹣x+yi,
1 2
∵z(1﹣i)=z(1+i),|z|= ,
1 2 ∈1
∴ ,解得 或 ,
即z=1﹣i或z=﹣1+i;
1 1
(Ⅱ)∵z 的虚部大于零,∴z=﹣1+i,则 ,
1 1
则有 ,
∴ ,解得 .
【知识点】复数的运算
20.(Ⅰ)在复数范围内解方程|z|2+(z+ )i= (i为虚数单位)
(Ⅱ)设z是虚数, =z+ 是实数,且﹣1< <2.
(1)求|z|的值及z的ω实部的取值范围; ω
(2)设 ,求证: 为纯虚数;
(3)在(2)的条件下求 μ﹣ 2的最小值.
ω μ
【分析】(Ⅰ)利用待定系数法,结合复数相等进行求解即可(Ⅱ)设z=a+bi,结合 是实数求出a,b的取值范围,结合复数的有关概念进行证明求解即
可.
ω
【解答】解:(Ⅰ)原方程等价为|z|2+(z+ )i= =1﹣i,
设z=x+yi,x,y R,
∈
代入方程整理得x2+y2+2xi=1﹣i,得 得 ,即z=﹣ ± i.
(Ⅱ)(1)z=a+bi,a,b R且b≠0,
∈
则 =z+ =a+bi+ =(a+ )+(b﹣ )i,
ω
∵ =z+ 是实数,∴b﹣ =0,得1﹣ =0,即a2+b2=1,即|z|=1,
ω
则 =z+ =2a (﹣1,2),
ω ∈
∴a (﹣ ,1).
∈
(2)证明: = = = ,
由(1)知a2+b2=1,则 = i,
μ
∵a (﹣ ,1).b≠0,∴ 是纯虚数.
∈ μ
(3) ﹣ 2=2a+ =2a+ =2a﹣ =2a﹣1+ =2[(a+1)+ ]﹣3,
ω μ
∵a (﹣ ,1),∴a+1>0,
∈
∴(a+1)+ ≥2 =2,当且仅当a+1= ,即a=0时取等号,
即 ﹣ 2=2[(a+1)+ ]﹣3≥2×2﹣3=1,
即 ﹣ 2的最小值为1
ω μ
【知识点】复数的运算
ω μ
21.如图,直三棱柱ABC ﹣ABC中,AB=AC=1, ,AA=4,点M为线段AA的中点.
1 1 1 1 1
(1)求直三棱柱ABC ﹣ABC的体积;
1 1 1
(2)求异面直线BM与BC 所成的角的大小.(结果用反三角表示)
1 1【分析】(1)由V=S •AA,即可得解;
△ABC 1
(2)易知∠MBC或其补角即为所求,再在△MBC中,由余弦定理求得cos∠MBC的值,即可.
【解答】解:(1)∵ ,
∴V=S •AA= ×4=2.
△ABC 1
(2)∵BC∥BC ,
1 1
∴∠MBC或其补角是异面直线BM与BC 所成的角,
1 1
在△MBC中,BM=CM= ,BC= ,
由余弦定理得,cos∠MBC= = ,
∴∠MBC=arccos ,
故异面直线BM与BC 所成的角为 .
1 1
【知识点】棱柱、棱锥、棱台的体积、异面直线及其所成的角
22.如图所示,在正方体ABCD﹣ABC D 中,点G在棱DC 上,且DG= DC ,点E、F、M分别是棱
1 1 1 1 1 1 1 1 1
AA、AB、BC的中点,P为线段BD上一点,AB=4.
1 1
(Ⅰ)若平面EFP交平面DCC D 于直线l,求证:l∥AB;
1 1 1
(Ⅱ)若直线BD⊥平面EFP.
1
(i)求三棱锥B﹣EFP的表面积;
1
(ii)试作出平面EGM与正方体ABCD﹣ABC D 各个面的交线,并写出作图步骤,保留作图痕迹.设平
1 1 1 1
面EGM与棱AD 交于点Q,求三棱锥Q﹣EFP的体积.
1 1【分析】(1)根据面面平行的性质即可得到EF∥l,再结合线线平行的传递性即可证明结论;
(2)(i)先根据直线BD⊥平面EFP得到BD⊥EP,进而得到P是DB 的中点,然后依次求
1 1 1
出三棱锥的四个面的面积再相加即可得到三棱锥B﹣EFP的表面积;
1
(ii)①根据公理“一条直线上的两点在一个平面内,那么这条直线在此平面内”作出平面
EGM与正方体ABCD﹣ABC D 各个面的交线即可;②根据NEFP四点共面,且三角形PNE
1 1 1 1
与三角形PEF面积相等,那么三棱锥Q﹣EFP的体积等于三棱锥P﹣ENQ的体积,直接利用
三棱锥的体积公式求解即可.
【解答】解:(1)在正方体ABCD﹣ABC D 中,
1 1 1 1
因为平面ABBA∥平面 DCC D,平面EFP∩平面 ABBA=EF,
1 1 1 1 1 1
所以EF∥l,
因为点E、F 分别是棱 AA、AB 的中点,
1
所以 EF∥AB,
1
所以l∥AB.
1
(2)(i)因为直线 BD⊥平面 EFP,EP 平面 EFP,
1
所以 BD⊥EP,又因为△DAE≌△BAE,
1 1 1
⊂
所以DE=BE,
1
所以DP=BP,
1
因为 ,
× ,
,
所以三棱锥B﹣EFP的表面积为 .
1
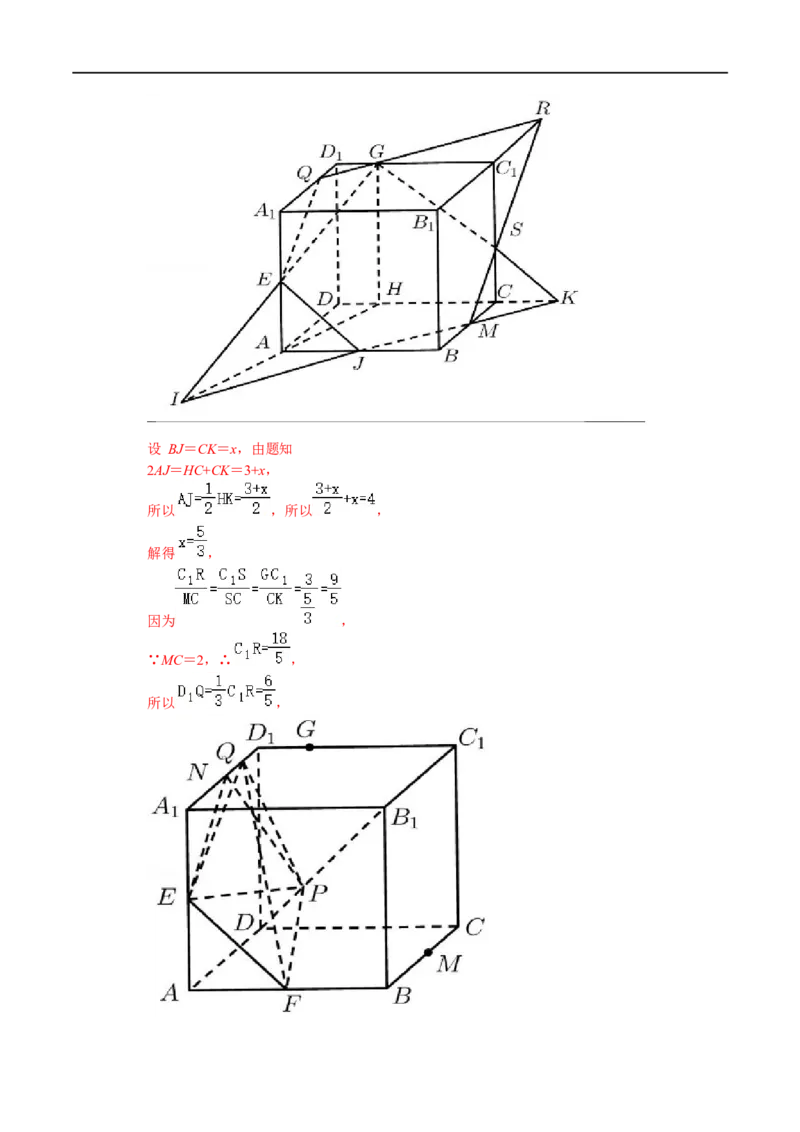
(ii)作图步骤如下:
连接GE,过点G作GH⊥DC于点H,连接HA并延长交GE的延长线于点I,连接IM并延长
交AB于点J交DC的延长线于点K,
再连接GK交CC 于点S,连接MS并延长交BC 的延长线于点R,连接RG并延长交AD 于点
1 1 1 1 1
Q,再连接EQ,GS,EJ,
则图中EQ,QG,GS,SM,MJ,JE即为平面EGM与正方体各个面的交线.设 BJ=CK=x,由题知
2AJ=HC+CK=3+x,
所以 ,所以 ,
解得 ,
因为 ,
∵MC=2,∴ ,
所以 ,如上图,设N为线段AD 的中点,可证点N在平面PEF内,且三角形PNE与三角形PEF面积
1 1
相等,
所以,三棱锥 Q﹣EFP 的体积=三棱锥 Q﹣ENP 的体积=三棱锥 P﹣ENQ 的体积=
,
所以三棱锥Q﹣EFP 的体积为 .
【知识点】平面与平面垂直、棱柱、棱锥、棱台的体积、棱柱、棱锥、棱台的侧面积和表面积