文档内容
2.6.2 双曲线的几何性质(1) -B提高练
一、选择题
1. (2020·安徽无为中学高二期末)设双曲线 的渐近线方程为 ,则
的值为( )
A.4 B.3 C.2 D.1
【答案】C
【解析】由双曲线的几何性质可得,双曲线 的渐近线方程为 ,又因为
渐近线方程为 ,即 ,故 ,选C.
2.(2020山东泰安一中高二月考)若双曲线 的焦距等于10,则实数m的值等于(
)
A.20 B. C. D.
【答案】C
【解析】当 时,方程化为 ,双曲线的焦点在x轴上,则 ,依题
意有 ,解得 ;当 时,方程化为 ,双曲线的焦点在y轴
上,则 ,依题意有 ,解得 .综上, .故选:
C
3.(2020·沙坪坝重庆八中期中)已知双曲线 的离心率为 ,焦点到渐近线距离为 ,则双曲线 实轴长( )
A. B. C. D.
【答案】D
【解析】由题意,双曲线的一个渐近线为 即 ,
设双曲线的的右焦点为 ,则 ,所以焦点到渐近线的距离
,又离心率 ,所以 ,所以双曲线 实轴长 .
x2 y2 y2 x2
4.(2020大连二四中高二月考)我们把方程分别为 - =1和 - =1的双曲线称为共轭双曲
a2 b2 b2 a2
线,则共轭双曲线有相同的( )
A.离心率 B.渐近线 C.焦点 D.顶点
【答案】B
【解析】共轭双曲线 x2 y2 =1 和 y2 x2 =1 的 c= ,设 a>0,b>0,可得它们的焦点分别为
- - √a2+b2
a2 b2 b2 a2
b c c
(±c,0),(0,±c),渐近线方程均为y=± x,离心率分别为 和 ,它们的顶点分别为(±a,0),(0,±b).
a a b
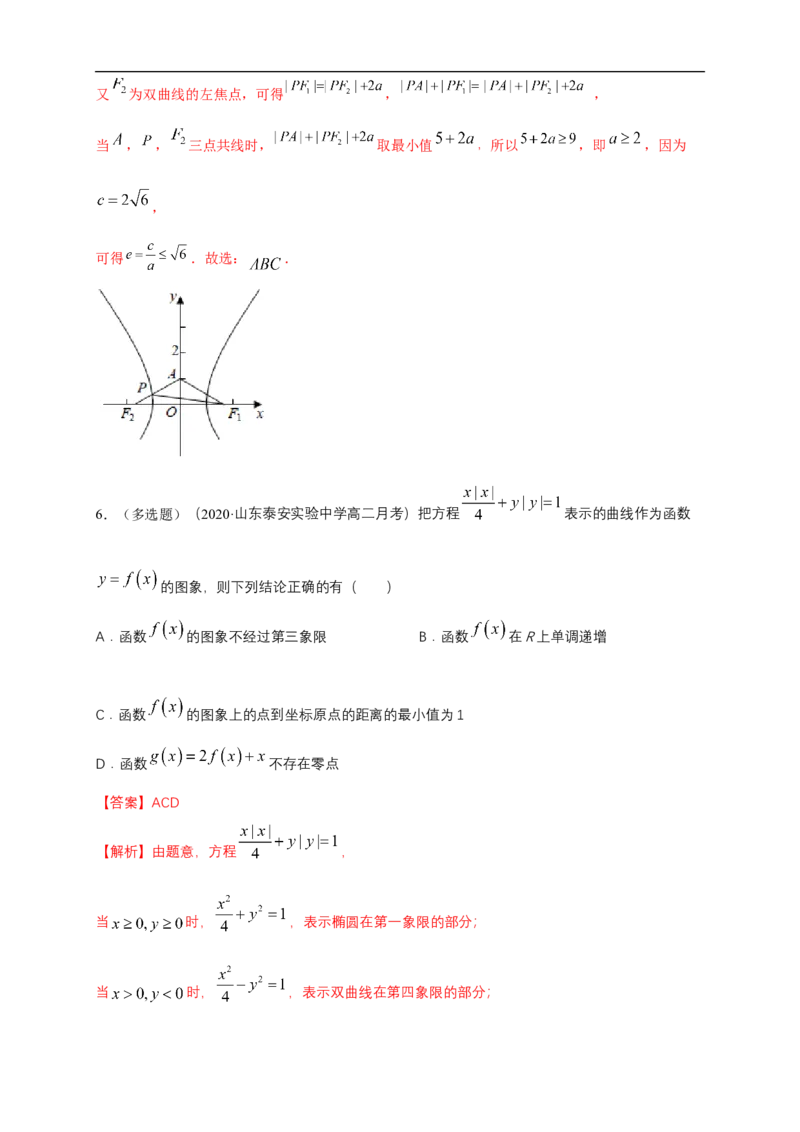
5. (多选题)(2020·南京市天印高级中学高二月考)已知双曲线 的右焦点
为 ,点A坐标为 ,点P双曲线左支上的动点,且 的周长不小于14,则双
曲线C的离心率可能为( )
A. B.2 C. D.3
【答案】ABC
【解析】由右焦点为 ,点 的坐标为 , ,
的周长不小于14,即周长的最小值不小于14,可得 的最小值不小于 9又 为双曲线的左焦点,可得 , ,
当 , , 三点共线时, 取最小值 ,所以 ,即 ,因为
,
可得 .故选: .
6.(多选题)(2020·山东泰安实验中学高二月考)把方程 表示的曲线作为函数
的图象,则下列结论正确的有( )
A.函数 的图象不经过第三象限 B.函数 在R上单调递增
C.函数 的图象上的点到坐标原点的距离的最小值为1
D.函数 不存在零点
【答案】ACD
【解析】由题意,方程 ,
当 时, ,表示椭圆在第一象限的部分;
当 时, ,表示双曲线在第四象限的部分;当 时, ,表示双曲线在第二象限的部分;
当 时, ,此时不成立,舍去,其图像如图所示,可得该函数的图象不经
过第三象限,所以A是正确的;由函数的图象可得,该函数在 为单调递减函数,所以B不正确;
由图象可得,函数 的图象上的点 到原点的距离的最小的点在 的图象上,
设点 ,则点 满足 时, ,即
则 ,当 时, ,所以C正确;
令 ,可得 ,即 ,
则函数 的零点,即为函数 与 的交点,
又由直线 为双曲线 和 渐近线,
所以直线 与函数 没有交点,即函数 不存在零点,
所以D是正确的.故选:ACD.
二、填空题7.已知双曲线 的虚轴长是实轴长的2倍,则双曲线的标准方程为_________.
【答案】
【解析】由题意可得: ,则实轴长为: ,虚轴长为 ,
由题意有: ,解得: ,代入 可得双曲线方程为
.
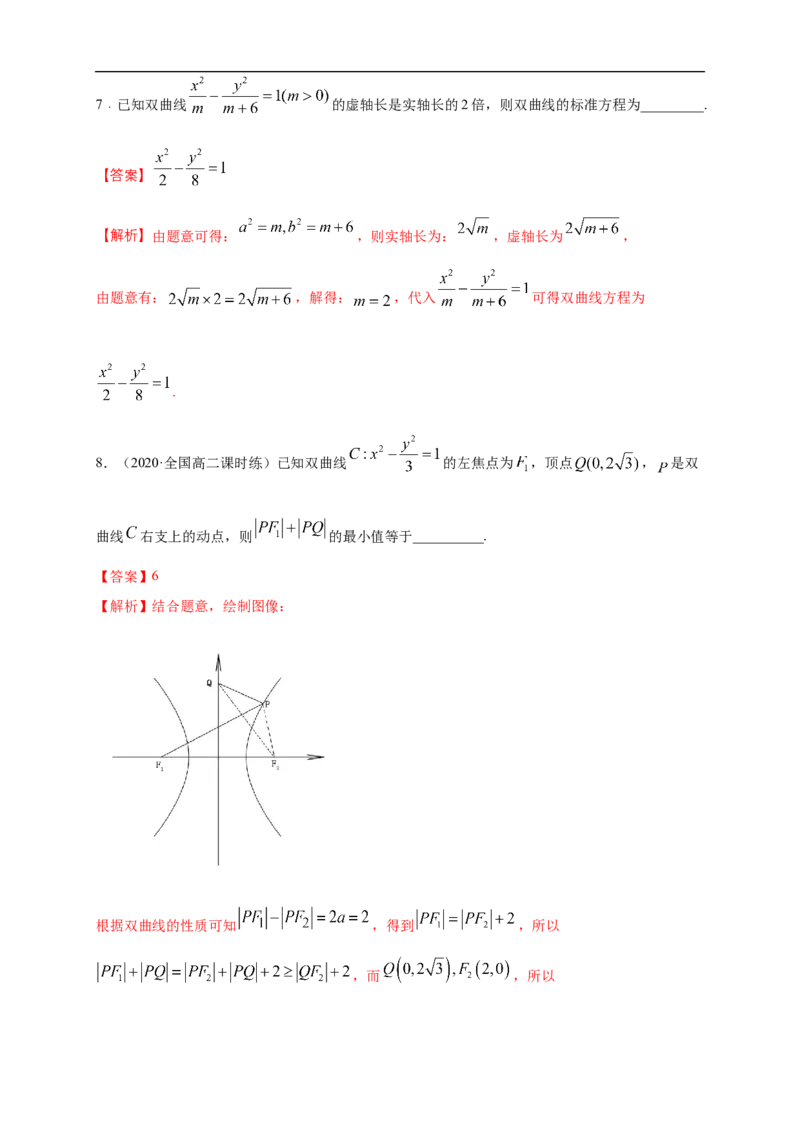
8.(2020·全国高二课时练)已知双曲线 的左焦点为 ,顶点 , 是双
曲线 右支上的动点,则 的最小值等于__________.
【答案】6
【解析】结合题意,绘制图像:
根据双曲线的性质可知 ,得到 ,所以
,而 ,所以,所以最小值为6.
x2 y2
9.(2019全国高考)双曲线C: - =1的右焦点为F,点P在C的一条渐近线上,O为坐标原点.若|PO|
4 2
=|PF|,则△PFO的面积为__________.
3√2
【答案】
4
【解析】由已知可得a=2,b= ,则c= ,∴F( ,0).
√2 √a2+b2=√6 √6
√6 √2 √2 √6 √3
∵|PO|=|PF|,∴x = .又P在C的一条渐近线上,不妨设在渐近线y= x上,∴y = × = .
P P
2 2 2 2 2
1 1 √3 3√2
∴S = |OF|·|y |= ×√6× = .
△PFO 2 P 2 2 4
10. (2020·山东潍坊三中高二月考)设双曲线 , , 是双曲线 上
关于坐标原点对称的两点, 为双曲线 上的一动点,若 ,则双曲线 的离心率为
__________.
【答案】
【解析】由题意,设 , ,则 ,所以
,因为 , ,
所以两式相减可得 ,即 ,
因为 ,所以 ,则 .
三、解答题
11. (2020·江苏省如皋中学高二月考)已知双曲线的中心在原点,焦点 , 在坐标轴上,离心率为 ,且过点 ,
(1)求双曲线的方程;
(2)若点 为 轴上一定点, 为双曲线右支上一点,求线段 长的最小值.
【解析】(1)因为 ,则双曲线的实轴、虚轴相等
所以可设双曲线方程为
因为双曲线过点(4, ),所以 ,即
所以双曲线方程为
(2)设 ,
令
①当 即 时,当 时, ,
②当 即 时,当 时, ,
12.(2020·全国高二课时练)已知双曲线过点(3,-2)且与椭圆4x2+9y2=36有相同的焦点.
(1)求双曲线的标准方程;
(2)若点M在双曲线上,F,F 为左、右焦点,且|MF |+|MF |=6 ,试判别△MF F 的形状.
1 2 1 2 1 2
【解析】 (1)椭圆方程可化为 ,焦点在x轴上,且c= ,
故设双曲线方程为 ,
则有 解得a2=3,b2=2.所以双曲线的标准方程为 .
(2)不妨设M点在右支上,
则有|MF |-|MF |=2 ,又|MF |+|MF |=6 ,
1 2 1 2
故解得|MF |=4 ,|MF |=2 ,又|FF|=2 ,
1 2 1 2
因此在△MF F 中,|MF |边最长,而
1 2 1
cos ∠MF F= ,
2 1
所以∠MF F 为钝角,故△MF F 为钝角三角形.
2 1 1 2