文档内容
格致课堂
7.3.2 复数的三角形式乘、除运算的三角表示及其几何意义
(用时45分钟)
【选题明细表】
知识点、方法 题号
复数的三角形式乘、除运算 1,2,3,5,6,8,9
复数的三角形式乘、除运算的几何意义 4,7,10,11,12
基础巩固
1.已知i为虚数单位, , ,则 ( )
A. B.
C. D.
【答案】D
【解析】 ,
.
故选:D.
2. ( )
A. B. C. D.
【答案】B
【解析】
.
故选:B.格致课堂
3.计算 的结果是( )
A.-9 B.9 C.-1 D.1
【答案】B
【解析】
,
故选:B.
4.将复数 对应的向量 绕原点按顺时针方向旋转 ,得到的向量为 ,那么 对应的复
数是( )
A. B. C. D.
【答案】A
【解析】复数 的三角形式是 ,向量 对应的复数是
故选:A
5. ( )
A. B. C. D.
【答案】C格致课堂
【解析】
.
故选:C.
6.复数 的代数形式是_____________.
【答案】
【解析】 .
故答案为: .
7.在复平面内,把与复数 对应的向量绕原点 按逆时针方向旋转45°,所得向量对应的复数为 ,则
复数 是_____________.(用代数形式表示).
【答案】
【解析】由题意得 .
8.计算下列各式,并作出几何解释:格致课堂
(1)
(2)
(3)
(4) .
【答案】(1)-4,几何解释见解析 (2) ,几何解释见解析 (3) ,
几何解释见解析 (4) ,几何解释见解析
【解析】(1)原式 .
几何解释:设 ,
作与 对应的向量 ,然后把向量
绕原点O按逆时针方向旋转 ,再将其长度伸长
为原来的 倍,得到一个长度为4,辐角为π的
向量 ,则 即为积 所对应的向量.
(2)原式格致课堂
.
几何解释:设 ,
作与 对应的向量 ,然后把向量
绕原点O按逆时针方向旋转315°,再将其长度缩短
为原来的 ,得到一个长度为 、辐角为 的
向量 ,则 即为积 所对应的向量.
(3)原式
.
几何解释:设 , 作与
对应的向量 ,
然后把向量 绕原点0按顺时针方向旋转 ,再将其长度
缩短为原来的 ,得到一个长度为 ,辐角为 的向量 ,
则 即为 所对应的向量.格致课堂
(4)原式
.
几何解释:设 ,
作与 对应的向量 ,然后把向量
绕原点0按顺时针方向旋转 ,再将其长度缩短为原来的 ,
得到一个长度为 ,辐角为 的向量 ,
则 即为 所对应的向量.
能力提升
9.复数 是方程 的一个根,那么 的值等于( )
A. B. C. D.
【答案】B
【解析】由题意得,
故选:B
10.设 对应的向量为 ,将 绕原点按顺时针方向旋转 所得向量对应的复数的虚部为
________.
【答案】格致课堂
【解析】所得向量对应的复数为
,故虚部为 ,
故答案为: .
11.把复数 与 对应的向量 , 分别按逆时针方向旋转 和 后,与向量 重合且模相等,
已知 ,求复数 的代数式和它的辐角主值.
【答案】 ,
【解析】由复数乘法的几何意义得 ,
又
的辐角主值为
素养达成
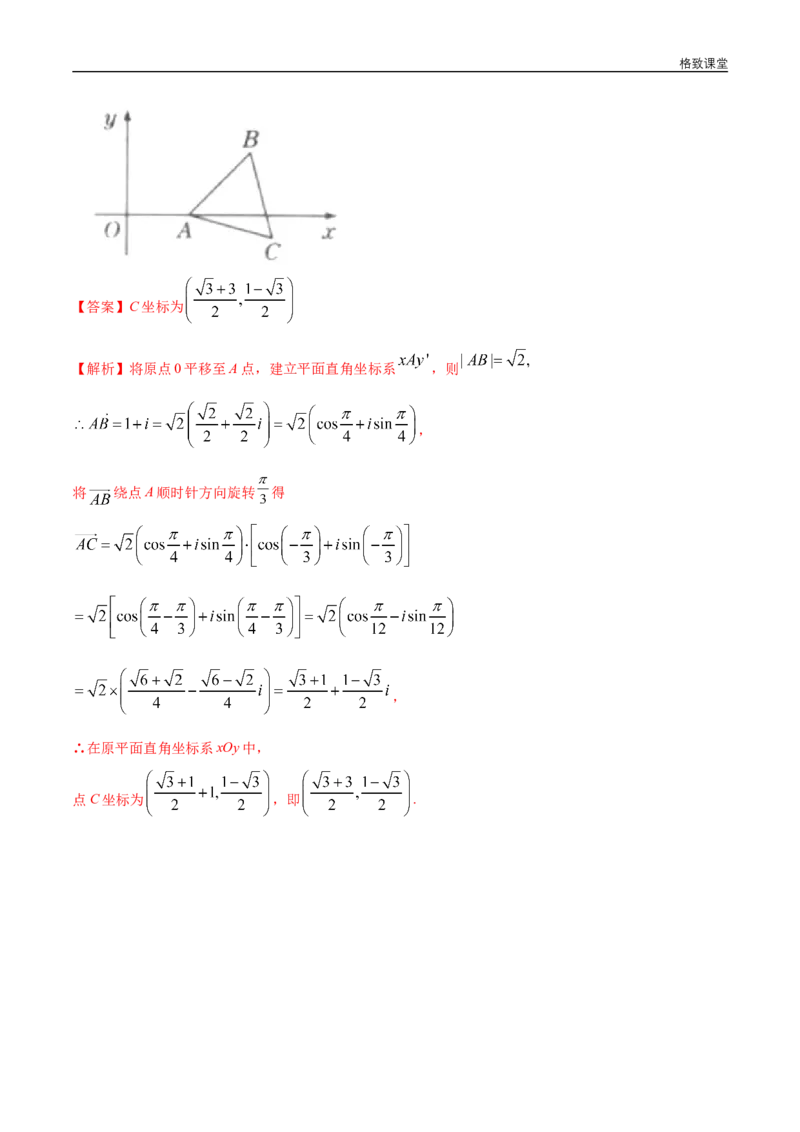
12.如图,复平面内的是△ABC等边三角形,它的两个顶点A,B的坐标分别为 ,求点C的坐
标.格致课堂
【答案】C坐标为
【解析】将原点0平移至A点,建立平面直角坐标系 ,则
,
将 绕点A顺时针方向旋转 得
,
∴在原平面直角坐标系xOy中,
点C坐标为 ,即 .