文档内容
格致课堂
8.4.1 平面
一、选择题
1.下列命题正确的是( )
A.经过三点确定一个平面
B.经过一条直线和一个点确定一个平面
C.两两相交且不共点的三条直线确定一个平面
D.四边形确定一个平面
【答案】C
【解析】
A选项,根据平面基本性质知,不共线的三点确定一个平面,故错误;B选项,根据平面基本性质公理一
的推论,直线和直线外一点确定一个平面,故错误;C选项,根据公理一可知,不共线的三点确定一个平
面,而两两相交且不共点的三条直线,在三个不共线的交点确定的唯一平面内,所以两两相交且不共点的
三条直线确定一个平面,正确;选项D,空间四边形不能确定一个平面,故错误;综上知选C.
2.如果直线a 平面α,直线b 平面α, ,且 ,那么( )
⊂ ⊂
A. B.
C. D.
【答案】A
【解析】∵直线a 平面α,直线b 平面α,M∈a,N∈b,
∴M∈平面α,N∈⊂平面α, ⊂
∵M∈l,N∈l,
∴l α.
故选⊂A.
3. 下列命题中,正确的是 ( )
A.经过正方体任意两条面对角线,有且只有一个平面
B.经过正方体任意两条体对角线,有且只有一个平面
C.经过正方体任意两条棱,有且只有一个平面
D.经过正方体任意一条体对角线与任意一条面对角线,有且只有一个平面
【答案】B格致课堂
【解析】
因为正方体的四条体对角线相交于同一点(正方体的中心),因此经过正方体任意两条体对角线,有且只有
一个平面,故选B.
4.在空间四边形ABCD的边AB,BC,CD,DA上分别取E、F、G、H四点,如果EF,GH交于一点P,
则( )
A.P一定在直线BD上
B.P一定在直线AC上
C.P一定在直线AC或BD上
D.P既不在直线AC上,也不在直线BD上
【答案】B
【解析】EF、GH相交于点P,
则点P属于直线EF,且属于直线GH.
又由题意,EF属于面ABC,GH属于面ADC
则点P即属于面ABC,又属于面ADC
则点P必在面ABC与面ADC的交线上,即
点P必在AC上.故选B.
5.(多选题)下面说法中(其中A,B表示点,a表示直线,α表示平面):
A.因为A α,B α,所以AB α;
B.因为A∈⊂α,B⊂∈α,所以AB⊂∈α;
C.因为A a,a α,所以A α;
D.因为A∉α,a⊂α,所以A∉a.
其中错误∉的说法⊂是 ( )∉
【答案】ABC
【解析】点在平面上,用“∈”表示,不能用“⊂”表示,故不正确;AB在α内,用“⊂”表示,不能用
“∈”表示,故B不正确;由A a,a α,不能得出A α,故C不正确;由A α,a α,知A a,故D正
确. 选ABC. ∉ ⊂ ∉ ∉ ⊂ ∉
6.(多选题)如图,α∩β=l,A∈α,C∈β,C l,直线AD∩l=D,A,B,C三点确定的平面为γ,则平
面γ、β的交线必过( ) ∉格致课堂
A.点A B.点B
C.点C D.点D
【答案】CD
【解析】
A、B、C确定的平面γ与直线BD和点C确定的平面重合,故C、D∈γ,又C、D∈β,故C,D在γ和β
的交线上.故选CD。
二、填空题
7. 若直线l与平面α相交于点O、A、B∈l、C、D∈α,且AC∥BD,则O、C、D三点的位置关系是
____.
【答案】共线
【解析】如图,因为AC∥BD,所以AC与BD确定一个平面,记为β,
则α∩β=CD,
因为l∩α=O,所以O∈α,又O∈AB β,所以O∈β,所以O∈CD.故O,C,D共线.
8.如图所示,A,B,C,D为不共面⊂的四点,E,F,G,H分别在线段AB,BC,CD,DA上.如果
EF∩GH=Q,那么Q在直线________上.
【答案】AC格致课堂
【解析】
若EF∩GH=Q,则点Q∈平面ABC,Q∈平面ACD.而平面ABC∩平面ACD=AC,所以Q∈AC.
答案:AC
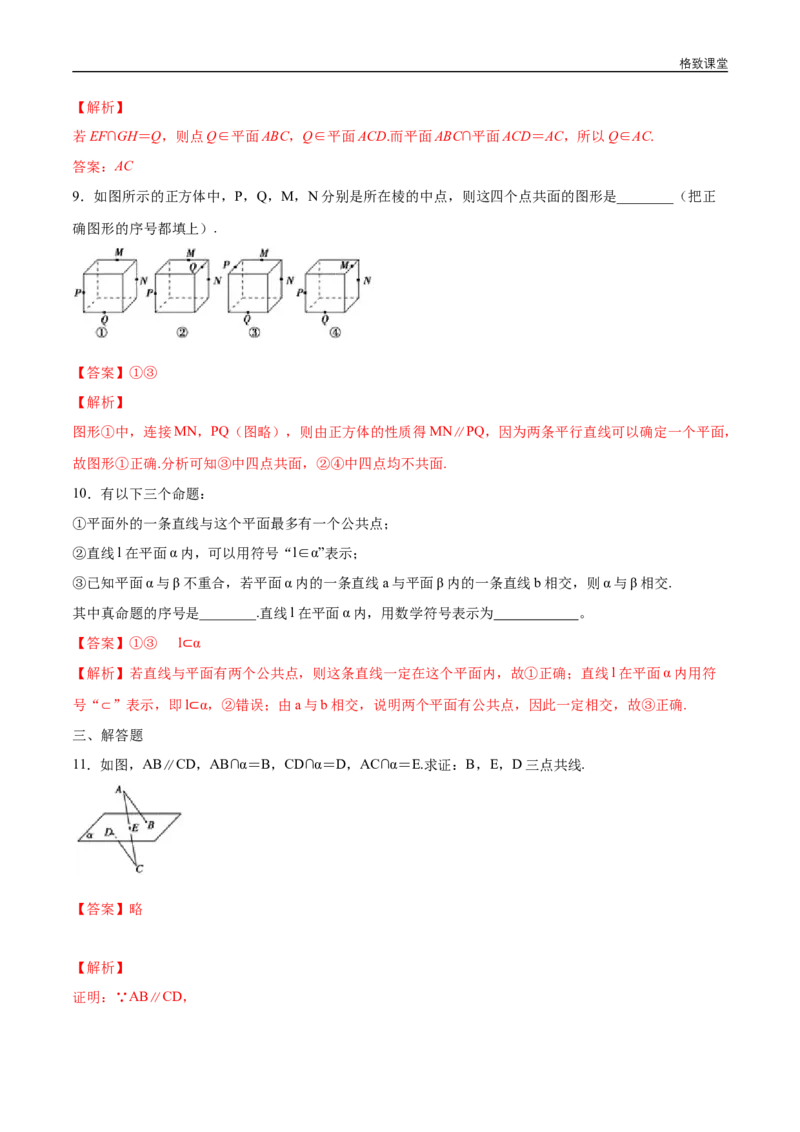
9.如图所示的正方体中,P,Q,M,N分别是所在棱的中点,则这四个点共面的图形是________(把正
确图形的序号都填上).
【答案】①③
【解析】
图形①中,连接MN,PQ(图略),则由正方体的性质得MN∥PQ,因为两条平行直线可以确定一个平面,
故图形①正确.分析可知③中四点共面,②④中四点均不共面.
10.有以下三个命题:
①平面外的一条直线与这个平面最多有一个公共点;
②直线l在平面α内,可以用符号“l∈α”表示;
③已知平面α与β不重合,若平面α内的一条直线a与平面β内的一条直线b相交,则α与β相交.
其中真命题的序号是________.直线l在平面α内,用数学符号表示为 。
【答案】①③ l α
【解析】若直线与⊂平面有两个公共点,则这条直线一定在这个平面内,故①正确;直线l在平面α内用符
号“⊂”表示,即l α,②错误;由a与b相交,说明两个平面有公共点,因此一定相交,故③正确.
三、解答题 ⊂
11.如图,AB∥CD,AB∩α=B,CD∩α=D,AC∩α=E.求证:B,E,D三点共线.
【答案】略
【解析】
证明:∵AB∥CD,格致课堂
∴AB,CD可确定一个平面,设为平面β,
∴AC在平面β内,即E在平面β内.
而AB∩α=B,CD∩α=D,AC∩α=E,
可知B,D,E为平面α与平面β的公共点,
根据公理3可得,B,D,E三点共线.
12.已知:a、b、c、d是不共点且两两相交的四条直线,求证:a、b、c、d共面
【答案】见解析
【解析】
证法1:若当四条直线中有三条相交于一点,不妨设a、b、c相交于一点A,∴直线d和A确定一个平面α.
又设直线d与a、b、c分别相交于E、F、G,则A、E、F、G∈α.∵A、E∈α,A、E∈a,∴aα.同理可证
b α,c α.∴a、b、c、d在同一平面α内.
证法2:当四条直线中任何三条都不共点时,如图.∵这四条直线两两相交,则设相交直线a、b确定一个
平面α.设直线c与a、b分别交于点H、K,则H、K∈α.又H、K∈c,∴c α.同理可证d α.∴a、b、c、d
四条直线在同一平面α内.